אשכול פרספקטיבה – חלק ב – כיצד מסרטטים תיבה בפרספקטיבה – למורה
הנחיות למורה
אשכול מס' 2 מתוך 5 אשכולות.
יחידה:
אמנות
כיתה מומלצת:
כיתה ז – כיתה י
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (קונטקסט):
- הכרת טכניקת אמנות ליצירת אשליה של תלת-ממד על משטח דו-ממדי, הנקראת פרספקטיבה ומושגים העיקריים (קו אופק, נקודת מגוז).
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| מצבים הדדיים בין ישרים: ניצבות והקבלה | – ישרים מקבילים – ישרים מאונכים | – זיהוי וסרטוט של ישרים מקבילים וישרים מאונכים המכילים צלעות של תיבה. |
| תיבה | – פאה, מקצוע, קודקוד – ממדי תיבה | – זיהוי מושגים עיקריים של תיבה. – דרגות חופש בבניית תיבה. – ראיה מרחבית. |
מטרות האשכול
- לסרטט תיבה לפי חוקי פרספקטיבה.
- לדון בדרגות החופש של ה"תוצר":
- האם קיימת תיבה נוספת שהמלבן הנתון מהווה הפאה הקדמית שלה?
- האם שינוי מיקום המלבן שמהווה הפאה הקדמית שלה (למשל מעל / מתחת לקו האופק) גורם לשינוי בתיבה?
תפקיד המדרגות
בכל מדרגה נתון סרטוט חלקי של תיבה שכולל את קו האופק, נקודת המגוז, מלבן המייצג פאה קדמית של תיבה וקווים מקבילים שעשויים לשמש כ"אבן הבניה" של הפאות הגלויות לעין של התיבה. התלמידים מתבקשים להשלים תיבה ועשויים אף להבחין בדרגות החופש בסרטוט התיבה.
שימו לב:
בבעיות המופיעות בכל אחת מהמדרגות, הכוונה שתלמידים מסרטטים את פאות התיבה שניתן לראות בעין.
בנוסף, גם הצופה וגם התיבה בשלב זה במצב סטטי.
שלב הלמידה המומלץ
- כיתה ז לאחר למידת הנושא "תיבה".
- כיתה ח אפשר לאחר למידת הנושא דמיון משולשים (במידה ותרצו להמשיך עם אשכולות הבאים ולחשוף את התלמידים לאשכול ג).
- כיתות ט-י בכל שלב של למידה.
ארגון כיתה מומלץ
- למידה בזוגות או בקבוצות.
- מומלץ לפתוח את השיעור בצפייה בסרטון המתייחס למושגים עיקריים של פרספקטיבה חד מגוזית ומסביר כיצד מסרטטים תיבה לפי עקרונות הפרספקטיבה.
מומלץ לערוך דיון קצר סביב הדברים שעלו בסרטון מבחינת המושגים של הפרספקטיבה. לפי שיקול דעת של המורה אם להתייחס בדיון למושגים גיאומטריים הקשורים לתיבה (ללא בניה עצמה). - המורה יאפשר לתלמידים לענות על השאלות באשכול באופן עצמאי, כשהם יכולים להיעזר במדרגות וביישומונים.
המורה יעודד תלמידים שמתקשים להיעזר במדרגות, לשתף פעולה, ולהדריך את התלמידים במקרה שישנן אי הבנות. - המורה יערוך דיון כיתתי, סביב השאלות שעלו במהלך הפתרון של השאלות באשכול.
לפי שיקול דעת של המורה אם כדאי לערוך דיוני ביניים במידה ומזהה קושי.
שאלות מומלצות לדיון כיתתי
- תארו את התהליך של סרטוט התיבה שלכם.
כיצד עקרונות של פרספקטיבה חד מגוזית באים לידי ביטוי בתיבה שסרטטתם? - תארו אילו צלעות, פאות, קודקודים ניתן לראות בתיבה שסרטטתם? סמנו אותן.
כיצד לדעתכם ניתן למקם את המלבן המייצג את הפאה הקדמית של התיבה כך שניתן יהיה לראות רק פאה אחת של תיבה? שתי פאות תיבה? שלוש פאות תיבה?
האם שינוי של מיקום תיבה (הזזה אופקית / אנכית) גורם לכך שנוצרת תיבה אחרת? - באילו נתונים תתקבל תיבה יחידה?
סרטונים לשילוב בשיעור
מומלץ לצפות בסרטון.
אשכול פרספקטיבה – חלק ב – כיצד מסרטטים תיבה בפרספקטיבה
פרספקטיבה בצילום ובסרטוט
אנחנו חיים בעולם תלת-ממדי, אך כאשר רוצים לתאר אותו בציור או בצילום אנחנו עושים את זה בדפים דו-ממדיים. הדרך לייצג אובייקטים תלת ממדיים על משטח דו-ממדי, כמו בציור או בסרטוטים אדריכליים, נקראת פרספקטיבה.
באשכול א הכרתם את המושגים העיקריים של פרספקטיבה.
באשכולות הבאים תסרטטו בעצמכם את האובייקטים התלת-ממדיים בדו-מימד ותלמדו כיצד מתמטיקה שלמדתם בבית הספר עוזרת להבין את יחסי הגומלין בין המרכיבים השונים של האובייקטים (אורכים, מקבילות, מאונכות וכו').
פסי הרכבת מקבילים במציאות והאדנים מונחים בניצב לכיוון הפסים ומחברים ביניהם, כך שהמרחק בין הפסים נשמר קבוע לכל אורך המסילה. אולם, כשאנחנו מסתכלים על פסי הרכבת בתמונה, הם נתפשים על ידי העין כקווים נחתכים ונראה שהמרחק בין הפסים קטן וכך גם קטן האורך של כל אדן, אבל האדנים נשארים מקבילים – כך נוצרת אשליית מרחק ועומק. כלומר, הרחוק יותר נראה קטן יותר והקרוב יותר נראה גדול יותר (ראו תמונות שלפניכם)
(ניתן ללחוץ על התמונה ולהגדיל אותה)
כדי לתאר מצב תלת ממדי בדפים דו-ממדיים משתמשים בשיטה המבוססת על העובדה שכל עצם נראה קטן יותר ככל שהוא רחוק יותר מהעין. השיטה נקראת פרספקטיבה (בעברית תִּשְקוֹפֶת). המושג שאוב מהמילה הלטינית perspicere שמשמעה "לראות מבעד", לראות דרך חלון שקוף.
הגדרות
- לכל ציור או צילום יש קו ראיה יחיד שהוא בגובה העיניים של הצייר או הצלם.
קו זה נקרא קו האופק. קו האופק מקביל למסגרת התמונה. - נקודת המָגוֹז או נקודת ההיעלמות היא הנקודה על קו האופק שבה הדברים "נעלמים".
- כל הקווים המקבילים ביניהם שכיוונם לקו האופק מתכנסים בנקודת המגוז. קווים אחרים שמקבילים זה לזה יישארו מקבילים גם בפרספקטיבה. כך נוצרת אשליה של עומק.
- קווים שבמציאות מאונכים, בפרספקטיבה לא יוצרים זווית ישרה. רק הקווים המאונכים לקו האופק נשארים מאונכים לו ולכל קו המקביל לקו האופק.
- עצמים שווים בגודלם במציאות (כמו מבנים, עצים, הרים, אנשים וכו'), ייראו בציור ובצילום קטנים יותר ככל שהם רחוקים יותר. באשכול זה נעסוק בפרספקטיבה חד מָגוֹזית – פרספקטיבה שיש בה נקודת מגוז אחת.
הידעתם? משתמשים בפרספקטיבה בהרבה תחומים: באומנות- ציורים, באדריכלות, בתכנון מבנים , עיצוב פנים וכיום גם בגרפיקה ממוחשבת.
ראו את הסרטון "פרספקטיבה חד מגוזית", וסכמו כיצד עקרונות הפרספקטיבה באים לידי ביטוי בציור של תיבה בסרטון.
1. בעיית מטרה
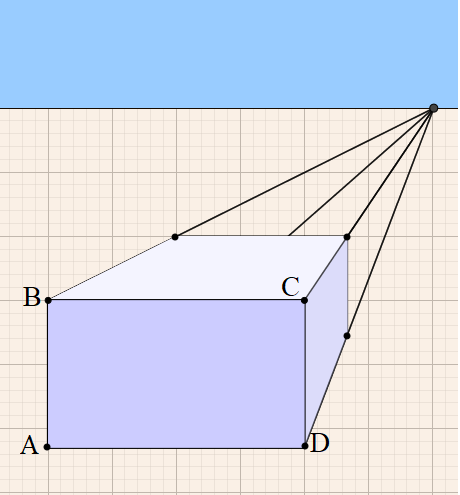
- סרטטו בדף משובץ תיבה בהתבסס על עקרונות הפרספקטיבה באופן הבא:
\(\space\)
1. סרטטו קו אופק וסמנו עליו נקודת מגוז.
\(\space\)
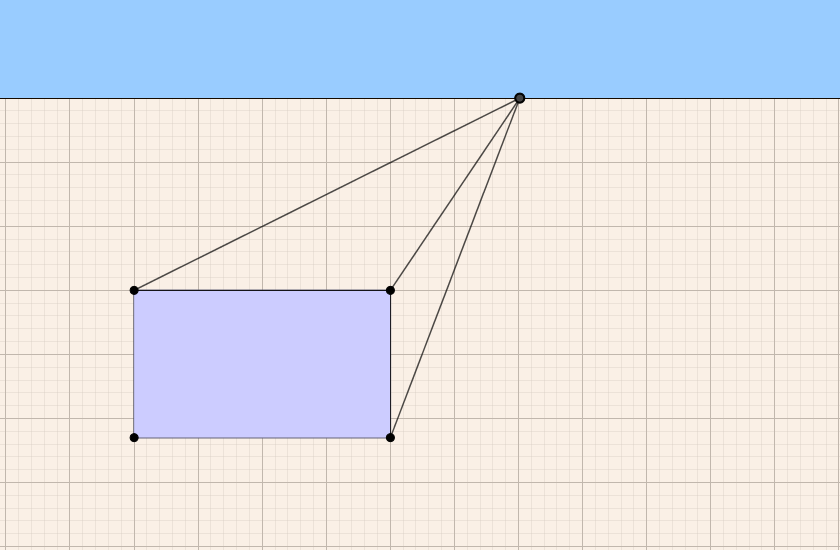
2. סרטטו מתחת לקו האופק מלבן המייצג פאה קדמית של תיבה.
השלימו את התיבה לפי העקרונות של פרספקטיבה.
\(\space\)
3. האם התיבה שסרטטתם היא האפשרות היחידה?
אם כן, נמקו.
אם לא, סרטטו תיבה נוספת.
\(\space\) - סרטטו מלבן נוסף מעל קו האופק והשלימו לתיבה מתאימה.
- אחרי שפתרתם את השאלות בבעיית המטרה, המשיכו לבעיית הסיכום.
- במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון לבעיית המטרה
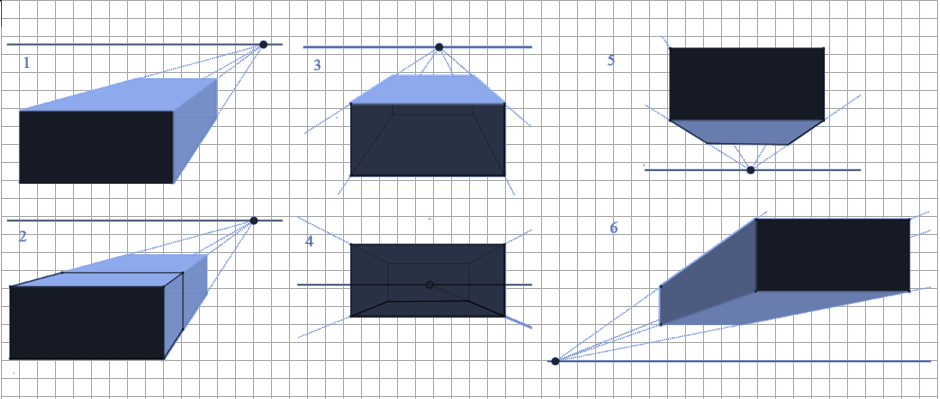
דוגמאות של תיבות המסורטטות בפרספקטיבה חד מגוזית:
המלבן האפור מהווה את הפאה הקדמית של התיבה.
בתרשימים 1, 3-6 מוצגת אותה התיבה (במציאות) למרות שבסרטוט העין שלנו תופשת כל אחת מהתיבות האלה בצורה אחרת.
ואילו בתרשים 2, מוצגת תיבה אחרת, שהתקבלה משינוי הממד השלישי (העומק) של התיבה המקורית (תרשים 1) – תיבה זו שונה מהתיבות האחרות, גם במציאות וגם בסרטוט (בתרשים 2 ניתן לראות גם את התיבה המקורית וגם את התיבה החדשה).
(ניתן ללחוץ על התמונה ולהגדיל אותה)
(ניתן ללחוץ על התמונה ולהגדיל אותה)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית המטרה.
- במידת הצורך, פתרו את השאלות במדרגה 2.
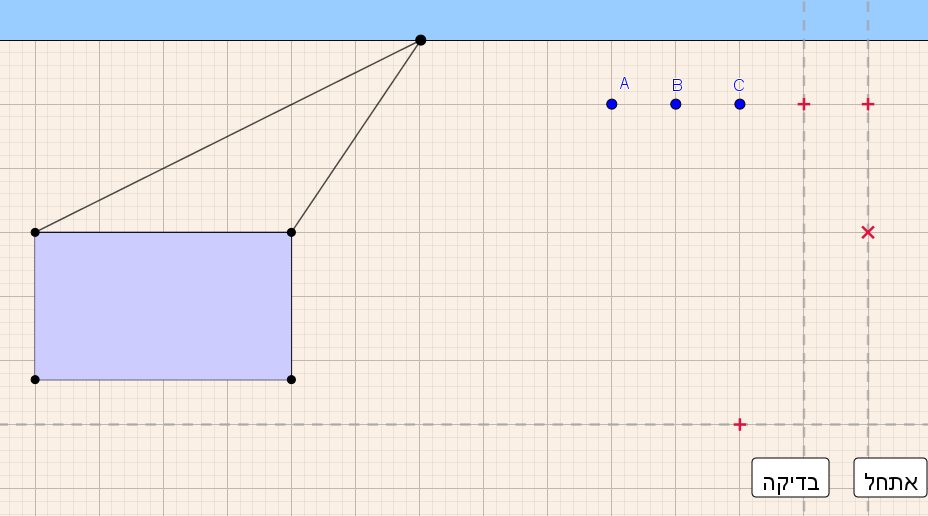
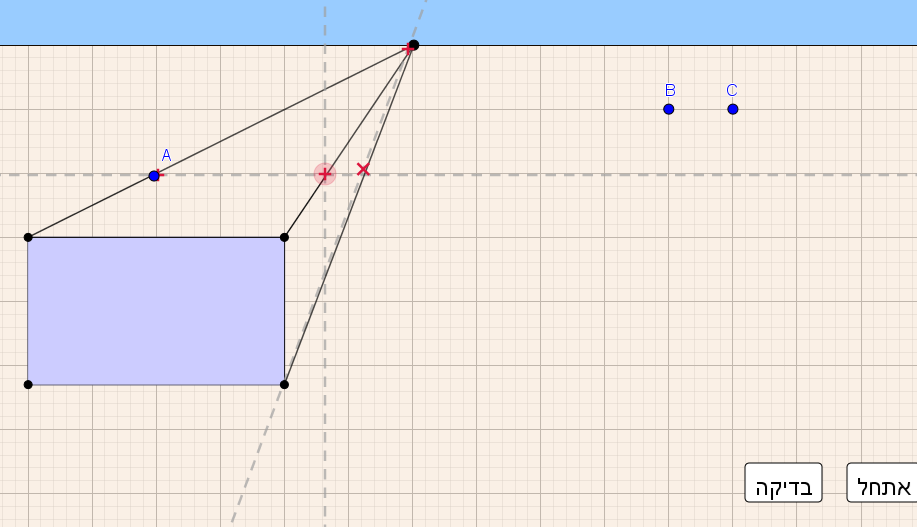
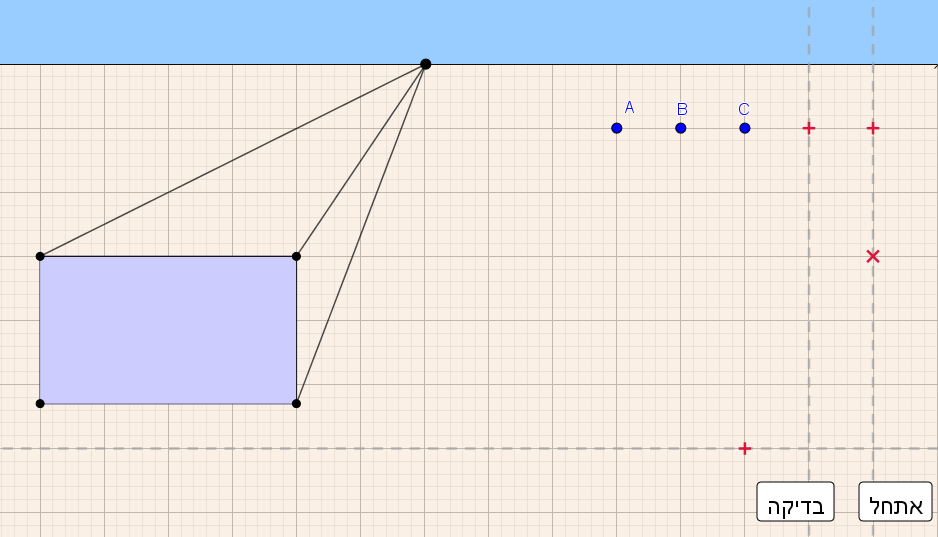
- יש למקם את 3 הנקודות \(A, B, C\) כך שתתקבל תיבה המסורטטת בפרספקטיבה.
- לחצו על כפתור "בדיקה":
אם כל שלוש הנקודות במקום מתאים, צבען ישתנה לירוק, ופאות התיבה יופיעו.
אם הנקודות (כולן או חלקן) במקום שאינו מתאים, צבען ישתנה לאדום. - ניתן להיעזר ב-3 הישרים המנחים: ישר אופקי, ישר אנכי, וישר משופע.
ניתן להזיז ישר: יש למקם את העכבר על סימן ה"+" ולגרור את העכבר אל מיקום הישר הרצוי.
את הישר המשופע ניתן לסובב: יש למקם את העכבר על סימן ה"x", ולגרור את העכבר בזווית השיפוע המבוקשת.
פתרון מדרגה 1
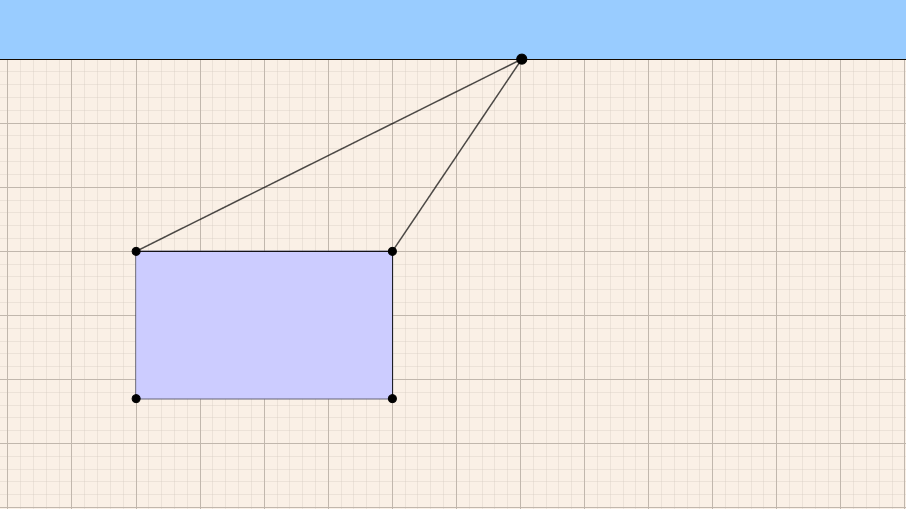
התלמידים מתבקשים להשלים את התיבה לפי העקרונות של פרספקטיבה.
[הכוונה שהתלמידים מסרטטים את פאות התיבה שניתן לראות בעין.
בנוסף, גם הצופה וגם התיבה בשלב זה במצב סטטי].
מצב התחלתי:
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
הגדרה של עומק התיבה על ידי סימון אחת הנקודות על אחד הקווים "המקבילים". למשל, כך:
ניתן להתחיל את הבנייה גם מהעברת הקו "המקביל" השלישי, המחבר את הקודקוד הימני התחתון של הפאה הקדמית עם נקודת המגוז.
השלמת שאר הקודקודים כדי שתתקבל תיבה באמצעות שלושת קווי העזר האפורים.
\(\Downarrow\)
בדיקה:
(במידה והבנייה תקפה בלחיצה על הבדיקה תופיע תיבה. אם הבנייה לא תקפה – יתקבל חיווי האובייקטים בצבע אדום)
מטרות מדרגה 1
- אבני הבניה: מלבן המייצג פאה קדמית של תיבה ושני קווים מקבילים, לסרטוט של הפאה העליונה של התיבה.
(ניתן ללחוץ על התמונה ולהגדיל אותה)
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית המטרה.
- במידת הצורך, פתרו את השאלות במדרגה 3.
- יש למקם את 3 הנקודות \(A, B, C\) כך שתתקבל תיבה המסורטטת בפרספקטיבה.
- לחצו על כפתור "בדיקה":
אם כל שלוש הנקודות במקום מתאים, צבען ישתנה לירוק, ופאות התיבה יופיעו.
אם הנקודות (כולן או חלקן) במקום שאינו מתאים, צבען ישתנה לאדום. - ניתן להיעזר ב-3 הישרים המנחים: ישר אופקי, ישר אנכי, וישר משופע.
ניתן להזיז ישר: יש למקם את העכבר על סימן ה"+" ולגרור את העכבר אל מיקום הישר הרצוי.
את הישר המשופע ניתן לסובב: יש למקם את העכבר על סימן ה"x", ולגרור את העכבר בזווית השיפוע המבוקשת.
פתרון מדרגה 2
התלמידים מתבקשים להשלים את התיבה לפי העקרונות של פרספקטיבה.
[הכוונה שהתלמידים מסרטטים את פאות התיבה שניתן לראות בעין.
בנוסף, גם הצופה וגם התיבה בשלב זה במצב סטטי].
במדרגה זו נתונים:
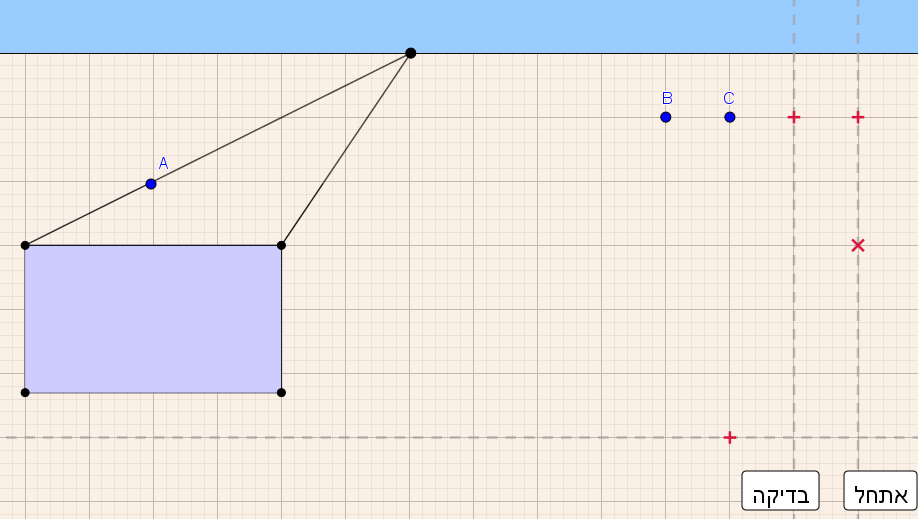
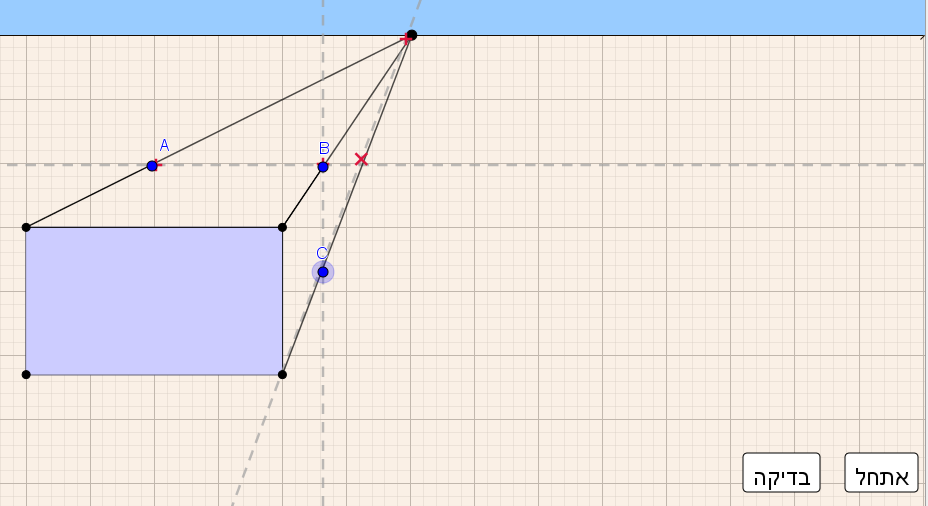
מלבן המייצג פאה קדמית של תיבה, קו אופק, נקודת מגוז ושלושה קוים "מקבילים".
הקו השלישי מוריד את רמת הקושי של הבנייה לעומת מדרגה 1, אך הבנייה עדיין מאתגרת.
על התלמיד לתכנן את סדר הבנייה – להגדיר את עומק התיבה על ידי סימון של אחד הנקודות על אחד הקווים המקבילים ולהשלים את התיבה באמצעות קווי העזר האפורים (בדומה למדרגה 1).
(ניתן ללחוץ על התמונה ולהגדיל אותה)
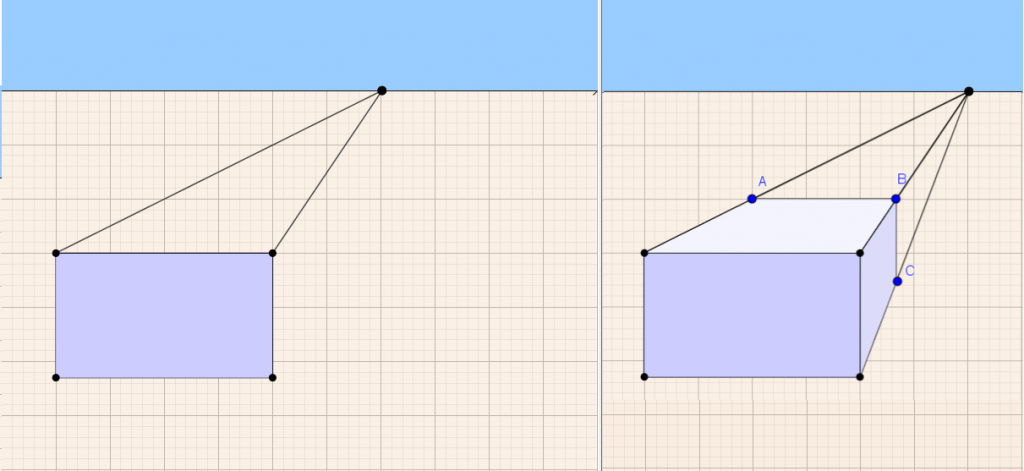
מטרות מדרגה 2
- אבני הבנייה: מלבן המייצג פאה קדמית של תיבה ושלושה קווים מקבילים, לסרטוט של הפאה העליונה של התיבה ופאתה הימנית.
1.3. מדרגה 3 לבעיית המטרה
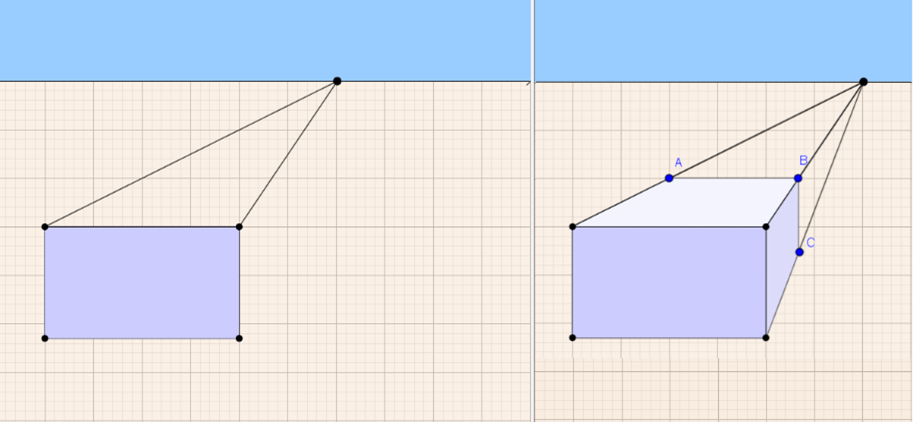
בחלון הימני:
נתונה תיבה המסורטטת לפי העקרונות של פרספקטיבה.
בחלון השמאלי:
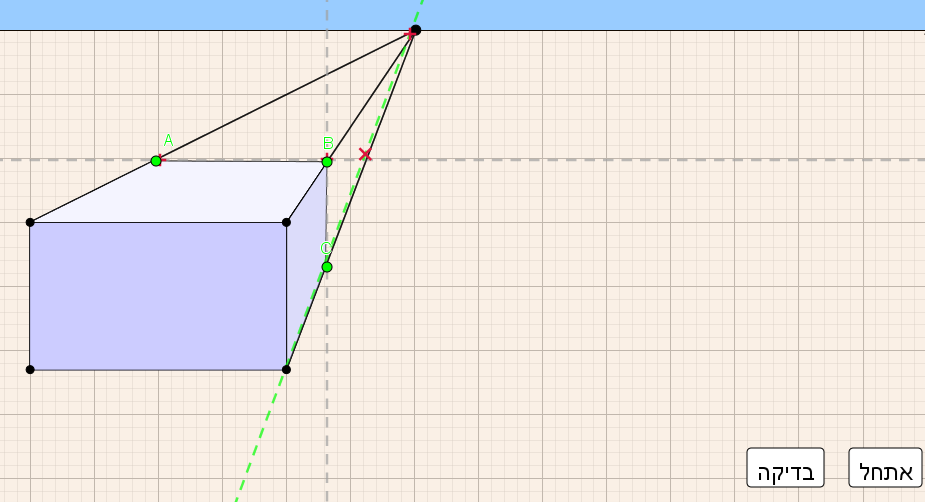
נתונים מלבן המייצג את הפאה הקדמית של התיבה, קו האופק, נקודת מגוז ושני קווים "מקבילים".
השלימו את פאותיה הגלויות לעין (שניתן לראות אותן בעין) של התיבה, לפי העקרונות של פרספקטיבה.
(אפשר להיעזר בתיבה שבחלון מימין ו/או ביישומון).
(ניתן ללחוץ על התמונה ולהגדיל אותה)
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית המטרה.
- יש למקם את 3 הנקודות \(A, B, C\) כך שתתקבל תיבה המסורטטת בפרספקטיבה.
- לחצו על כפתור "בדיקה":
אם כל שלוש הנקודות במקום מתאים, צבען ישתנה לירוק, ופאות התיבה יופיעו.
אם הנקודות (כולן או חלקן) במקום שאינו מתאים, צבען ישתנה לאדום. - ניתן להשוות את מיקום הנקודות עם התיבה המוצגת בחלקו הימני של היישומון.
- ניתן להיעזר ב-3 הישרים המנחים: ישר אופקי, ישר אנכי, וישר משופע.
ניתן להזיז ישר: יש למקם את העכבר על סימן ה"+" ולגרור את העכבר אל מיקום הישר הרצוי.
את הישר המשופע ניתן לסובב: יש למקם את העכבר על סימן ה"x", ולגרור את העכבר בזווית השיפוע המבוקשת.
פתרון מדרגה 3
במדרגה זו התלמידים בונים תיבה בהסתמך על התיבה הנתונה שמסורטטת לפי העקרונות של הפרספקטיבה.
(ניתן ללחוץ כל תמונה ולהגדיל אותה)
יהיו תלמידים אשר "יעתיקו" את התיבה הנתונה – כלומר יגדירו את הממד השלישי של התיבה שווה לזה שבתיבה המופיעה בתמונה מימין.
תלמידים אחרים עשויים לבנות תיבה אחרת.
לשיקול דעת של המורה אם להתייחס לאפשרויות שונות של תיבות שאפשר לבנות בהינתן פאה קדמית בלבד.
הערה לשיקול דעת של המורה:
האם לערוך בשלב זה דיון לגבי יחידות התיבה (אפשר לערוך את הדיון לאחר בעיית המטרה או בבעיית סיכום, או בכלל לא לדון בכך – הדבר תלוי ברמת הכיתה ובשיקולים דידקטיים של המורה).
הרי בחירת מיקום הנקודה הראשונה שמגדיר את עומק התיבה (למשל נקודה A כפי שמוצג בתמונות בטבלה למעלה) הינה שרירותית.
התנאי היחיד, שהנקודה צריכה להיות על הקו המחבר אחד הקודקודים של הפאה הקדמית של התיבה, עם נקודת המגוז.
לכן, קיימות אינסוף תיבות שהמלבן הנתון מהווה את הפאה הקדמית שלהן.
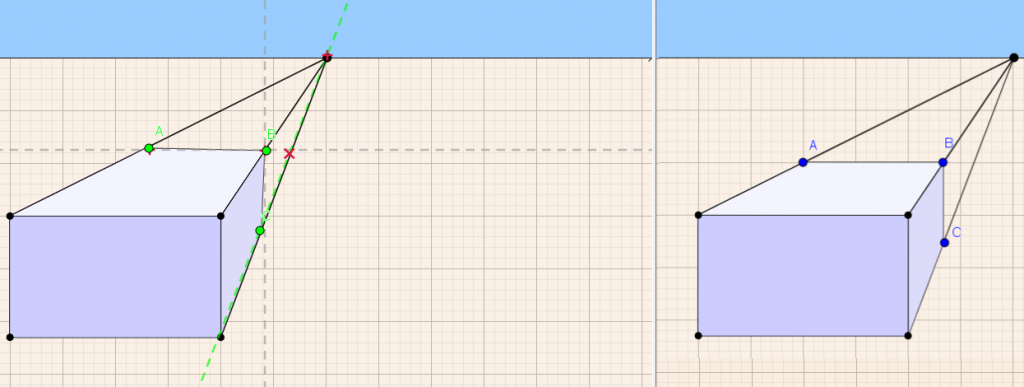
מטרות מדרגה 3
- אבני הבניה: מלבן המייצג פאה קדמית של תיבה ושני קווים מקבילים, לסרטוט של הפאה העליונה של התיבה. זאת בהינתן תיבה שלמה המסורטטת לפי העקרונות של פרספקטיבה.
התנאי הוא שבשתי התיבות, מלבנים שמייצגים את הפאה הקדמית, הינם חופפים.
- אילו מרכיבי התיבה המקורית (קודקודים, מקצועות, פאות) גלויים לעין?
\(\space\) - דמיינו לכם הזזה אופקית של תיבה זו (ימינה/שמאלה).
מה נשאר קבוע ומה משתנה בהזזה כזו של התיבה?
\(\space\) - דמיינו לכם הזזה אנכית של תיבה זו (מעלה/מטה).
מה נשאר קבוע ומה משתנה בהזזה כזו של התיבה?
\(\space\) - האם ייתכן מצב שבהזזות שונות של התיבה המקורית מתקבלת תיבה שבה ניתן לראות (תוכלו להיעזר בתמונות שלפניכם ו/או ביישומון):
\(\space\)
• ארבע פאות של תיבה
• שלוש פאות של תיבה
• שתי פאות של תיבה
• רק פאה קדמית של תיבה
\(\space\)
בכל מצב אפשרי: תארו את סוגי ההזזות (אופקית / אנכית) ומיקום התיבה ביחס לקו האופק ונקודת המגוז.
התייחסו למצבים שונים (אם יש כאלה).
השוו את התשובות שלכם עם תשובותיהם של חברים שלכם.
1
2
3
4
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
- אילו שאלות נוספות עולות לכם לגבי התיבות המתקבלות בהזזות שונות של התיבה המקורית?
- היעזרו בסרגלי הגרירה והזיזו את התיבה אופקית ואנכית.
- לאחר שינוי סרגלי הגרירה ממצב האיתחול בו הם נמצאים, תופיע התיבה "קודקודים".
ואז ניתן יהיה להציג את הקודקודים של התיבה המקורית, והתיבה המוזזת.
פתרון בעיית הסיכום
התלמידים יסיקו כי למרות שהזזות של תיבה מקורית יוצרות אשליה של שינוי מידות התיבה, למעשה מדובר באותה התיבה הבנויה לפי עקרונות הפרספקטיבה.
הצופה נמצא באותו המקום – הרי מיקום של נקודת המגוז אינו משתנה (שינוי מיקום הצופה גורם לשינוי מקום של נקודת המגוז). בהזזות של התיבה, השינוי חל רק בזווית שבה הצופה רואה את הפאה הקדמית של התיבה.
התלמידים יכולים להסיק שבהזזות שונות של התיבה, לכל היותר ניתן לראות שלוש מפאות התיבה. כך, בתיבה המקורית ניתן לראות את הפאה הקדמית, הפאה העליונה והפאה הימנית.
התלמידים יכולים לבצע תחילה רק אחת ההזזות של התיבה (אופקית / אנכית) ולהסיק לגבי מצבים אפשריים.
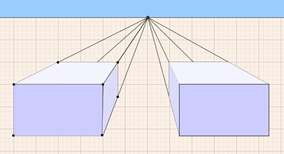
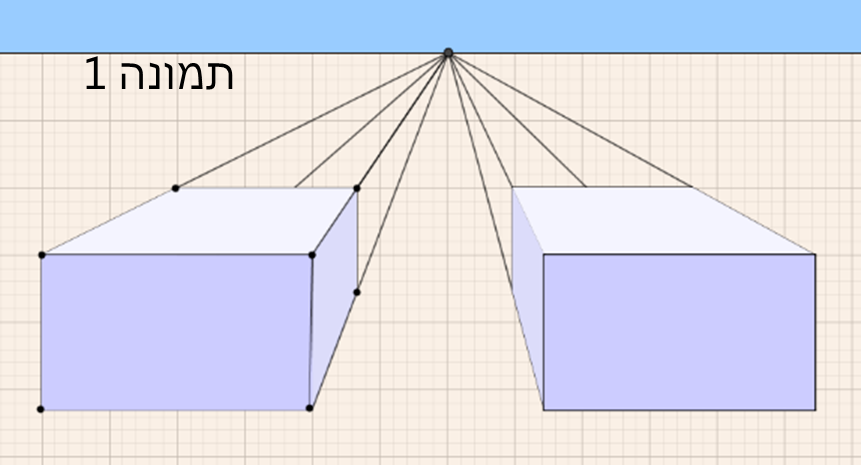
כך למשל, בתמונה 1, בתיבה שמתקבלת בהזזה אופקית של התיבה המקורית, ניתן לראות 3 פאות (רק שהפעם רואים את הפאה השמאלית).
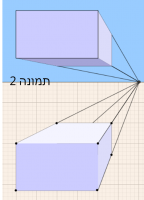
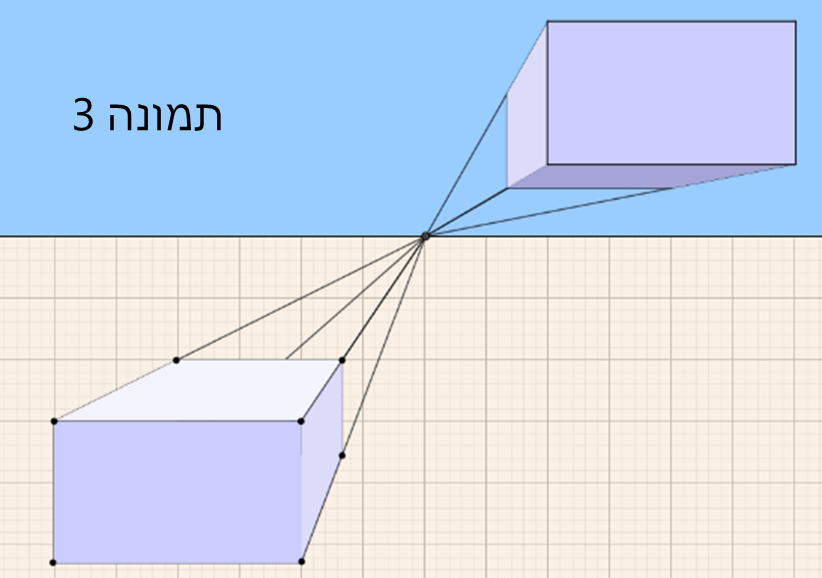
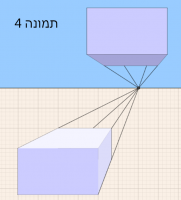
בהזזות של התיבה המקורית מעל קו האופק מתקבלים מצבים בהם ניתן לראות 3 פאות (תמונות 2 ו-3) או 2 פאות (התחתונה והקדמית – תמונה 4).
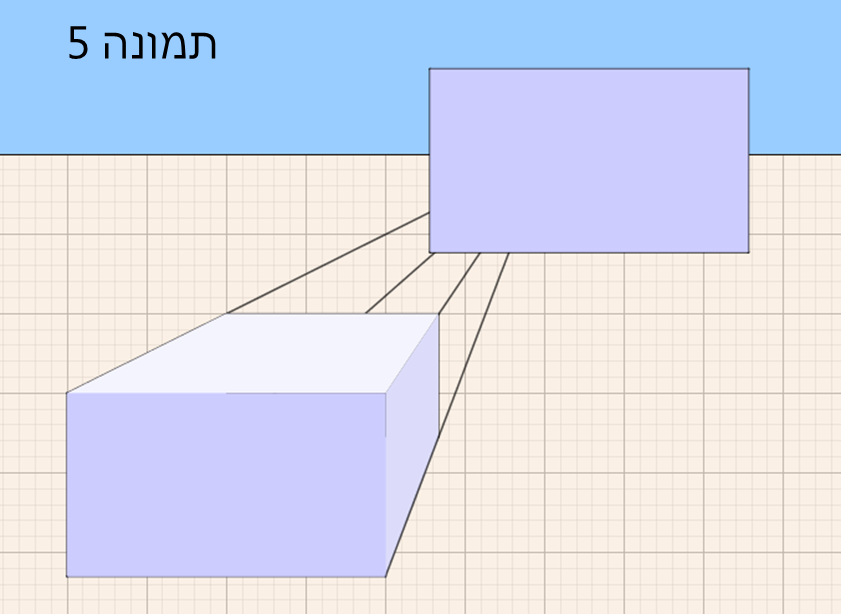
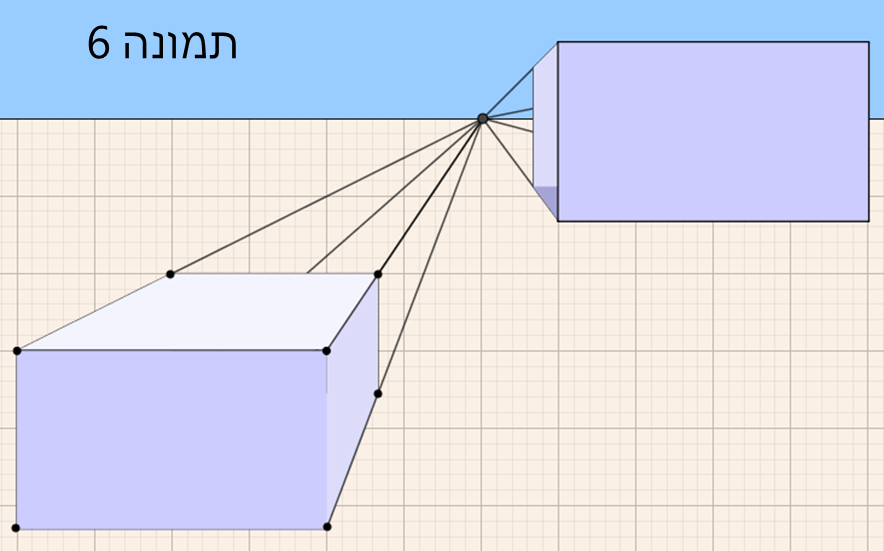
כאשר הפאה הקדמית של התיבה נמצאת ברמה של קו האופק, ניתן להבחין בין המצבים בהם ניתן לראות רק את הפאה הקדמית של התיבה (כשנקודת המגוז בתוך הפאה הקדמית – תמונה 5) והמצבים בהם ניתן לראות שתיים מפאות התיבה (למשל, הפאה הקדמית והפאה השמאלית, כמו תמונה 6).
1
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
2
3
4
5
6
