אשכול פרספקטיבה – חלק ג – עמודי תאורה במרחקים שווים – למורה
הנחיות למורה
אשכול מס' 3 מתוך 5 אשכולות.
יחידה:
אמנות
כיתה מומלצת:
כיתה ט, כיתה י
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (קונטקסט):
- שימוש בעקרונות של פרספקטיבה חד-מגוזית בציור.
ידע ומיומנויות מתמטיים נדרשים
| נושא | מושגים | מיומנויות |
|---|---|---|
| מצבים הדדיים בין ישרים: ניצבות והקבלה | – ישרים מקבילים – ישרים מאונכים | – זיהוי וסרטוט של ישרים מקבילים וישרים מאונכים. |
| טרפז | – זיהוי טרפזים ושימוש בהגדרה. | |
| דמיון משולשים | – זיהוי של משולשים דומים בהסתמך על משפט דמיון ז.ז. – הסקת מסקנות מהדמיון. |
|
| משפט תאלס |
מטרות האשכול
- להכיר את עקרונות הפרספקטיבה החד-מגוזית בציור של אובייקטים בעלי גובה זהה, הנמצאים במרחקים
שווים זה מזה. - להשתמש במושגים גיאומטריים כדי להוכיח את תקפות הבנייה כפי שבאה לידי ביטוי בציור.
ידע ומיומנויות מתמטיים נלמדים (חדשים)
(רשות) ממוצע הרמוני של שני גדלים.
שלב הלמידה המומלץ
- אפשרי בכיתה ט, לאחר למידת הנושא "טרפז"
- ו/או בכיתה י, לאחר שלמדו דמיון משולשים.
תפקיד המדרגות
מדרגה 1 – התמקדות בהוכחה בהינתן סרטוט גיאומטרי.
מדרגה 2 – חזרה קצרה על עקרונות הפרספקטיבה החד-מגוזית.
מדרגה 3 – פתרון בהינתן סרטוט גיאומטרי והוכחה חלקית.
ארגון כיתה מומלץ
- למידה בזוגות או בקבוצות.
- מומלץ לפתוח את השיעור בהיכרות/ חזרה על מושגים עיקריים של פרספקטיבה חד-מגוזית.
לשיקול דעת של המורה אם להתחיל מבעיית ההקדמה או ישר לגשת לפתרון של בעיית המטרה. לפני בעיית המטרה כדאי שתלמידים יכירו את השיקולים הגיאומטריים שמאחורי הציור, המוצגים ב"תיאור סיטואציה". - במידה והתלמידים נחשפים לבעיית ההקדמה, כדאי לדון בדרכים שונות לפתרון ולהנמקות לתקפות או אי-התקפות של הבנייה המוצעת על ידי התלמידים.
- המורה יאפשר לתלמידים לענות על השאלות באשכול באופן עצמאי, כשהם יכולים להיעזר במדרגות וביישומונים.
המורה יעודד תלמידים שמתקשים להיעזר במדרגות, לשתף פעולה, ולהדריך את התלמידים במקרה שישנן אי הבנות. - המורה יערוך דיון כיתתי, סביב השאלות שעלו במהלך הפתרון של השאלות באשכול.
לפי שיקול דעת של המורה אם כדאי לערוך דיוני ביניים במידה ומזהה קושי.
שאלות מומלצות לדיון כיתתי
- תארו דרכים גיאומטריות שונות לציור של עמוד התאורה השלישי בשורה, כאשר הצייר עומד מול העמוד השמאלי ונמקו.
- אילו מהדרכים שהצעתם, מאפשרות לצייר את העמוד שלישי לפי עקרונות הפרספקטיבה חד-מגוזית כאשר הצייר נמצא במקום אחר? בססו את קביעתכם על שיקולים גיאומטריים, שמבוססים על הגדרות ומשפטים שלמדתם.
אשכול פרספקטיבה – חלק ג – עמודים במרחקים שווים
תיאור סיטואציה
פרספקטיבה בציור
אנחנו חיים בעולם תלת-ממדי, אך כאשר רוצים לתאר אותו בציור או בצילום אנחנו עושים את זה בדפים דו-ממדיים. הדרך לייצג אובייקטים תלת ממדיים על משטח דו-ממדי, כמו בציור או בסרטוטים אדריכליים, נקראת פרספקטיבה.
באשכול זה תכירו כיצד המתמטיקה שלמדתם בבית הספר עוזרת להבין את יחסי הגומלין בין המרכיבים השונים של האובייקטים (אורכים, מקבילות, מאונכות וכו'). היעזרו בגיאומטריה של המישור כדי להוכיח יחסים בין אובייקטים.
כדי לתאר מצב תלת-ממדי בדפים דו-ממדיים משתמשים בשיטה המבוססת על העובדה שכל עצם נראה קטן יותר, ככל שהוא רחוק יותר מהעין. השיטה נקראת פרספקטיבה (בעברית תִּשְקוֹפֶת). המושג שאוב מהמילה הלטינית perspicere שמשמעה "לראות מבעד", לראות דרך חלון שקוף.
הגדרות
- לכל ציור או צילום יש קו ראיה יחיד שהוא בגובה העיניים של הצייר או הצלם.
קו זה נקרא קו האופק. קו האופק מקביל למסגרת התמונה. - נקודת המָגוֹז או נקודת ההיעלמות היא הנקודה על קו האופק שבה הדברים "נעלמים".
- כל הקווים המקבילים ביניהם שכיוונם לקו האופק מתכנסים בנקודת המגוז. קווים אחרים שמקבילים זה לזה יישארו מקבילים גם בפרספקטיבה. כך נוצרת אשליה של עומק.
- עצמים שווים בגודלם במציאות (כמו מבנים, עצים, הרים, אנשים וכו'), ייראו בציור ובצילום קטנים יותר ככל שהם רחוקים יותר. באשכול זה נעסוק בפרספקטיבה חד מָגוֹזית – פרספקטיבה שיש בה נקודת מגוז אחת.
הידעתם? משתמשים בפרספקטיבה בהרבה תחומים: באומנות- ציורים, באדריכלות, בתכנון מבנים, עיצוב פנים וכיום גם בגרפיקה ממוחשבת.
1. בעיית הקדמה
לפניכם שני עמודי תאורה (ראו תרשים 2). הצייר ואתם עומדים מול העמוד השמאלי.
- תכננו את המיקום של העמוד השלישי בשורה, כך שהעמודים יהיו ממוקמים במרחקים שווים.
\(\space\) - סרטטו בתרשים 1 את העמוד השלישי ללא כלי מדידה (הציעו דרכים שונות).
\(\space\) - הוכיחו מדוע שלושת עמודי התאורה בסרטוט שלכם נמצאים במרחקים שווים.
תרשים 1
תרשים 2
- אחרי שפתרתם את השאלות בבעיית ההקדמה, המשיכו לבעיית המטרה.
- גררו ומקמו את הנקודות H (במיקום המתאים לתחתית העמוד) ואת G (במיקום המתאים לחלק העליון של העמוד) במקום המתאים, ולחצו על בדיקה.
תוכלו להיעזר בכלי גאוגברה השונים המופיעים בצד שמאל (רקע תכלת). - אם צדקתם, יופיע, בחלון התחתון של היישומון, העמוד השלישי.
כמו כן, יופיעו 2 כפתורים של מבט מלמעלה ומבט מקדימה, שיאפשרו לשנות את התצוגה בחלון התחתון. - אם טעיתם, תופיע הודעת שגיאה. נסו שוב.
- ניתן להציג או להסתיר את התמונה.
פתרון לבעיית ההקדמה
הצעות לפתרונות אפשריים באמצעות היישומון:
אפשרות 1
- לסרטט קווים מקבילים FC||DE (ניתן להשתמש בכלי של קו אופקי
).
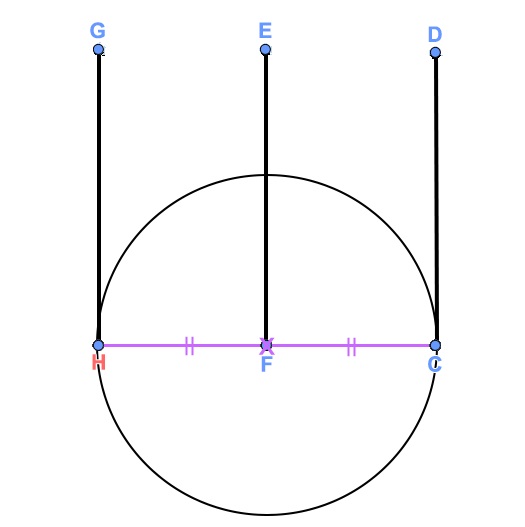
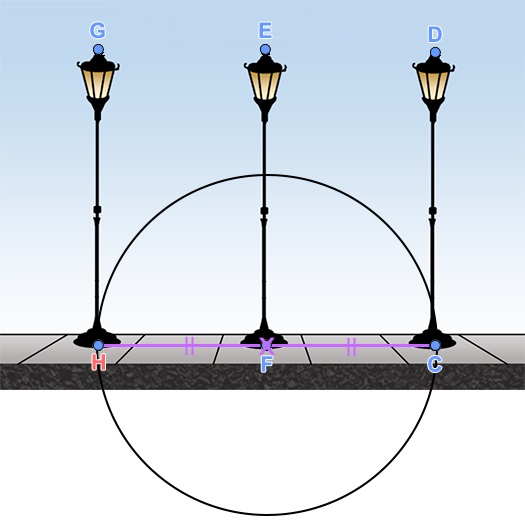
קצוות העמוד HG יהיו על הישרים האלה. - לסרטט מעגל באמצעות מרכז (F) ונקודה על המעגל (C). בנייה כזו מאפשרת באופן מיידי, למצוא את המיקום
של הנקודה H על הישר FC. נקודה זו מסמנת את מיקום העמוד השלישי בשורה.
FC=FH – רדיוסים במעגל. - לסרטט דרך הנקודה H ישר מאונך ל-CF (ניתן להשתמש בכלי של קו אנכי
).
הנקודה G הינה נקודת החיתוך של הקו האנכי שסורטט ושל הישר DE. - התקבל קטע GH שמייצג את העמוד השלישי ומקיים:
\(GH⊥FC\) , \(FH=FC\) ו- \( CD=EF=GH\)
אפשרות 2
- לסרטט קווים מקבילים FC||DE (ניתן להשתמש בכלי ).
- לסמן נקודה M כאמצע הקטע CD ולסרטט MK||DE (ניתן להשתמש בכלי
).
הנקודה K היא אמצע הקטע EF. התלמידים צריכים להוכיח טענה זו. למשל,- התלמידים עשויים להסתמך על כך ש- MK||DE ולכן כל הנקודות על הישר DE נמצאות באותו מרחק מהישר MK. ולכן EK=DM.
- תלמידים אחרים עשויים לזהות כי המרובע KEDM הוא מלבן ולהסתמך על תכונה של מלבן:
במלבן צלעות נגדיות שוות. נתון כי EF=CD (עמודי התאורה בגובה זהה).
- לסרטט קו ישר DK. קו זה יחתוך את CF בנקודה H. נקודה זו מסמנת את מיקום העמוד השלישי בשורה.
כעת נשאר להוכיח כי HF=FC.
למשל, באמצעות חפיפת משולשים DEK ו-HFK או באמצעות קטע אמצעים במשולש DHC, או באמצעות שטחים.
מטרות בעיית ההקדמה
הבעיות באשכול זה מתייחסות לציור של עמודי תאורה שנמצאים במרחקים שווים (כל העמודים בעלי גובה זהה).
בעיית ההקדמה מציגה ציור חלקי של שני עמודי תאורה ועל הצייר לצייר את העמוד השלישי משמאל.
בבעיה רשום כי בעת היצירה הצייר עומד מול העמוד השמאלי. הבעיה מזמנת את התלמידים להציע דרכים שונות לבניית העמוד השלישי תוך שימוש ביישומון, בו יש מאגר כלים לבנייה. על התלמידים לבנות ולהוכיח כי הבנייה שהציעו הינה תקפה.
שימו לב, ייתכן והתלמידים יעשו הכללות יתר בהסתמך על אובייקטים המופיעים בציור. למשל, תלמידים אחדים עשויים לחשוב כי הנקודות המסומנות על עמודי התאורה הן נקודות אמצע (וזה לא נכון). זאת הזדמנות לדון עם התלמידים על כך שלא ניתן להסתמך על העין, אלא רק על הנתונים המוצגים במשימה.
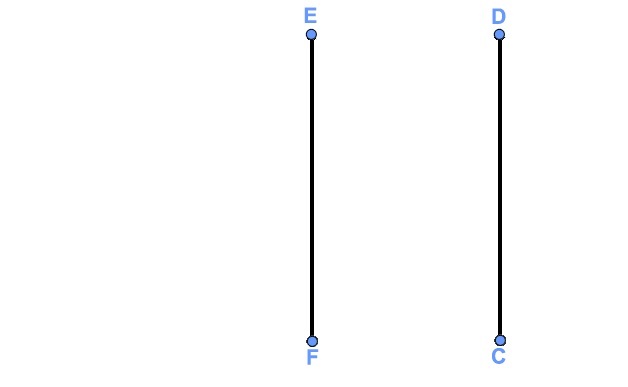
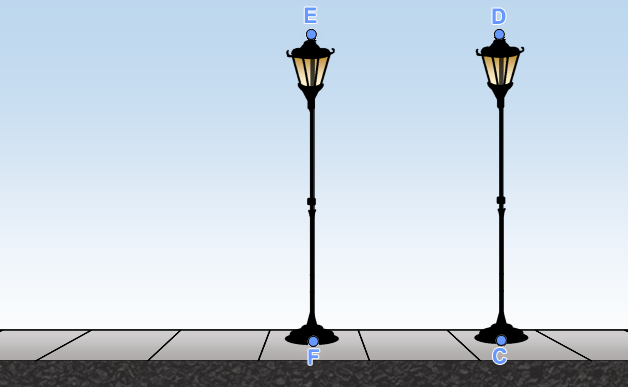
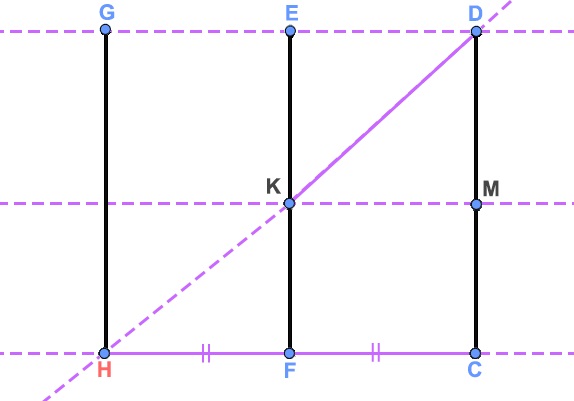
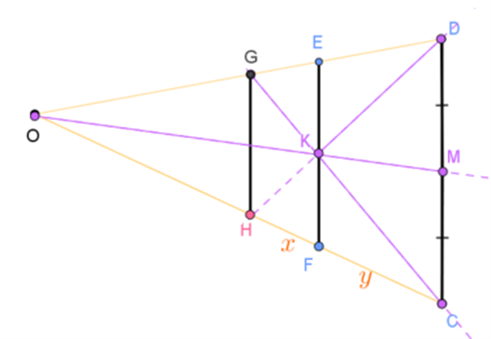
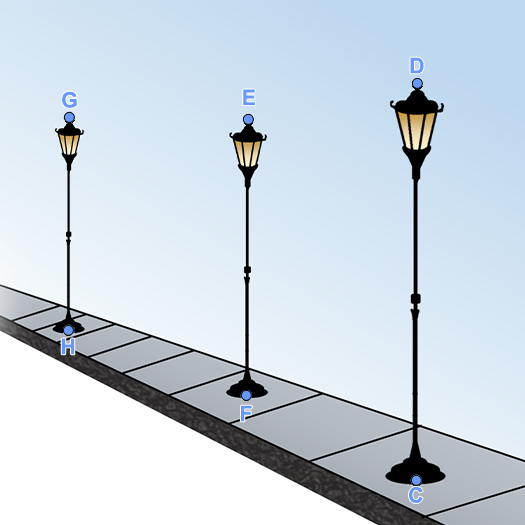
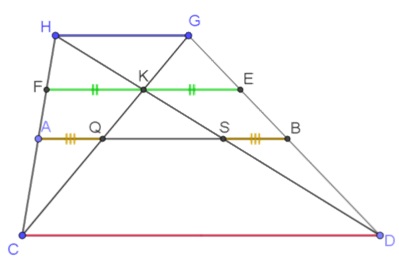
לפניכם ציור של 3 עמודי תאורה בפרספקטיבה חד-מגוזית.
במציאות, העמודים האלה בעלי גובה זהה והם נמצאים במרחקים שווים זה מזה.
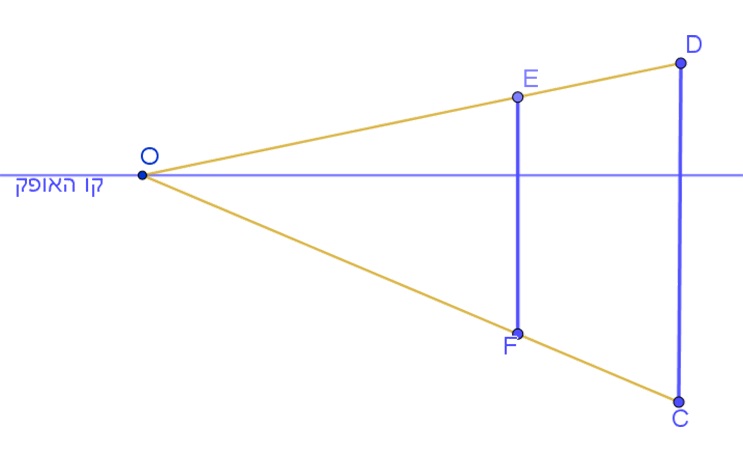
צייר מצייר את הציור לפי חוקי הפרספקטיבה באופן הבא:
- בוחר את קו האופק ואת נקודת המגוז O.
- מצייר את קטע DC, המתאר את עמוד התאורה הראשון.
- מחבר את קצות קטע DC עם נקודת המגוז.
- מצייר את קטע EF, המתאר את עמוד התאורה השני, כך שהנקודה E על OD והנקודה F על OC ומתקיים כי EF||DC.
(ראו תרשים 1).
תרשים 1
5. את העמוד השלישי הצייר מצייר כך:
- מסמן את M, אמצע DC, ומחבר את הנקודה M עם נקודת המגוז O.
- MO חותך את קטע EF בנקודה K.
- המשך הישר DK, חותך את OC בנקודה H.
- דרך הנקודה H, מסרטט את ישר HG, המקביל ל-EF.
- הקטע HG מתאר את העמוד השלישי.
(ראו תרשים 2).
תרשים 2
6. באופן דומה מסרטטים את עמודי התאורה הבאים בשורה.
2. בעיית מטרה
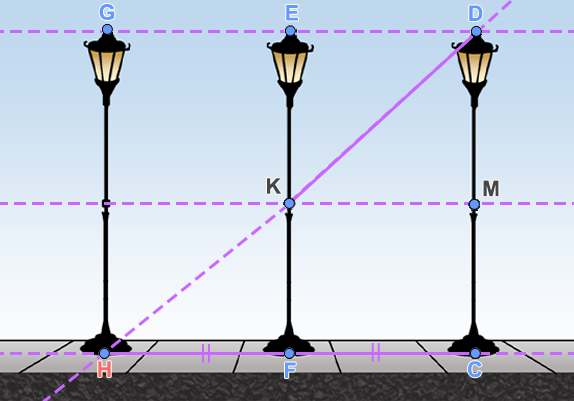
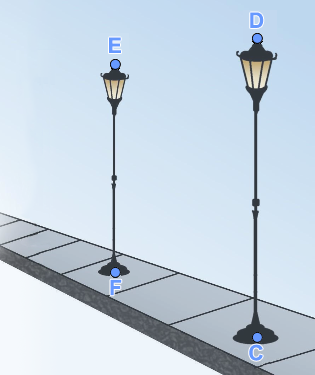
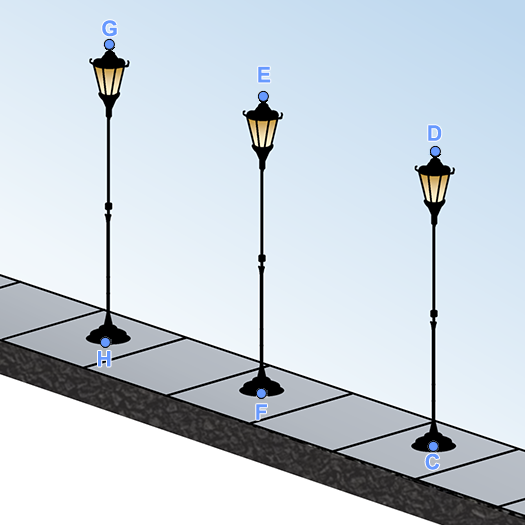
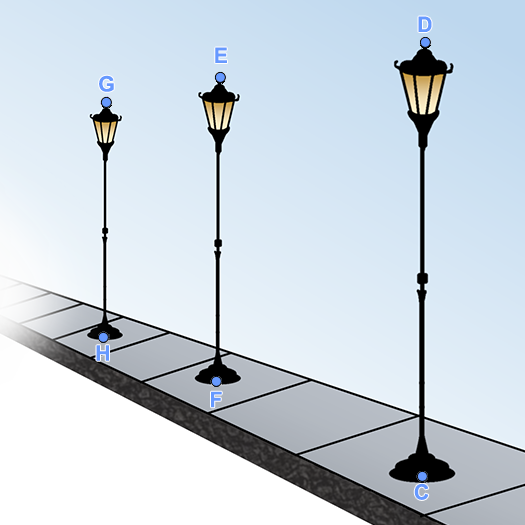
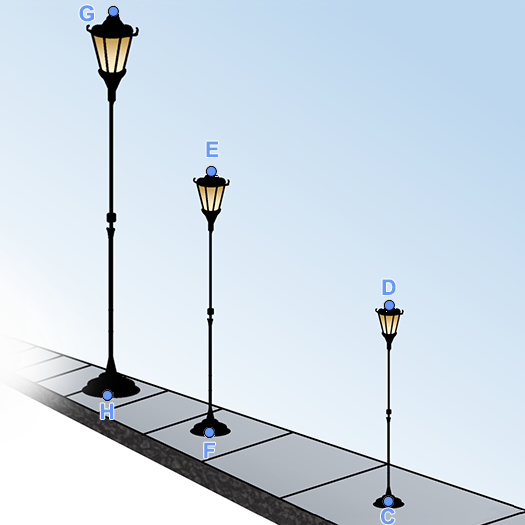
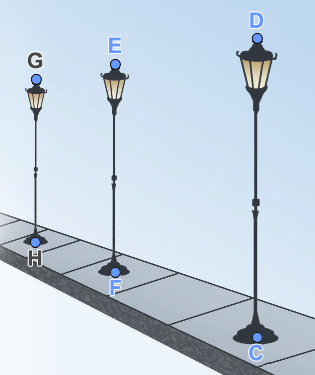
לפניכם שני ציורים של עמודי תאורה.
במציאות, העמודים האלה בעלי גובה זהה והם נמצאים במרחקים שווים זה מזה.
האומן הסביר כי התבסס בציור על אותם השיקולים הגיאומטריים, כפי שתוארו ב"תיאור הסיטואציה" שבאשכול זה.
- לגבי כל ציור, זהו את המקום משוער של האומן בעת היצירה.
\(\space\) - הוכיחו מדוע ה"בנייה" בשני הציורים תואמת את המציאות.
ציור 1
ציור 2
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
- במידת הצורך, פתרו את השאלות במדרגה 1.
- בחלון העליון של היישומון:
גררו ומקמו את הנקודות H (במיקום המתאים לתחתית העמוד) ואת G (במיקום המתאים לחלק העליון של העמוד) במקום המתאים, ולחצו על בדיקה.
תוכלו להיעזר בכלי גאוגברה השונים המופיעים בצד שמאל (רקע תכלת). - אם צדקתם, יופיע, בחלון התחתון של היישומון, העמוד השלישי.
כמו כן, יופיעו 2 כפתורים של מבט מלמעלה ומבט מקדימה, שיאפשרו לשנות את התצוגה בחלון התחתון. - אם טעיתם, תופיע הודעת שגיאה. נסו שוב.
- ניתן להציג או להסתיר את התמונה.
- בחלון העליון של היישומון:
גררו ומקמו את הנקודות H (במיקום המתאים לתחתית העמוד) ואת G (במיקום המתאים לחלק העליון של העמוד) במקום המתאים, ולחצו על בדיקה.
תוכלו להיעזר בכלי גאוגברה השונים המופיעים בצד שמאל (רקע תכלת). - אם צדקתם, יופיע, בחלון התחתון של היישומון, העמוד השלישי.
כמו כן, יופיעו 2 כפתורים של מבט מלמעלה ומבט מקדימה, שיאפשרו לשנות את התצוגה בחלון התחתון. - אם טעיתם, תופיע הודעת שגיאה. נסו שוב.
- ניתן להציג או להסתיר את התמונה.
פתרון לבעיית המטרה
שלבי ההוכחה
- \(\space\space\)K אמצע הקטע EF
\(\space\) - \(\space\space\)\(\large\frac{EF}{GH}\normalsize=\large\frac{2y}{(x+y}\)
\(\space\) - \(\space\space\)\(\large\frac{EF}{GH}\normalsize=1 \Longleftrightarrow x=y\)
כלומר, הבנייה תואמת את המציאות.
הוכחה אפשרית
- \(\space\space\)לפי הבנייה מתקיים כי \(CD||FE\) \(\Leftarrow\space\space\)
(1.1) \(\triangle{OEK}\sim\triangle{ODM}\) (לפי משפט דמיון ז.ז) ולכן \(\large\frac{OK}{OM}\normalsize=\large\frac{EK}{DM}\)
(1.2) \(\triangle{OKF}\sim\triangle{OMC}\) (לפי משפט דמיון ז.ז) ולכן \(\large\frac{OK}{OM}\normalsize=\large\frac{KF}{CM}\)
(1.3) מ- (1.1) , (1.2) ומהנתון שהקטע OM הוא תיכון, נובע כי \(FK=KE\).
- \(\space\space\)מהנתון \(FE||HG\) נובע כי: \(\triangle{CFK}\sim\triangle{CHG}\) (לפי משפט דמיון ז.ז)
\(\space\)
\(\Leftarrow\space\space\space\space\) \(\large\frac{FK}{HG}\normalsize=\large\frac{CF}{CH}\normalsize=\large\frac{y}{x+y}\)
\(\space\)
כיוון ש- \(FK=KE\), לכן מתקיים כי \(\large\frac{EF}{GH}\normalsize=\large\frac{2y}{x+y}\).
(ניתן ללחוץ על התמונה ולהגדיל אותה)
מטרות בעיית המטרה
לאחר בעיית ההקדמה, התלמידים נפגשים עם ציור של אותם עמודי התאורה – רק שהפעם הצייר לא נמצא מול העמוד השמאלי, אלא זז הצידה (ימינה מהעמוד הראשון המסומן ב- CD). עליו לצייר את העמוד השלישי בהסתמך על הכללים של פרספקטיבה חד-מגוזית. ב"תיאור סיטואציה" מוצג אופן הציור – מומלץ לדון עם התלמידים על אופן הבנייה המוצג, לפני שניגשים לפתרון של בעיית המטרה. אם אופן בנייה זה (אפשרות 2) לא עלה בפתרון של בעיית ההקדמה, דיון סביב בנייה זו יערך בבעיית המטרה.
בבעיית המטרה על התלמידים לזהות את מיקום הצייר בעת היצירה של כל אחד מהציורים ולבנות את העמוד השלישי בהסתמך על ההסבר המוצג בתיאור הסיטואציה. השאלה המאתגרת היא להוכיח כי הבנייה בשני הציורים תואמת את המציאות. (הוכחה אפשרית לגבי ציור front מוצגת למעלה).
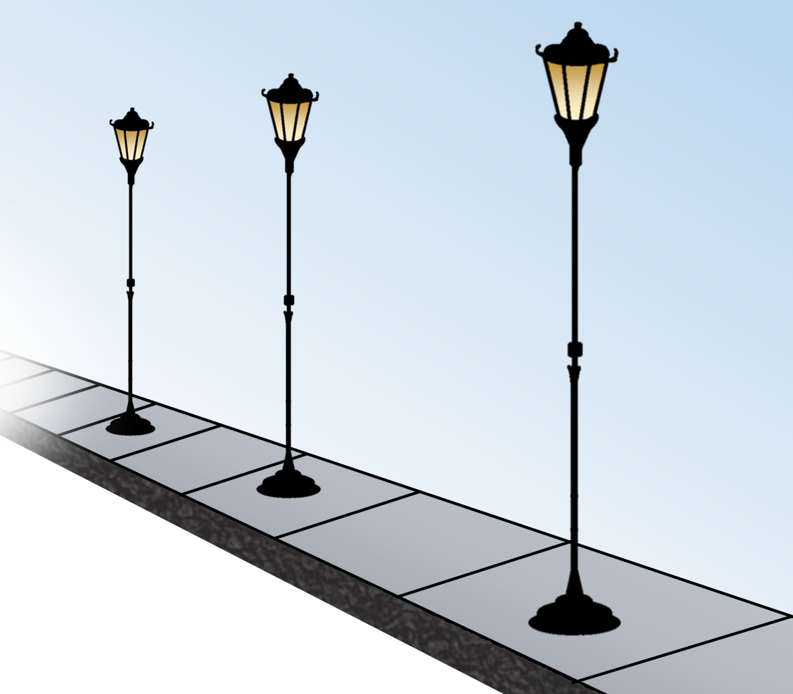
2.1. מדרגה 1 לבעיית המטרה
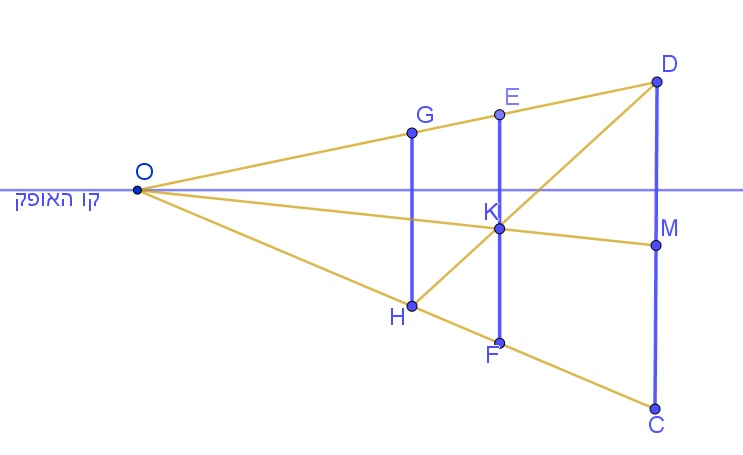
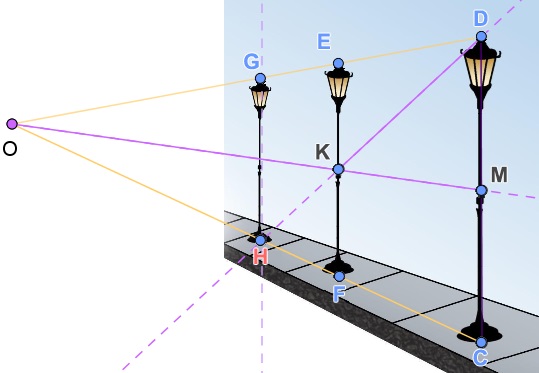
לפניכם שני ציורים של עמודי תאורה, בצירוף קווי העזר של האומן.
במציאות, העמודים האלה בעלי גובה זהה והם נמצאים במרחקים שווים זה מזה.
האומן הסביר כי התבסס בציור על אותם השיקולים הגיאומטריים, כפי שתוארו ב"תיאור הסיטואציה" שבאשכול זה.
הוכיחו מדוע ה"בנייה" בשני הציורים תואמת את המציאות.
ציור 1
ציור 2
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית המטרה.
- במידת הצורך, פתרו את השאלות במדרגה 2.
- בחלון העליון של היישומון:
גררו ומקמו את הנקודות H (במיקום המתאים לתחתית העמוד) ואת G (במיקום המתאים לחלק העליון של העמוד) במקום המתאים, ולחצו על בדיקה.
תוכלו להיעזר בכלי גאוגברה השונים המופיעים בצד שמאל (רקע תכלת). - אם צדקתם, יופיע, בחלון התחתון של היישומון, העמוד השלישי.
כמו כן, יופיעו 2 כפתורים של מבט מלמעלה ומבט מקדימה, שיאפשרו לשנות את התצוגה בחלון התחתון. - אם טעיתם, תופיע הודעת שגיאה. נסו שוב.
- ניתן להציג או להסתיר את התמונה.
- בחלון העליון של היישומון:
גררו ומקמו את הנקודות H (במיקום המתאים לתחתית העמוד) ואת G (במיקום המתאים לחלק העליון של העמוד) במקום המתאים, ולחצו על בדיקה.
תוכלו להיעזר בכלי גאוגברה השונים המופיעים בצד שמאל (רקע תכלת). - אם צדקתם, יופיע, בחלון התחתון של היישומון, העמוד השלישי.
כמו כן, יופיעו 2 כפתורים של מבט מלמעלה ומבט מקדימה, שיאפשרו לשנות את התצוגה בחלון התחתון. - אם טעיתם, תופיע הודעת שגיאה. נסו שוב.
- ניתן להציג או להסתיר את התמונה.
מטרות מדרגה 1
- במדרגה זו על התלמידים לתרגם את הסיטואציה למצב גיאומטרי הנתון (ללא צורך בבניה) ולהתמקד בהוכחה בלבד.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית המטרה.
- במידת הצורך, פתרו את השאלות במדרגה 3.
תרשים 1
נתון: \(CD=FE=HG\) , \(CF=HF\)
תרשים 2
נתון: \(CD>FE>HG\) , \(CF<HF\)
תרשים 3
נתון: \(CD>FE>HG\) , \(CF>HF\)
תרשים 4
נתון: \(CD<FE<HG\) , \(CF>HF\)
(ניתן ללחוץ על כל תמונה ולהגדיל אותה)
מטרות מדרגה 2
- הבעיה המוצגת במדרגה זו מחזירה את התלמידים לעקרונות של פרספקטיבה חד-מגוזית בנוגע ליחסי הגדלים של האובייקטים והמרחקים ביניהם.
על התלמידים להיזכר כי עצמים שווים בגודלם במציאות, ייראו בציור קטנים יותר, ככל שהם רחוקים יותר.
2.3. מדרגה 3 לבעיית המטרה
בצד שמאל מופיעים הסברי האומן לציור.
- מהו סוג המרובע CDEF שנוצר בין שני עמודי התאורה הראשונים, כאשר האומן מצייר אותם בפרספקטיבה חד-מגוזית?
נמקו.
\(\space\) - האומן צייר את העמוד השלישי בהתבסס על שיקולים גיאומטריים וטען שהציור שלו מתאים למציאות.
לפניכם כמה שיקולים גיאומטריים שהפעיל.
הסבירו את השקולים והשלימו את ההוכחה.
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית המטרה.
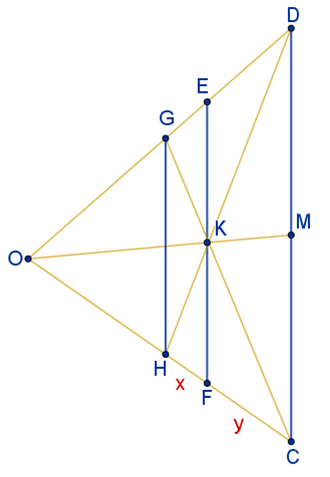
בסרטוט: \(\large\frac{HF}{FC}\normalsize=\large\frac{x}{y}\)
במציאות: \(HF=FC\) \(\Longleftrightarrow\) \(x=y\)
רציתי לצייר את העמוד השלישי במקום כזה, כך שיתקיים:
אם: \(x=y\)
אז: \(CD=EF=GH\)
גיליתי שזה מתקיים כאשר העמוד השני (כלומר EF) ממוקם בנקודת החיתוך של אלכסוני המרובע HGDC
\(\large\frac{KE}{GH}\normalsize=\large\frac{KF}{GH}\normalsize=\large\frac{x}{x+y}\)
\(\large\frac{EF}{GH}\normalsize=\large\frac{2y}{x+y}\)
אם: \(x=y\)
אז: \(\large\frac{EF}{GH}\normalsize=1\)
\(\Downarrow\space\space\space\space\space\)
\(EF=CD\)
כלומר המרובע CDEF הוא מלבן
וזה תואם את המציאות!
(ניתן ללחוץ על התמונה ולהגדיל אותה)
מטרות מדרגה 3
- במדרגה זו מוצגת הוכחה חלקית של בעיית המטרה ועל התלמידים להבין את הרעיון ולהשלים את ההוכחה.
- לשיקול דעת של המורה האם לחשוף את התלמידים למושג ממוצע הרמוני של שני מספרים ולבטא את אורך הקטע העובר דרך נקודת חיתוך האלכסונים והמקביל לבסיסי הטרפז, באמצעות אורכי הבסיסים: \(FE=\large\frac{2\space\cdot\space HG\space\cdot\space CD}{HG\space+\space CD}\).
\(\space\)
בכך, למעשה, להוכיח את התכונה: הקו המקביל לבסיסי טרפז ועובר דרך נקודת מפגש האלכסונים, הוא ממוצע הרמוני של בסיסי הטרפז.
- לשיקול דעת של המורה, האם להפנות את תשומת ליבם של התלמידים לאובייקט נוסף שנמצא בציור – הקרקע.
דהיינו, כיצד עקרונות הפרספקטיבה החד-מגוזית באים לידי ביטוי בציור האריחים (הבלטות) עליהם עומדים שלושת עמודי התאורה.