אשכול כמה רחוק קו האופק? – למורה
הנחיות למורה
אשכול מס' 1 מתוך 1 אשכולות.
(האשכול עומד בפני עצמו, אין חובה לפתור את האשכולות האחרים)
יחידה:
מדעים
כיתה מומלצת:
כיתה ט, כיתה י
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (קונטקסט):
- מושגים הקשורים לפרספקטיבה לינארית (קו האופק ונקודת מגוז), עקמומיות של כדור הארץ.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| כדור מעגל ועיגול | – מרכז ורדיוס של כדור – מרכז ורדיוס של מעגל | – לזהות מרכז ורדיוס של מעגל בתרשים הנתון. |
| משפט פיתגורס | – רכיבי משולש ישר זווית – שורש ריבועי – משפט פיתגורס | – זיהוי משולש ישר זווית בסרטוט. – שימוש במשפט פיתגורס. – הסקת נתונים חסרים בעזרת משפט פיתגורס. – אוריינות כמותית: חישוב, אומדן ועיגול מספרים לצורך פתרון בעיות. |
| כתיב מדעי | – חזקות | – יכולת לרשום מספרים גדולים בכתיב מדעי. |
| פונקציה | – פונקציה ותכונותיה – קצב השתנות של פונקציה – פונקציה קווית | – קריאת מידע מהגרפים. – מעברים בין ייצוגים שונים של פונקציה. |
מטרות האשכול
- פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך.
- הפתרון מוביל להעמקת ההבנה שמרחקו של צופה לקו האופק מבוסס על הגובה של צופה מהקרקע – העקמומיות של כדור הארץ מאפשרת לנו לראות עצמים רק כאשר הם עולים עד גובה מסוים.
מידע המוצג בטקסט ובתרשים מאפשר להשתמש במודל של משולש ישר זווית, כדי לחשב כמה רחוק יכול לראות הצופה, שנמצא בגובה מסוים מהקרקע. זאת על סמך המשפט הידוע שנלמד בכיתה ח – משפט פיתגורס. - בנוסף, חקירת הייצוג גרפי של הפונקציה (העשרה) המתארת את הקשר בין מרחקו של צופה מקו האופק לבין גובה הצופה מעל פני כדור הארץ, מאפשרת העשרה והעמקה של ידע מתמטי, תוך שימוש בייצוגים שונים של פונקציה.
מערך דידקטי מומלץ
- מומלץ להפעיל את האשכול לאחר שהתלמידים פתרו לפחות את שני האשכולות הראשונים של האשכול פרספקטיבה.
- מומלץ להתחיל את השיעור בהצגת סרטון המוצג בפתיח, בפני כל הכיתה. מומלץ להעלות לדיון קצר את השאלות: האם חשבתם פעם עד כמה רחוק אנחנו יכולים לראות? כיצד תופסת העין של אדם, הנמצא בקטר של הרכבת, את קו האופק? האם וכיצד ניתן למדוד את המרחק לקו האופק?
זאת על מנת לברר מהו הידע הכללי שיש לתלמידים לגבי המושגים הקשורים לנושא כדור הארץ ולהעלות את המוטיבציה והסקרנות שלהם. - אפשר לקרוא יחד עם התלמידים את ההסבר המוצג במדור "תיאור סיטואציה" – הבנת המושגים המרכזיים ושימוש במודל הדו-ממדי המדגים את הסיטואציה.
- בפתרון האשכול נתעלם מהאליפטיות של כדור הארץ ונניח שהוא כדור עגול לחלוטין ברדיוס של 6,371 קילומטר (התייחסות להנחה זו ניתן לראות בתיאור סיטואציה בבעיית מטרה 1).
- בעיית מטרה 1 ניתן להסתפק רק בחישובים מספריים בהסתמך על משפט פיתגורס.
בכיתות ט חזקות ובכיתות י ניתן לבקש מהתלמידים לרשום ביטויים אלגבריים מתאימים.
בבעיית מטרה 2 (העשרה) מוצגת משימת חקר, העוסקת בהסקת מסקנות על פי הייצוג הגרפי של פונקציה ומעודדת מעברים בין הייצוגים שונים (גרפי, מספרי ואלגברי) של הפונקציה.
ארגון כיתה מומלץ
- ארגון הכיתה: למידה בזוגות או בקבוצות.
- ציוד נדרש: מחשבון, מחשב.
- ניהול השיעור: המורה יאפשר לתלמידים לפתור את הבעיות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות.
- המורה יבקש, מתלמידים שסיימו לפתור את הבעיות שבאשכול, להציע שאלה נוספת הקשורה לאשכול ולענות עליה.
- דיון בכיתה:
- התלמידים יציגו ויסבירו את תשובותיהם בדיון. רצוי לאפשר להם להציג דרכים שונות לפתרון.
- יש לאפשר לתלמידים להציג את השאלות הנוספות שחשבו עליהן ולדון בפתרונות שהציעו.
- רצוי שהמורה יבחר, מבין שאלות התלמידים, את השאלות שלדעתו ראוי לדון בהן.
- אפשרות נוספת היא להציע לתלמידים להגיש את השאלות הנוספות ואת פתרונן כעבודת הגשה.
אשכול כמה רחוק קו האופק?
האם חשבתם פעם עד כמה רחוק אנחנו יכולים לראות?
האם וכיצד ניתן למדוד מרחק לקו האופק?
הגיאומטריה שלמדתם בבית הספר, תעזור לכם לענות על השאלה.
אולם כדי שתוכלו להשתמש בידע שלכם בגיאומטריה, נניח כי כדור הארץ הוא "כדור עגול"
בעל רדיוס 6,371 ק"מ (זאת למרות שכדור הארץ אינו כדור מושלם אלא בעל צורה אליפטית).
צפו בסרטון ותארו כיצד תופסת העין של אדם, הנמצא בקטר של הרכבת, את קו האופק.
תיאור סיטואציה
ננסה להציג את הסיטואציה שצפיתם בסרטון באמצעות סרטוט.
אולם תחילה נביא כמה הגדרות ולאחר מכן נתייחס לסרטוט:
- קו האופק הוא קו ראיה אופקי שהוא בגובה העיניים של הצופה.
קו האופק עובר במקום המפגש הדמיוני הנצפה בין השמים לארץ או לים.
\(\space\)
קיומו של קו האופק נובע מעקמומיות פני כדור הארץ, שבעטיה אין הצופה יכול לצפות בפני כדור הארץ מעבר לקו מסוים, הוא קו האופק.
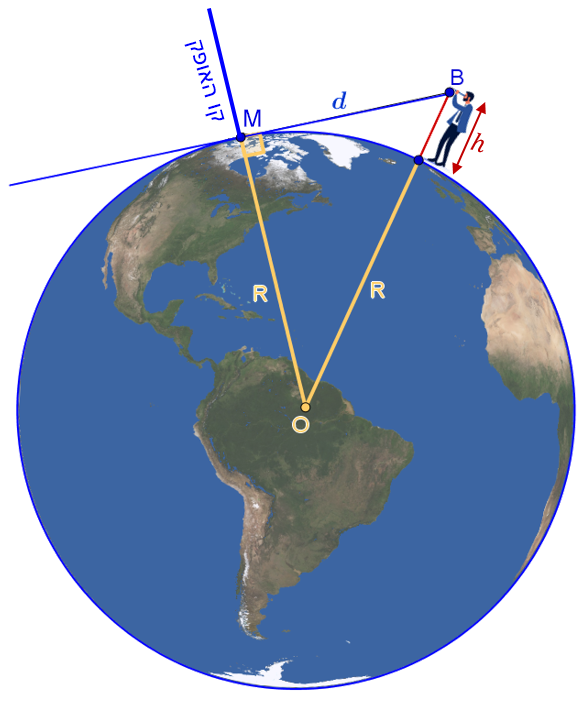
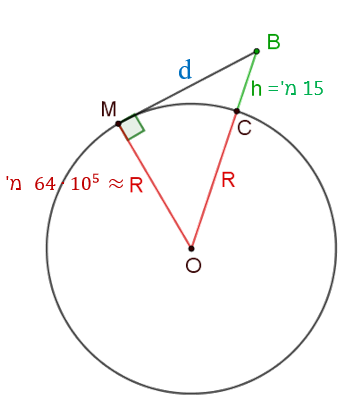
\(\space\) - נסמן בסרטוט (ראו תרשים משמאל):
את רדיוס כדור הארץ ב- R (נניח כי 6,371 ק"מ = R).
ונקודה על קו האופק M – זוהי נקודה שמבט הראיה שלנו מופנה אליה.
\(\space\) - נגדיר את המשתנים ונסמן גם אותם על הסרטוט:
h – גובה עיניו של הצופה מעל פני כדור הארץ.
\(d (BM)\) – המרחק (בקו ישר) אל נקודה על קו האופק.
\(\space\) - נתון כי המשולש OMB שנוצר הוא משולש ישר זווית (\(\measuredangle{M}=90^{\circ}\))
*במציאות כדור הארץ אינו כדור מושלם.
- אחרי שפתרתם את השאלות בבעיית מטרה 1, תוכלו להמשיך לבעיית מטרה 2 – העשרה (רשות).
- במידת הצורך, פתרו את השאלות במדרגה 1.
הצעת פתרון לבעיית מטרה 1 – הקדמה
סעיף א
בפתרון של סעיף א התלמידים יכולים להתבסס על התרשים המופיע ב"תיאור סיטואציה".
התלמידים עשויים לזהות בתרשים כי אדם שעומד באופן אנכי מהווה המשך לרדיוס כדור הארץ,
וקו הראייה d, המכוון אל קו האופק, מאונך לרדיוס המחבר את מרכז הכדור ואת נקודה M על קו האופק (מידע זה מופיע בתיאור סיטואציה).
לכן, משולש OMB – שקודקודיו הם מרכז כדור הארץ (O), נקודה על קו האופק (M) והעין של הצופה (B) – הוא משולש ישר זווית.
במשולש זה, נתונים:
אורך הניצב \(OB=R+h\) (h מרחק עין הצופה מהקרקע, R – רדיוס כדור הארץ)
ואורך היתר R.
לפי משפט פיתגורס:
\(d=\sqrt{(R+h)^2-R^2}=\sqrt{(R+h-R)(R+h+R)}=\sqrt{h(2R+h)}\)
6,371 ק"מ \(R=\) \(\space\space\Leftarrow\space\space\) 6,371,000 מ' \(\space\approx\space\) \(64\cdot10^5\) מ'
מכאן:
מ' 4,382 \(\approx\) \(d \approx \sqrt{1.5\cdot(2\cdot 64\cdot10^5+1.5)}\) \(\space\space\space\)או \(\space\) 4.4 ק"מ \(d \approx\)
* שימו לב: בפתרון בעיית המטרה לא הכרחי לעגל את הרדיוס כפי שמתואר למעלה.
מומלץ לבקש מהתלמידים להתבונן שנית בביטוי \(\sqrt{h(2R+h)}\).
ייתכן ויהיו תלמידים שיזהו כי הגודל h בגורם (2R+h) קטן משמעותי (עד לזניח), ביחס לגודל 2R.
לכן הקירוב \(d≈\sqrt{2R\cdot h}\) הינו קירוב קביל.
כלומר, ניתן לחשב את המרחק גם באופן הבא:
\(d\approx \sqrt{2\cdot 64\cdot 10^5\cdot 1.5}=800\sqrt 30\approx\space 'מ\space4,382\).
משמעות הממצאים שהתקבלו:
4,382 מ' \(d\approx\)
\(\Downarrow\hspace{1cm}\)
צופה הנמצא על שפת הים יכול לראות [את קו האופק] עד למרחק של כ-4.4 קילומטר.
ומה קורה אם הוא נמצא גבוה יותר [נמוך יותר]?
התלמידים יוכלו לענות על השאלה הזאת בהסתמך על הידע הכללי שלהם ואולי גם לבסס את הידע על הביטוי האלגברי \(d\approx\sqrt{2R\cdot h}\).
סעיף ב
בסעיף ב התלמידים יכולים להיעזר בממצאים שלהם מסעיף א,
ולהסתמך על חישוב מרחק הצופה מקו האופק: \(d=\sqrt{h(2R+h)}\), או בקירוב \(d\approx \sqrt{2R\cdot h}\)
ותוך התבססות על התכונה שלמדו לגבי שורש ריבועי \(\sqrt{2R\cdot h}=\sqrt{2R}\cdot\sqrt{h}\)
לחשב את גובה הצופה באופן הבא:
\(d\approx \sqrt{2R\cdot h}\)
\(\Downarrow\hspace{1cm}\)
\(\sqrt{h}\approx\large\frac{d}{\sqrt{2R}}\)
\(\Downarrow\hspace{1cm}\)
380 ק"מ \(h \approx \left( \large\frac{2,200}{\sqrt{2\space\cdot \space 6,371}}\normalsize\right)^2\space\approx\space\)
1.1. מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
כידוע לנו:
R – רדיוס כדור הארץ שווה ל-6,371 ק"מ.
h – גובה עיניו של הצופה מעל פני כדור הארץ.
- בכל סעיף נתון ערכו של h. חשבו בקירוב את ערכי הביטויים הרשומים:
\(\space\)
1. \(\space\)\(\space\)\(\space\)h שווה ל- 3 מטר. למה שווה בקירוב הביטוי \(2R+h\)?
\(\space\)
2. \(\space\)\(\space\)\(\space\)h שווה ל- 1.5 מטר. למה שווה בקירוב הביטוי \(2R+h\)?
\(\space\)
3. \(\space\)\(\space\)\(\space\)h שווה ל- 3 מטר. למה שווה בקירוב הביטוי \(2Rh\)?
\(\space\)
4. \(\space\)\(\space\)\(\space\)h שווה ל- 1.5 מטר. למה שווה בקירוב הביטוי \(2Rh\)?
\(\space\) - אילו מסקנות ניתן להסיק מהסעיפים 1-4 שבסעיף א?
נמקו.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- במידת הצורך, פתרו את השאלות במדרגה 2.
הצעת פתרון למדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
בפתרון הבעיה שמופיעה במדרגה 1, התלמידים עשויים להגיע למסקנה כי הגודל h בגורם (2R+h) שבנוסחה לחישוב המרחק \(d=\sqrt{h(2R+h)}\), קטן משמעותית (עד לזניח) ביחס לגודל 2R.
ולכן הקירוב \(d≈\sqrt{2R\cdot h}\), הינו קירוב קביל.
זאת בהבחנה לביטוי 2Rh שבו הגודל h אינו זניח.
מטרת מדרגה 1 לבעיית מטרה 1
התמודדות עם הקושי העיקרי הצפוי בפתרון של בעיית המטרה, הקשור לרעיון שהקירוב \(d\approx\sqrt{2R\cdot h}\) בנוסחה \(d=\sqrt{h(2R+h)}\), הינו קירוב קביל.
לפניכם סקיצה המתארת את הסיטואציה של מרחק צופה מקו האופק.
המעגל שמרכזו בנקודה O מייצג את כדור הארץ.
הנקודות O, B ו-C נמצאות על קו ישר אחד.
נניח כי:
- רדיוס כדור הארץ הינו 6,371 ק"מ = R.
- גובה העיניים של הצופה מעל פני כדור הארץ הינו 1.5 מ'.
סמנו את הנתונים על הסקיצה וענו:
מהו מרחקו של הצופה ממרכז כדור הארץ (נקודה O)?
\(\space\)
בטאו את התוצאה:
(1) במטרים
(2) בק"מ
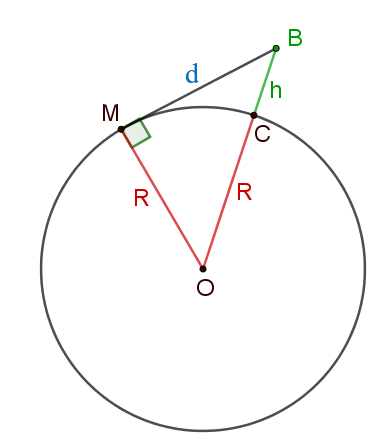
שימו לב: סקיצה משמע סרטוט לא מדויק,
כך למשל, במציאות, רדיוס כדור הארץ (R)
גדול בהרבה יותר מגובה העיניים של הצופה (h).
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
הצעת פתרון למדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
על התלמידים:
- לבטא את המידע לגבי רדיוס כדור הארץ במטרים,
כלומר רדיוס כדור הארץ:
נתון 6,371 ק"מ = R
\(\Downarrow\hspace{1cm}\)
\('מ \space 6,371,000 \space\approx\space 'מ \space 64\cdot 10^5\)
\(\space\) - לסמן את כל הנתונים על התרשים.
\(\space\) - לזהות כי אדם שעומד באופן אנכי מהווה המשך לרדיוס כדור הארץ
ולחשב את מרחקו של הצופה ממרכז כדור הארץ במטרים:
6,371,015 מ' = R + h
\(\space\) - לבטא את המרחק בקילומטרים.
מטרת מדרגה 2 לבעיית מטרה 1
- התמודדות עם מורכבות הסרטוט שבבעיית המטרה:
תרגום הבעיה מתלת-ממד לדו-ממד באמצעות תרשים (מעגל במקום כדור). - התמודדות עם המורכבות של דרך הפתרון:
- לסמן את הנתונים על התרשים.
- להפנות תשומת לב של תלמידים למידע המופיע בתיאור הסיטואציה, לגבי מרחקו של הצופה ממרכז כדור הארץ.
הבנת המידע הזה [אדם שעומד באופן אנכי מהווה המשך לרדיוס כדור הארץ] מהווה שלב חשוב בתהליך הפתרון של בעיית המטרה.
- מעבר בין יחידות אורך שונות.
בתאריך 24 באוקטובר 2014 אלן יוסטס (Robert Alan Eustace) סגן נשיא בכיר בחברת גוגל, קבע את שיא העולם לנפילה חופשית מגובה של כ-41 ק"מ.
אלן שבר את השיא הקודם שנקבע בתאריך 14 באוקטובר בשנת 2012 על ידי פליקס באומגרטנר האוסטרי, שצנח מגובה של כ- 38 ק"מ.
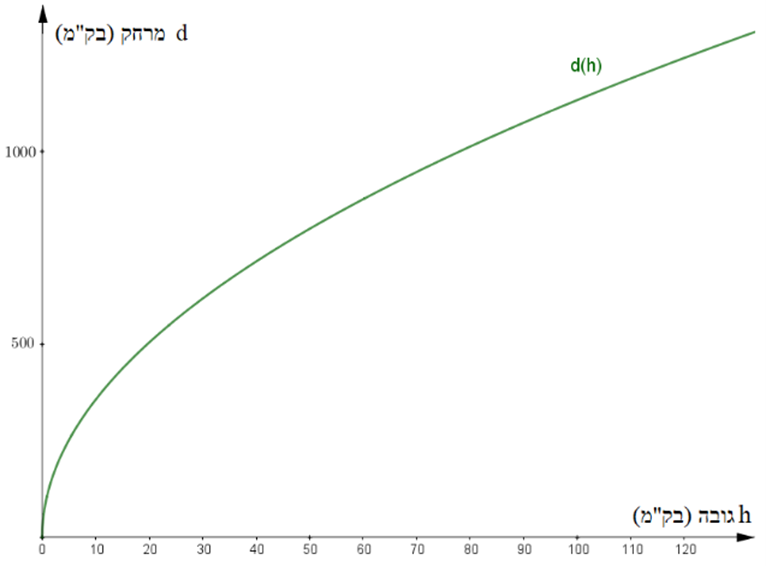
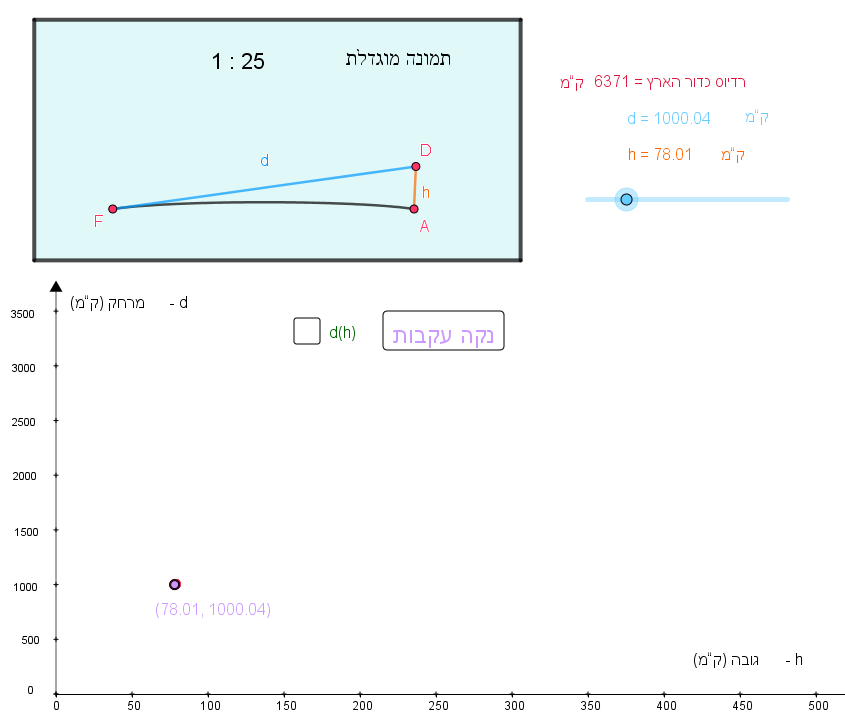
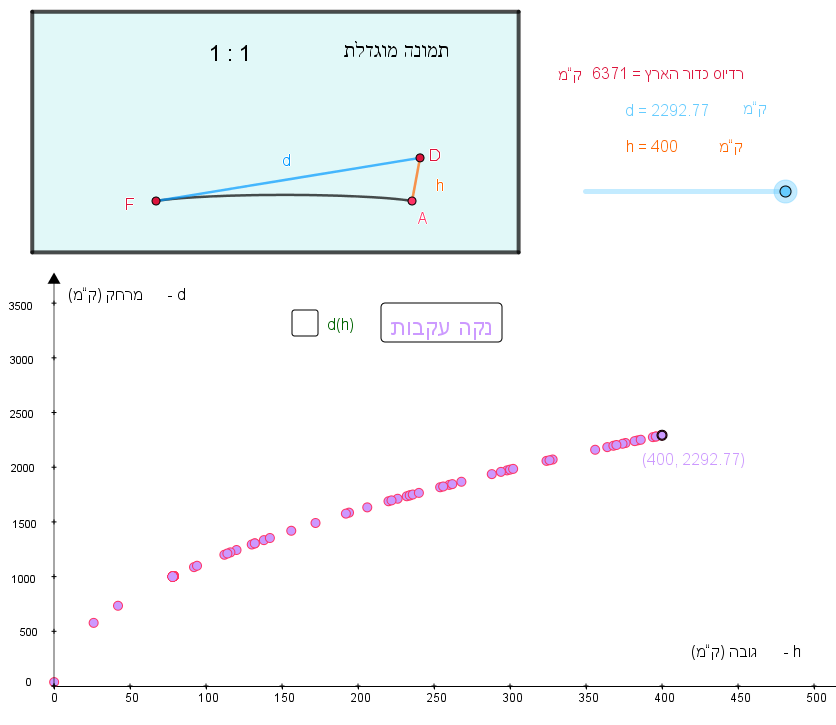
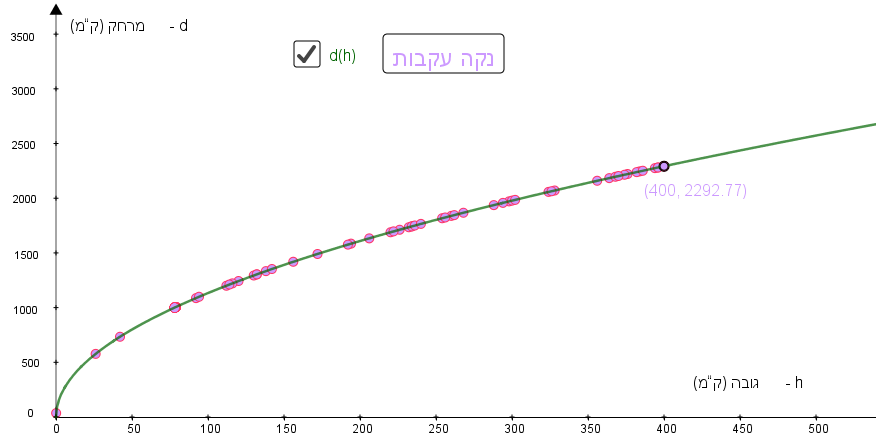
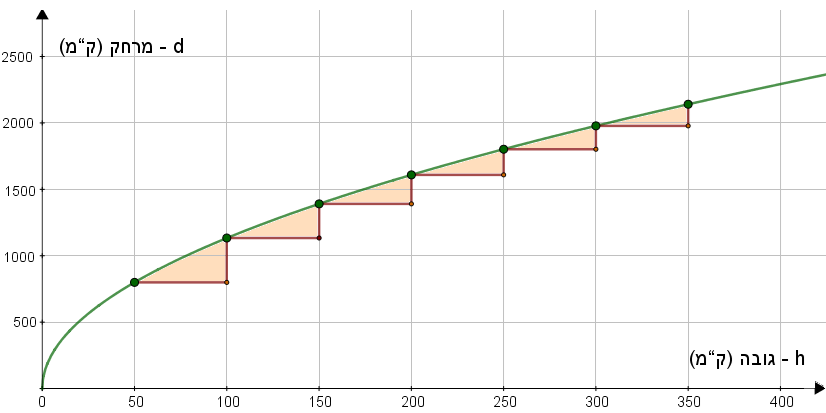
נתון גרף הפונקציה \(d(h)\) המתארת מרחקו של צופה אל קו האופק d (בק"מ), כפונקציה של גובה עין של הצופה h (בק"מ) מעל פני כדור הארץ.
- תארו לפחות שתי תכונות שונות של הפונקציה \(d(h)\) בהסתמך על הגרף.
כיצד תכונות אלה באות לידי ביטוי בחיי היומיום?
\(\space\) - סמנו על גרף הפונקציה שתי נקודות המתארות את שני השיאים של צניחה לעבר הקרקע.
שערו בכמה רחוק יותר (בערך) המרחק שראה אלן יוסטס את קו האופק, מאשר המרחק שראה פליקס באומגרטנר את קו האופק.
בדקו את תשובתכם ביישומון.
\(\space\) - באיזה גובה צריך להיות צופה, כדי לראות את קו האופק במרחק של כ-1,000 ק"מ?
בדקו את החישובים שלכם ביישומון.
\(\space\) - אילו שאלות נוספות אפשר לשאול ?
תוכלו לקרוא את הכתבה "נגע בשמיים: שיא חדש לקפיצה מקצה החלל", שפורסמה באתר ynet בתאריך 25.10.14.
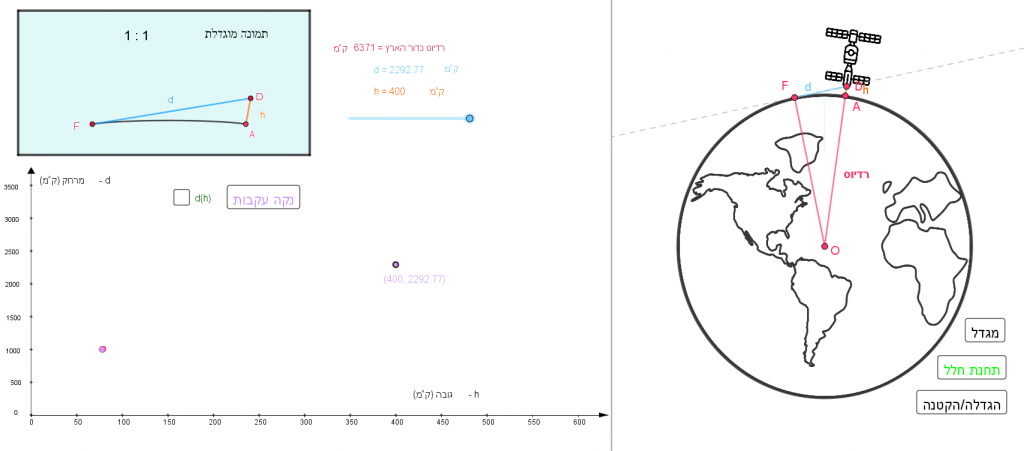
בחלון הימני:
- לחיצה על הכפתורים "מגדל" או "תחנת חלל" מדגימה את הגובה של הצופה, ומשנה בהתאם, בחלון השמאלי, את:
- הערכים בסרגל הגרירה
- הנקודה שעל הפונקציה
- לחיצה על "הגדלה/הקטנה" מציגה את פני הכדור בהתאם.
בחלון השמאלי:
- סמנו את \(d(h)\) כדי להציג את פונקציית המרחק.
- גררו את הנקודה בסרגל הגרירה, כדי לראות ערכים שונים של h ו-d.
- בתמונה המוגדלת בפינה העליונה, תוכלו לראות בהגדלה את ההצגה של פני הכדור שבחלון הימני.
- ניתן לנקות עקבות שנוצרו עקב גרירת הנקודה על הפונקציה.
- במידת הצורך, פתרו את השאלות במדרגה 1.
הצעת פתרון לבעיית מטרה 2 – העשרה
בבעיה זו התלמידים יוכלו להסביר את ממצאיהם בהקשר לשאלה [כמה רחוק אנחנו יכולים לראות?], להסיק מסקנות נוספות ולקשר אותן לחיי היומיום.
זאת באמצעות ייצוג גרפי של הפונקציה המתארת את מרחקו של צופה אל קו האופק d (בק"מ) כפונקציית גובה הצופה h (בק"מ) מעל פני כדור הארץ.
סעיף א
תשובות אפשריות:
- תחום ההגדרה של הפונקציה \(h≥0\).
מדובר בגובה הצופה מעל פני כדור הארץ ולכן מדובר על הערכים החיוביים.
\(\space\)
ממצא זה מתאים לחיי היומיום, אבל כמובן עולות השאלות, למשל:
האם ייתכן מצב של h=0 ?
עד איזה גובה הצופה יכול להגיע?
הרי מבחינת הפונקציה אין הגבלה, אבל מבחינת חיי היומיום יש.
\(\space\)
למשל, ייתכן מצב שהצופה נמצא בתחנת חלל, כלומר בגובה של כ-400 ק"מ מעל פני כדור הארץ. האם ניתן לדבר על גובה מקסימאלי?
\(\space\) - טווח הערכים של הפונקציה הוא: \(d≥0\).
המסקנות לגבי תחום ההגדרה של הפונקציה בהקשר לסיטואציות אפשריות, עשויות להיות יעילות בתשובה לשאלה בנוגע לטווח הערכים.
הצופה שנמצא בתחנת חלל יכול לראות את קו האופק במרחק של כ-2,293 ק"מ.
\(\space\) - הפונקציה \(d(h)\) חיוביות לכל \(h>0\)
\(\space\) - הפונקציה \(d(h)\) עולה לכל \(h>0\)
ככל שהצופה נמצא גבוה יותר, כך הוא יכול לראות רחוק יותר.
\(\space\) - קצב ההישתנות של הפונקציה אינו קבוע, הוא קטן ככל ש-h גדל.
התלמידים עשויים לסמן שלוש נקודות על הגרף ולהראות כי נקודות אלה לא נמצאות על אותו הקו הישר.
סעיף ב
התלמידים מוזמנים להשתמש בידע שרכשו בפתרון בעיית מטרה 1 ובתכונה של שורש ריבועי
\(\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}\hspace{0.5 cm} (a≥0\space , \space b≥0)\)
כדי להעריך כי אלן יוסטס אכן רואה את קו האופק יותר רחוק מפליקס באומגרטנר ולחשב בקירוב (או להשתמש באומדן) בכמה:
\(d_{ןלא} \space \approx \sqrt{2 \cdot 64 \cdot 10^5 \cdot 41} \space\approx\space 1600\sqrt{205}\)
\(d_{סקילפ} \space \approx \sqrt{2 \cdot 64 \cdot 10^5 \cdot 38} \space\approx\space 1600\sqrt{190}\)
התלמידים מוזמנים להשתמש ביישומון, המאפשר לחקור את התופעה באמצעות סימון נקודות במערכת הצירים, כאשר כל נקודה, מתאימה לגובה הצופה את מרחק הראיה אל קו האופק.
סעיף ג
התלמידים עשויים לפנות לביטויים אלגבריים [ייתכן וביטויים אלה כבר עלו בפתרון של בעיית המטרה 1]:
\(d\approx \sqrt{2R}\cdot \sqrt{h}\)
\(\Downarrow\hspace{1cm}\)
\(h\approx\large\frac{d^2}{2R}\)
ולחשב את הגובה המתאים לנתון: ק"מ 78 \(h \space\approx\).
לפניכם סקיצה המתארת את הסיטואציה של מרחק צופה מקו האופק.
המעגל שמרכזו בנקודה O מייצג את כדור הארץ.
הנקודות O, B ו-C נמצאות על קו ישר אחד.
נניח כי רדיוס כדור הארץ הינו 6,371 ק"מ = R.
- השלימו את השוויון והסבירו: _______________\(R^2+d^2=\)
כתבו ביטויים שווי ערך לביטוי זה.
\(\space\) - רוצים להגדיל פי 2 את מרחקו של הצופה מקו האופק.
פי כמה בערך יש להגדיל את גובה עיניו של הצופה מעל פני כדור הארץ?
שימו לב: סקיצה משמע סרטוט לא מדויק,
כך למשל, במציאות, רדיוס כדור הארץ (R)
גדול בהרבה יותר מגובה העיניים של הצופה (h).
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 2.
- במידת הצורך, פתרו את השאלות במדרגה 2.
הצעת פתרון למדרגה 1 של בעיית מטרה 2
בעיה 2.1.1
סעיף א
\(R^2+d^2=(R+h)^2\)
\(R^2+d^2=R^2+2Rh+h^2\)
\(d^2=2Rh+h^2\)
\(d=\sqrt{2Rh+h^2}=\sqrt{h(2R+h)}\)
סעיף ב
ערכו של h קטן בהרבה מערכו של R, עד לזניח, ולכן ניתן לרשום כי \(d \approx \sqrt{2Rh}\).
לכן, כדי להגדיל פי 2 את מרחקו של הצופה מקו האופק, יש להגדיל פי 4 את גובה עיניו של הצופה מעל פני כדור הארץ.
מטרת מדרגה 1 לבעיית מטרה 2
- התמקדות בפיתוח ביטוי אלגברי המתאר את הקשר בין מרחקו של צופה אל קו האופק d (בק"מ), לבין גובה עין של הצופה h (בק"מ), מעל פני כדור וכתיבת ביטויים שווי ערך.
- הסקת מסקנות בהסתמך על הביטוי האלגברי.
הצעת פתרון למדרגה 2 של בעיית מטרה 2
בעיה 2.2.1
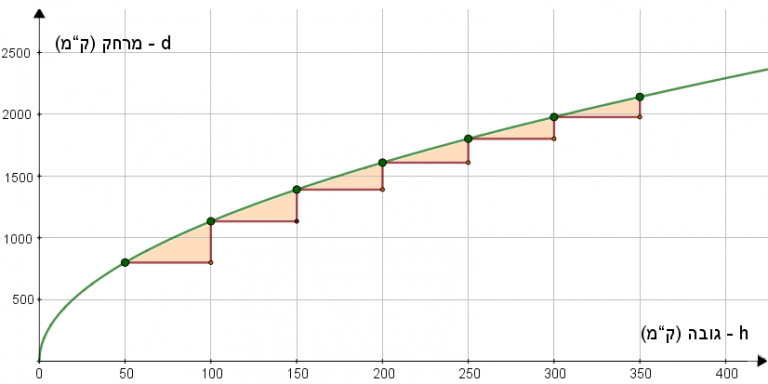
לפי המדרגות המופיעות בתרשים, התלמידים עשויים לזהות כי קצב ההישתנות של הפונקציה \(d(h)\) אינו קבוע. הוא קטֵן ככל ש-h גדל.
בנוסף, יהיו אולי תלמידים שיציעו לחשב את שיעור ה-y של חלק מהנקודות המסומנות ולהראות כי נקודות אלה לא נמצאות על אותו הקו הישר.
מטרת מדרגה 2 לבעיית מטרה 2
- התמקדות בייצוג גרפי של הפונקציה \(d(h)\) המתארת מרחקו של צופה אל קו האופק d (בק"מ), כפונקציה של גובה עין של הצופה h (בק"מ), מעל פני כדור הארץ.
- הסקת מסקנות בהסתמך על ייצוג הגרפי ובעיקר לגבי קצב ההישתנות של הפונקציה.
3. נספח למדריך למורה
1. המלצה לפתיח השיעור: כמה רחוק קו האופק?
מומלץ לתת לתלמידים משימה – לפני השיעור העוסק באשכול "כמה רחוק קו האופק?" – לחפש במקורות מידע דברים מעניינים הקשורים למושגים המרכזיים הקשורים לאשכול (כמו שקיומו של קו האופק נובע מעקמומיות פני כדור הארץ, מודל כדור הארץ עצמו).
לכאורה מושגים אלה נראים מוכרים מחיי היומיום ומובנים מאליהם לתלמידים, אך למעשה ייתכן וצפויות הפתעות בדרך.
כך למשל, אחת ההפתעות קשורה לרקע ההיסטורי: הרי כבר בעת העתיקה חשבו היוונים הקדמונים כי הארץ היא כדור עגול. על מה הם ביססו את דעתם זו? מה חשבו על כך פיתגורס, אפלטון ואריסטו ומלומדים בימי הביניים? ראו למשל, קישור 1 , קישור 2. כיצד התפתח המדע? ומה קורה בימינו?
בכלים מודרניים נקבע שצורת הארץ מקורבת לצורת כדור, עד כדי סטייה אליפטית זעירה. צורת אליפסואיד בעל "פיחוס" (flattening) של 1/300, אף תואמת יותר את צורתה המדויקת של הארץ.
מומלץ לערוך דיון בתחילת השיעור סביב הגילויים של התלמידים והמקורות שיביאו.
2. המלצה לשאלות נוספות
מומלץ לעודד שאילת שאלות נוספות סביב הממצאים שקיבלו. למשל:
- גובה הצופה כ- 380 ק"מ מעל קרקע – איפה נמצא הצופה?
ממצא זה יכול להתאים למצב שהצופה נמצא בתחנת החלל. - מה הקשר בין מרחק הצופה לקו האופק לבין גובה הצופה מהקרקע? הנוסחה \(d\space\approx\space\sqrt{2Rh}\) שקיבלו עשויה לתת לתלמידים תשובה לשאלה זו.
הדבר עשוי לעודד שאלות נוספות. למשל, האם וכיצד ניתן ליצור מצב שהצופה יראה רחוק יותר? כלומר, לאיזה גובה הוא צריך לעלות בשביל לראות במרחק גדול יותר ממה שהוא נמצא כעת.
אפשר לשאול שאלות כלליות יותר, למשל פי כמה יש להגדיל h כדי שמרחק הצופה מקו האופק יגדל פי 2?
3. המלצות לשימוש ביישומון בפתרון בעיית מטרה 2
היישומון מציע לתלמידים אפשרויות נוספות שעשויות להעשיר את השיעור ולתת היבטים נוספים הקשורים לסיטואציה ולקשר למתמטיקה:
"משולש" ADF
ניתן לראות את "משולש" ADF גם בחלון הימני ביישומון (המזכיר את התרשים המופיע בתיאור הסיטואציה שבבעיית מטרה 1). גם בחלון השמאלי של היישומון, הוא מופיע בהגדלה מעל מערכת הצירים.
הופעתו של ה"משולש" עשויה לקשר בין החישובים שנעשו בפתרון בעיית מטרה 1, פיתוח הנוסחה לחישוב מרחק לקו האופק (ייתכן והביטוי התקבל כבר בבעיית מטרה 1) לבין החקר המבוסס על הייצוג הגרפי של הפונקציה \(d(h)\) בבעיית מטרה 2.
בנוסף, הדבר עשוי לזמן את הדיון (אם עדיין לא נעשה) לגבי העקמומיות של כדור הארץ, הגובה המקסימאלי (והמינימאלי) האפשרי מבחינת ההתייחסות לחיי היומיום. זאת לעומת תכונות הפונקציה \(d(h)\space=\space\sqrt{h(2R+h)}\space\approx\space\sqrt{2Rh}\) בשני ייצוגיה – האלגברי והגרפי.
שימוש בסרגל גרירה כדי:
- לבדוק את החישובים של תלמידים באמצעות היישומון,
למשל, בסעיף ג בבעיית מטרה 2 בעזרת סרגל הגרירה התלמידים יכולים למצוא (בקירוב) את ערכו של 78.01 ק"מ \(h\space\approx\), המתאים למרחק הנתון של 1,000 ק"מ \(d\space\approx\).
- הצגת נקודות במערכת צירים המייצגות מרחק צופה לקו האופק (d) בהתאם לגובה עיניו מעל פני כדור הארץ (h).
- הצגת עקבות
הצגת גרף הפונקציה \(d(h)\) והבחנה כי:
- כל הנקודות שהתקבלו בבחירת ערכים שונים של h נמצאות על גרף הפונקציה.
- הפונקציה מוגדרת לכל ערכי \(h≥0\), אבל סרגל הגרירה מגביל את הערכים של \(0<h≤400\)
- האם יש בכך הגיון מבחינת חיי היומיום או שזוהי רק המגבלה הטכנית של היישומון?
