אשכול תכנון ביקור בגן החיות של ווינה – למורה
יישומונים
- – – – – –
- יישומון למדרגה 1
- – – – – –
- – – – – –
- – – – – –
הנחיות למורה
כיתה מומלצת:
כיתה ח / כיתה ט
נושאים מתמטיים:
קנה מידה, אומדן של אורך קטעים בסקיצה של מפה, אורך קשת, מהירות, תכנון זמנים.
נושא חוץ־מתמטי:
קריאת מפה, ביקור בגן חיות
משך הזמן:
30-45 דקות
ידע ומיומנויות הנדרשים לפתרון המשימה:
- שימוש בקנה מידה לחישוב אורכי קטעים ואורך קשת במציאות
- חישוב היקף של מעגל ואורך קשת
- אומדן של אורך קטעים במפה, כשלא סביר לחשב את אורכם במדויק.
- יחידות שונות למדידת מהירות ומעברים בין היחידות
- קשר בין זמן, דרך ומהירות.
| נושא | מושגים | מיומנויות |
|---|---|---|
| קנה מידה | – קנה מידה – גודל במציאות – גודל בסרטוט – יחידות אורך | – מציאת קנה מידה על פי מידות נתונות בסרטוט ובמציאות. – מציאת גודל במציאות על פי קנה מידה והגודל שנמדד בסרטוט. |
| אומדן | – אומדן – אורך דרך | – יש למדוד ולאמוד אורך של קטעים בסרטוט. |
| היקף מעגל אורך קשת | – מרכז מעגל – רדיוס – היקף מעגל | – יש לחשב אורך קשת על פי היקף מעגל והזווית המתאימה לקשת. |
| בעיות אורייניות מתוך מציאות קרובה לתלמידים | – אורך דרך – מהירות – אומדן – זמן הגעה | – פתרון בעיות המשלבות בין הבנת טקסט וקריאת סרטוט סכמתי של מפה לבין חישובים של אורך דרך, מהירות וזמן. |
ישומונים:
יש
מטרות האשכול:
- פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך.
הפתרון מוביל להעמקת ההבנה כיצד להיעזר במפה, בקנה מידה ובנוסחה \(s=v\cdot t\) כדי לתכנן ביקור בגן חיות. - פתרון הבעיות שבאשכול תורם לפיתוח היכולת לפתור בעיות מורכבות המשלבות נושאים מתוכנית הלימודים באלגברה ובגיאומטריה.
מערך דידקטי מומלץ:
- רצוי, לפני הצגת האשכול, להקדים ולשאול את התלמידים שאלות שתלמדנה על הידע שלהם לגבי קנה מידה, למשל: באילו הקשרים מופיע קנה מידה? איך נעזרים בו? מה ההבדל בין קנה מידה שמופיע במפות המודפסות על נייר לבין מפות המופיעות במחשב?
- בתחילת האשכול ישנם קישורים המפנים לקטעי ווידאו של הרכבת הפנורמית בגן החיות בווינה ושל דובי הפנדה בגן חיות זה. ניתן לצפות בקטעים אלה כדי להכניס את התלמידים לאווירה של ביקור בגן החיות.
ארגון הכיתה:
למידה בזוגות או בקבוצות.
ציוד נדרש:
מחשבון, מחשב כדי שניתן יהיה להפעיל את קטעי הווידאו והיישומון (לא הכרחי), חוט (או שרוך) שיכול לעזור בחישוב אומדן לאורך מסלול הרכבת, סרגל.
ניהול השיעור:
המורה יאפשר לתלמידים לפתור את הבעיות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות וביישומון. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי־הבנות.
המורה יבקש, מתלמידים שסיימו לפתור את הבעיות שבאשכול, להציע שאלה נוספת הקשורה לאשכול ולפתור אותה.
דיון בכיתה:
- התלמידים יציגו ויסבירו את תשובותיהם בדיונים. רצוי לאפשר להם להציג דרכים שונות לפתרון. כמו: דרכים שונות לאמוד את אורך מסלול הרכבת.
- בדיון בכיתה רצוי לאפשר לתלמידים להציג את השאלות הנוספות שחשבו עליהן ולדון בפתרונות שהציעו.
המורה יכול/ה לבחור, מבין שאלות התלמידים, את השאלות שלדעתו/ה ראוי לדון בהן. - אפשרות נוספת היא להציע לתלמידים להגיש את השאלות הנוספות ואת פתרונן כעבודת הגשה.
דנה ומשפחתה מתכננים ביקור בגן החיות של ווינה, בירת אוסטריה.
גן חיות זה בנוי כחלק מפארק שנברון ונחשב לעתיק ביותר בעולם שעדיין פעיל ופתוח למבקרים.
גן החיות הוקם כמתחם מלכותי ב-31 ביולי 1752. מאז הקמתו עבר שינויים רבים, אולם הוא עדיין פעיל במקום בו הוקם. את גן החיות יסד הקיסר פרנץ הראשון, אשר רצה להקים גן חיות מלכותי במושב הקיץ שלו.
דנה קראה שבגן החיות בווינה ניתן לצפות בדובי פנדה.
קטע ווידאו של דובי הפנדה בגן החיות בוינה: https://www.youtube.com/watch?v=4OggTSf8x8I
רק 49 דובי פנדה חיים כיום מחוץ לגבולות סין, ב-18 גני חיות המתפרשים על 13 מדינות בלבד.
לפניכם מפה של גן החיות (השטח הצהוב).
תמונה 1
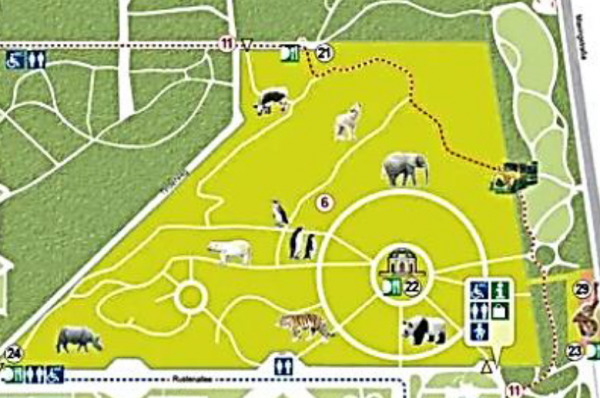
סקיצה 1 היא סרטוט סכמתי של גן החיות.
סקיצה 1
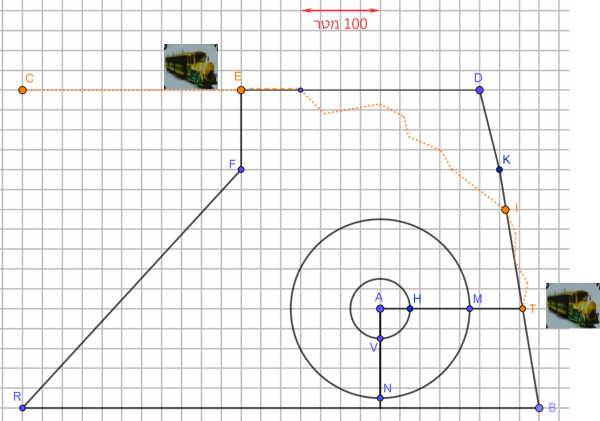
מסלולי הליכה בסקיצה מסומנים על ידי קו רציף 
בפארק שנבורן ישנה רכבת פנורמית.
מסלול הרכבת בסקיצה מסומן על ידי קו לא רציף 
קטע ווידאו של הרכבת בגן החיות בווינה: https://www.youtube.com/watch?v=ULfbXkPdgXc
כדי לתכנן את הביקור בגן החיות, הסתכלה דנה בסקיצה של גן החיות, ביררה מתי מאכילים את דובי הפנדה וכן, מהו לוח הנסיעות של הרכבת הפנורמית שבפארק.
דנה מצאה ש:
- ניתן לצפות בדובי הפנדה מנקודות V או N המסומנות בסקיצה 1.
\(\space\) - האכלת דובי הפנדה מתקיימת פעמיים ביום: בשעה 10:00 ובשעה 14:00.
\(\space\) - הרכבת יוצאת מתחנה C כל 45 דקות החל משעה 9:30.
\(\space\) - תחנות הרכבת הפנורמית מסומנות בסקיצה 1 על ידי האותיות: C, E, I, T.
\(\space\) - הרכבת עוצרת בכל תחנה למשך 3 דקות.
\(\space\) - מהירות הרכבת 10 קמ"ש.
דנה ומשפחתה החליטו לעלות על הרכבת בתחנה שבנקודה C, לרדת בתחנה T ומשם להמשיך ללכת ברגל, בדרך הקצרה ביותר, כדי להגיע לאזור המחייה של דובי הפנדה ולצפות בהאכלתם.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
סקיצה 1
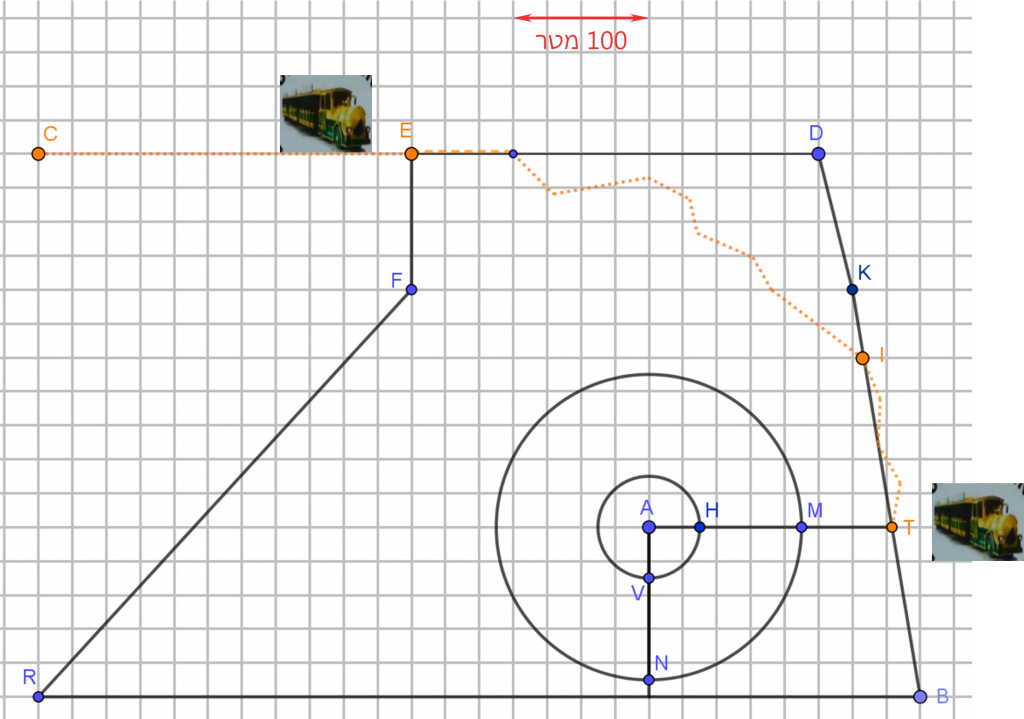
פתרון לבעיית מטרה 1
קנה המידה הוא: אורך צלע של משבצת אחת מתאים ל- 25 מטר במציאות.
אומדן של אורך מסלול הרכבת מתחנה C לתחנה T: כ- 800 מטר.
זמן נסיעת הרכבת: \(\Large\frac{800\space\cdot\space60}{10\space\cdot\space1,000}\normalsize=תוקד\space4.8\)
ולכך יש להוסיף 6 דקות של התעכבות הרכבת בתחנות E ו- I,
סך-הכל: כ- 10.8 דקות.
הדרך הקצרה ביותר כדי להגיע מנקודה T לנקודה בה ניתן לצפות בדובי הפנדה היא:
מ- T ל- H ומשם לנקודה V דרך קשת HV.
מרחק הליכה מנקודה T לנקודה H ומשם לנקודה V:
\(5.5\cdot25+\Large\frac{3\space\cdot\space\pi\space\cdot\space25}{4}\normalsize=רטמ\space196.4\)
\(\space\)
זמן הליכה: כ- \(\Large\frac{196.4\space\cdot\space60}{3\space\cdot\space1,000}\normalsize=תוקד\space3.9\)
\(\space\)
כלומר, זמן ההגעה מנקודה C לנקודה V, הוא בסך הכל כ- 15 דקות.
אם דנה ומשפחתה יעלו על הרכבת היוצאת בשעה 9:30, הם יגיעו בסביבות השעה 9:45 לנקודה V ויהיה עליהם לחכות כרבע שעה כדי לצפות בהאכלת דובי הפנדה.
הרכבת היוצאת מתחנה T סמוך לשעה 14:00, יוצאת בשעה 13:15 (מ-9:30 עד 12:30 עוברות 3 שעות שהן \(4\space\cdot\space45\) דקות, והרכבת הבאה יוצאת כעבור 45 דקות כלומר בשעה 13:15)
אם דנה ומשפחתה יעלו על הרכבת היוצאת בשעה 13:15, הם יגיעו ערך בשעה 13:30 ויהיה עליהם לחכות כחצי שעה להאכלת דובי הפנדה.
לכן כדאי שיעלו על הרכבת היוצאת בשעה 9:30.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- לסרטוט וסימון קטע יש לבחור את
בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. - לסימון נקודה יש לבחור את
בסרגל הכלים, ואז לסמן את הנקודה על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. - במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
הצעת פתרון למדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
האומדן הקרוב ביותר לאורך הדרך מ- C ל- T הוא כ- 800 מטר.
מטרת מדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
הבעיה מאפשרת להבין שיש לאמוד את אורך מסלול הרכבת, ואין צורך לחשב אותו במדויק. וכן, מאפשרת לבחור את התשובה המתאימה מבין 4 תשובות נתונות.
היישומון המצורף מאפשר לסמן נקודות ולהעביר קטעים בסקיצת המפה של גן חיות.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 3.
סקיצה 1
הצעת פתרון למדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
מרחק הליכה מנקודה T לנקודה H ומשם לנקודה V:
\(5.5\cdot25+\Large\frac{3\space\cdot\space\pi\space\cdot\space25}{4}\normalsize=רטמ\space196.4\)
\(\space\)
מרחק הליכה מנקודה T לנקודה A ומשם לנקודה V:
\((7+1.5)\cdot25=רטמ\space212.5\)
\(\space\)
מרחק הליכה מנקודה T לנקודה N ומשם לנקודה V:
\(2.5\cdot25+\Large\frac{2\space\cdot\space4.5\space\cdot\space\pi}{4}\normalsize\cdot\space25=רטמ\space239.2\)
\(\space\)
לכן הדרך הקצרה ביותר היא מנקודה T לנקודהH ומשם לנקודה V.
מטרת מדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
הבעיה ממקדת את תשומת הלב שישנן כמה דרכים ללכת בהן כדי לצפות בדובי הפנדה, ויש לבחור בדרך הקצרה ביותר.
1.3 מדרגה 3 לבעיית מטרה 1
בעיה 1.3.1
דנה רוצה לחשב את זמן ההליכה מנקודה T לנקודה H. הניחו שמהירות ההליכה היא 3 קמ"ש.
קבעו אילו חישובים מבין החישובים הבאים הוא נכון ובאילו יחידות נמדד הזמן בכל אחד מהחישובים הנכונים.
- \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5}{3}\)
\(\space\) - \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5}{3,000}\)
\(\space\) - \(\space\)\(\space\)\(\space\)\(\Large\frac{0.15\space\cdot\space60}{3}\)
\(\space\) - \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5\space\cdot\space60}{3,000}\)
\(\space\) - \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5}{3\space\cdot\space60}\)
\(\space\) - \(\space\)\(\space\)\(\space\)\(\Large\frac{150\space\cdot\space60}{3,000}\)
נמקו תשובתכם.
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית מטרה 1.
סקיצה 1
הצעת פתרון למדרגה 3 של בעיית מטרה 1
בעיה 1.3.1
התשובות הנכונות הן:
סעיף ב’ \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5}{3,000}\) בשעות,
\(\space\)
וסעיף ד’ \(\space\)\(\space\)\(\space\)\(\Large\frac{137.5\space\cdot\space60}{3,000}\) בדקות.
מטרת מדרגה 3 של בעיית מטרה 1
בעיה 1.3.1
הבעיה ממקדת את תשומת הלב לצורך להתאים את היחידות של המהירות, כדי שניתן יהיה לחשב זמן. מהירות הרכבת ומהירות ההליכה נתונות ב-קמ"ש, קנה המידה מתייחס למטרים, לכן חישוב אורכי המסלולים הוא במטרים.
בבעיה נתונות כמה תשובות המתייחסות לדרכים שונות לחישוב הזמן (בשעות או בדקות) ולטעויות אפשריות הן במעבר בין היחידות של מהירות והן בחישוב אורך הקטע TH.
יש לבחור בתשובות הנכונות.
- ניתן לצפות בדובי הפנדה מנקודות V או N המסומנות בסקיצה 1.
\(\space\) - האכלת דובי הפנדה מתקיימת פעמיים ביום: בשעה 10:00 ובשעה 14:00.
\(\space\) - הרכבת יוצאת מתחנה C כל 45 דקות החל משעה 9:30.
\(\space\) - תחנות הרכבת הפנורמית מסומנות בסקיצה 1 על ידי האותיות: C, E, I, T.
\(\space\) - הרכבת עוצרת בכל תחנה למשך 3 דקות.
\(\space\) - מהירות הרכבת 10 קמ"ש.
סקיצה 1
הצעה לבעיה נוספת
לפניכם הצעה לבעיה נוספת אותה ניתן להציע לתלמידים שסיימו לפתור את הבעיות שבאשכול, כשיעורי בית או כעבודת הגשה:
באשכול נתון כי:
רק 49 דובי פנדה חיים כיום מחוץ לגבולות סין, ב־18 גני חיות המתפרשים על 13 מדינות בלבד.
אילו טענות מבין הטענות הבאות נכונות:
- מבין 18 גני החיות, שהוזכרו לעיל, יימצא גן חיות אחד שחיות בו לפחות 4 פנדות.
- מבין 13 מדינות, שהוזכרו לעיל, תימצא מדינה אחת שחיות בה לפחות 4 פנדות.
- מבין 13 מדינות, שהוזכרו לעיל, יכולה להימצא מדינה אחת שיש בה 7 גני חיות שבהם יש פנדות.
הסבירו תשובתכם.