אשכול דמיון בעדשות חלק א - למורה
הנחיות למורה
אשכול 1 מתוך 3 אשכולות.
יחידה:
מדע – אופטיקה
כיתה מומלצת:
כיתה ח / כיתה ט / כיתה י
משך הזמן המומלץ:
45-90 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
- עדשה מרכזת, מוקד עדשה, מהלך קרני אור העוברים דרך עדשה מרכזת, דמות אופטית וסרטוטה, דמות ממשית.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| דמיון משולשים | – משולשים דומים – יחס בין צלעות משולשים – פרופורציה | – זיהוי משולשים דומים שבהם לכל זווית במשולש אחד, יש זווית ששווה לה במשולש אחר. – מציאת יחס בין צלעות מתאימות במשולשים דומים. – מציאת נתונים חסרים מתוך תכונות הדמיון ותוך שימוש בפרופורציה. |
| חפיפת משולשים | – יחס דמיון שווה ל- 1 – משפטי חפיפה | – זיהוי משולשים חופפים. – הסקת מסקנות לגבי צלעות שוות במשולשים חופפים. |
| בעיות אורייניות מתוך מציאות | – עדשה מרכזת – מוקד – דמות אופטית | – פתרון בעיות המשלבות בין הבנת טקסט מילולי, המסביר את מהלך קרני האור העובר דרך עדשה מרכזת, לבין הידע המתמטי של תלמידים, בנושא דמיון משולשים. |
מטרת האשכול:
ידע מתמטי של דמיון משולשים, מאפשר להבין במה תלוי היחס בין גודל העצם לגודל הדמות של העצם, המשתקפת דרך עדשה מרכזת, ולחשב יחס זה.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
העמקה בנושא דמיון משולשים.
שלב הלמידה המומלץ:
בכיתה ח – סיכום של נושא דמיון משולשים.
בכיתה ט – לקראת סוף השנה, כחזרה וכהכנה לכיתה י'.
מערך דידקטי מומלץ:
ארגון הכיתה:
- ניתן לפתוח את השיעור בהקרנת אחד, או יותר, מקטעי הווידאו שכתובתם נמצאת בתחילת האשכול.
או, לחילופין, ניתן לבצע את הניסויים המתוארים בקטעי הווידאו (כל מה שצריך: כוס בצורת גליל ומים) ולבקש מהתלמידים להעלות שאלות הנובעות מניסויים אלה. - ארגון הכיתה בקבוצות של 2-4 תלמידים.
- התלמידים יקראו את תיאור הסיטואציה.
הערה: בהקדמה נשאלת השאלה מדוע הנוף המשתקף דרך העדשה הקמורה הוא מוקטן והפוך. אין צורך לענות על כך בשלב זה. השאלה היא כדי לעורר סקרנות. - דיון כיתתי קצר המבהיר את המושגים, ואת מהלך סרטוט דמות אופטית של עצם המשתקפת דרך עדשה מרכזת דקה.
- התלמידים פותרים את בעיית מטרה 1, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול.
- דיון כיתתי בו התלמידים מציגים את תשובותיהם ומסבירים אותן.
- התלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
שאלות מומלצות לדיון כיתתי:
- כיצד ניתן לדעת שיש להיעזר בדמיון משולשים כדי לפתור את בעיית המטרה?
- כיצד ניתן לזהות את המשולשים הדומים בסרטוט המורכב?
- האם משולשים חופפים הם משולשים דומים?
- במה עוזרת לנו המתמטיקה כדי להבין את המציאות, בהקשר לאשכול זה?
אשכול דמיון בעדשות חלק א
בתמונה שלפניכם הנוף משתקף דרך עדשה קמורה.
כפי שניתן להבחין, הדמות של הנוף (ההשתקפות) היא מוקטנת והפוכה.
מדוע?
בתמונה משמאל, דמות הנר המשתקפת דרך העדשה, נראית על הקיר והיא מוגדלת והפוכה.
מדוע?
תיאור סיטואציה
עדשה היא אלמנט אופטי המורכב מחומר שקוף ובעלת מבנה הנדסי מיוחד.
כאשר קרני האור עוברות מהאוויר לחומר אחר הן נשברות (משנות את כיוונן).
מבנה העדשה גם הוא משפיע על מסלול קרני האור העוברות דרכה.
עדשות משמשות בדרך כלל ליצירת דמות אופטית מוגדלת או מוקטנת של עצם כלשהו.
מבחינים בין שני סוגים של עדשות: עדשות קמורות ועדשות קעורות.
עדשות קמורות הן עדשות שעבות במרכזן ודקות בקצותיהן.
עדשות קעורות הן עדשות שדקות במרכזן ועבות בקצותיהן.
עדשה דו-קמורה
עדשה דו-קעורה
נהוג לסמן עדשה קמורה דקה (מרכזת) כך:
באשכול זה נתרכז בעדשות דו קמורות סימטריות.
מהלך קרני אור דרך עדשה קמורה
עדשה קמורה מרכזת או אוספת את קרני האור המקבילות העוברות דרכה אל נקודה אחת. היא המוקד הראשי של העדשה המסומן באות F.
לעדשה קמורה יש שני מוקדים ראשיים, אחד מכל צד.
בעדשה קמורה דקה, המרחקים בין כל אחד מהמוקדים למרכז העדשה שווים זה לזה. מרחק זה מסומן באות \(f\).
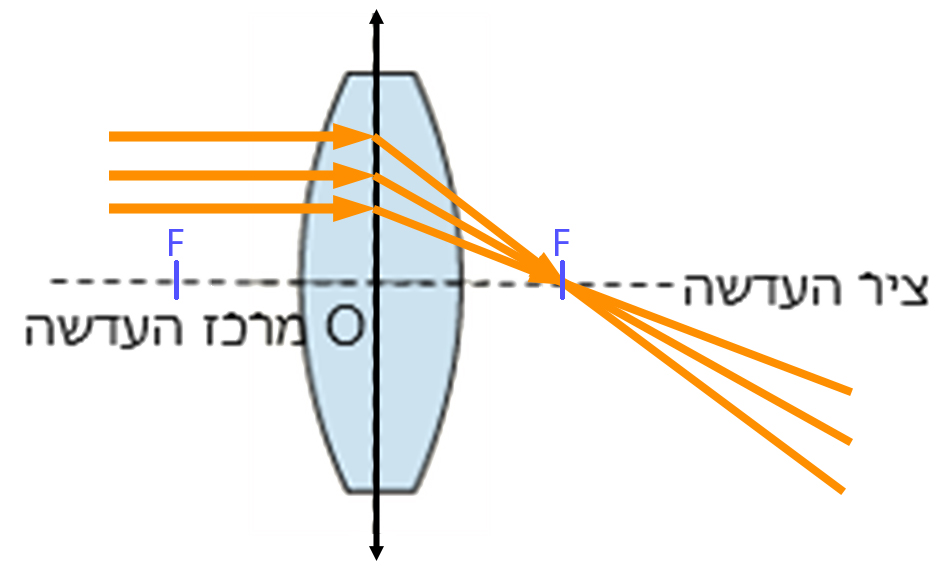
התבוננו בצילום משמאל.
על המסך (קיר) מתקבלת דמות הפוכה ומוגדלת של הנר.
מהלך קרני האור וסרטוט הדמות
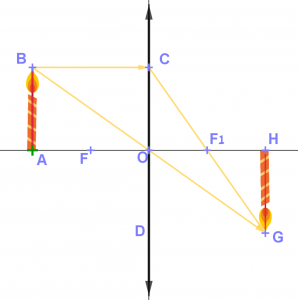
בסרטוט למטה נקודה O היא מרכז העדשה. AH הוא ציר העדשה.
להבת הנר (AB) מאונכת לציר העדשה (AH).
הדמות האופטית של להבת הנר (GH) מאונכת לציר העדשה AH.
קרן האור BC מקבילה לציר העדשה, פוגעת בעדשה, נשברת ועוברת דרך המוקד F1.
קרן האור BO עוברת דרך מרכז העדשה ואינה נשברת.
שתי הקרניים נפגשות בנקודה G.
HG זו הדמות האופטית של להבת הנר.
היעזרו ביישומון המצורף, להבנת הקשר בין הניסוי (המצב במציאות) למודל הגיאומטרי.
- לחיצה על "ניסוי" מגלה/מסתירה את צילום הנר והעדשה.
- לחיצה על "מודל גאומטרי" מגלה/מסתירה את סרטוט קרני האור דרך העדשה.
1. בעיית מטרה 1
נר משתקף דרך עדשה קמורה דקה.
הנר ודמות הנר מאונכים לציר העדשה.
קרן האור BC מקבילה לציר העדשה.
מרחק המוקד ממרכז העדשה הוא 2 ס"מ.
- אם נתון שהיחס בין אורך הנר לבין אורך הדמות של הנר הוא 3:1, אז חשבו:
- את המרחק של הדמות של הנר ממרכז העדשה.
- את המרחק של הנר ממרכז העדשה.
- את היחס בין מרחק הנר ממרכז העדשה לבין מרחק המוקד ממרכז העדשה.
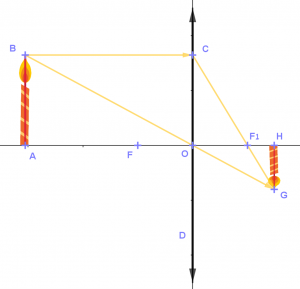
- אם נתון שהיחס בין אורך הנר לבין אורך הדמות של הנר הוא 1:2, אז חשבו את היחס בין מרחק הנר ממרכז העדשה לבין מרחק המוקד ממרכז העדשה.
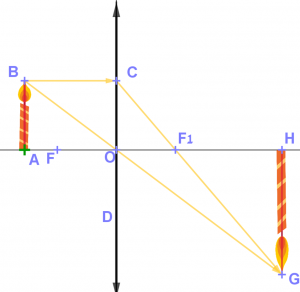
- אם נתון שהיחס בין אורך הנר לבין אורך דמות הנר הוא 1:1, אז חשבו את היחס בין מרחק הנר ממרכז העדשה לבין מרחק המוקד ממרכז העדשה.
בכל הסעיפים תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון בעיית מטרה 1
סעיף א
נתון כי: \(AB\perp AH\)
\(HG\perp AH\)
\(BC ∥ AH\)
\(OF=OF_1=מ"ס\space\space 2\)
\(\Large\frac{AB}{HG}\normalsize=3\)
יש לחשב את: \(OH\space ,\space AO\space ,\space \Large\frac{OA}{OF}\)
פתרון:
\(\triangle {COF_1}\sim\triangle{GHF_1}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{CO}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\)
מרובע ABCO הוא מלבן
(או חפיפת משולשים BCO ו- OAB)
\(\Downarrow\hspace{1cm}\)
\(CO=AB\)
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{2}{HF_1}\normalsize=3\)
\(\Downarrow\hspace{1cm}\)
\(HF_1=מ"ס\space\Large\frac{2}{3}\)
\(\Downarrow\hspace{1cm}\)
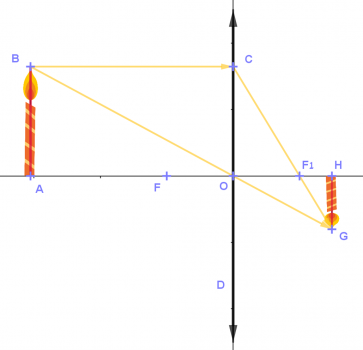
(המשך פתרון סעיף א)
\(\Downarrow\hspace{1cm}\)
\(OH=\Large\frac{2}{3}\normalsize+2=2\Large\frac{2}{3}\normalsize=מ"ס\space\Large\frac{8}{3}\)
\(\triangle {BAO}\sim\triangle{GHO}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OA}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(3=\Large\frac{OA}{(\Large\frac{8}{3})}\)
\(\Downarrow\hspace{1cm}\)
\(OA=מ"ס\space\space 8\)
\(\Large\frac{OA}{OF}\normalsize=\Large\frac{8}{2}\normalsize=4\)
סעיף ב
נתון כי: \(AB\perp AH\)
\(HG\perp AH\)
\(BC ∥ AH\)
\(OF=OF_1=מ"ס\space\space 2\)
\(\Large\frac{AB}{HG}\normalsize=0.5\)
יש לחשב את: \(\Large\frac{OA}{OF}\)
פתרון:
כנ"ל
נציב בפתרון של סעיף א.
\(\Large\frac{AB}{HG}\normalsize=0.5\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{2}{HF_1}\normalsize=0.5\)
\(HF_1=מ"ס\space\space 4\)
\(OH=4+2=מ"ס\space\space 6\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OA}{OH}\)
\(0.5=\Large\frac{OA}{6}\normalsize\)
\(OA=מ"ס\space\space 3\)
\(\Large\frac{OA}{OF}\normalsize=\Large\frac{3}{2}\)
סעיף ג
נתון כי: \(AB\perp AH\)
\(HG\perp AH\)
\(BC ∥ AH\)
\(OF=OF_1=מ"ס\space\space 2\)
\(\Large\frac{AB}{HG}\normalsize=1\)
יש לחשב את: \(\Large\frac{OA}{OF}\)
פתרון:
\(AB=CO=HG\)
במקרה זה המשולשים שהיו דומים הם חופפים.
\(\triangle{COF_1}\cong\triangle{GHF_1}\)
\(OF=OF_1=מ"ס\space\space 2\)
\(HO=מ"ס\space\space 4\)
\(\triangle{BAO}\cong\triangle{GHO}\)
\(AO=HO=מ"ס\space\space 4\)
\(\Large\frac{OA}{OF}\normalsize=\Large\frac{4}{2}\normalsize=2\)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
נתון כי: \(AB\perp AH\)
\(HG\perp AH\)
\(BC ∥ AH\)
\(OF_1=מ"ס\space\space 3\)
\(OH=מ"ס\space\space 5\)
יש לחשב את: \(\Large\frac{AB}{HG}\)
פתרון:
\(\triangle {COF_1}\sim\triangle{GHF_1}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{CO}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\)
מרובע ABCO הוא מלבן
(או חפיפת משולשים BCO ו- OAB)
\(\Downarrow\hspace{1cm}\)
\(CO=AB\)
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{3}{5-3}\normalsize=\Large\frac{3}{2}\)
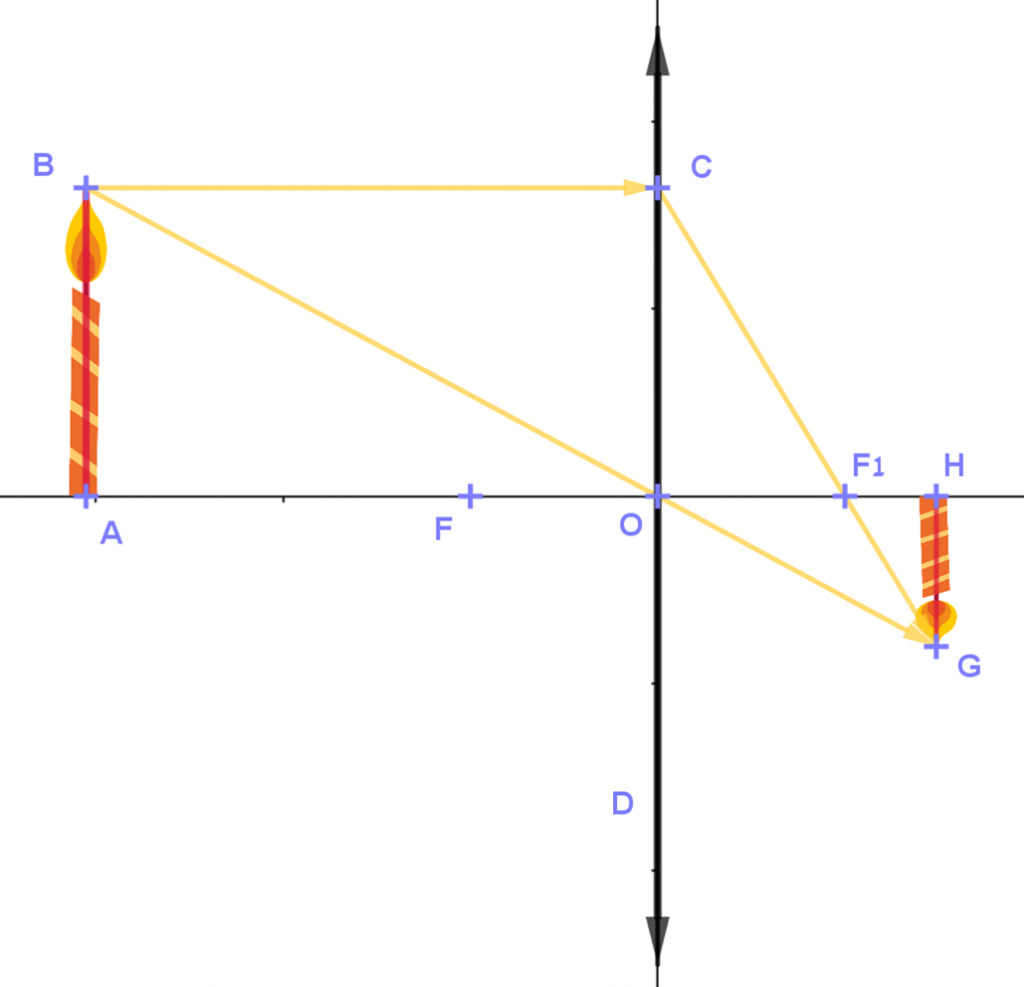
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
הסרטוט בבעיה שבמדרגה, זהה לזה שבבעיית המטרה. אך הבעיה במדרגה פשוטה יותר מבעיית המטרה ,כיוון שנידרש בה להוכיח דמיון בין זוג אחד של משולשים. בעוד שכדי לפתור את בעיית המטרה, יש להוכיח דמיון בין שני זוגות של משולשים.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
נתון כי: \(AB\perp AH\)
\(HG\perp AH\)
\(BC ∥ AH\)
\(AO=מ"ס\space\space 4\)
\(OH=מ"ס\space\space 6\)
יש לחשב את: \(\Large\frac{AB}{HG}\)
פתרון:
\(\triangle {BAO}\sim\triangle{GHO}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{OA}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{4}{6}\normalsize=\Large\frac{2}{3}\)
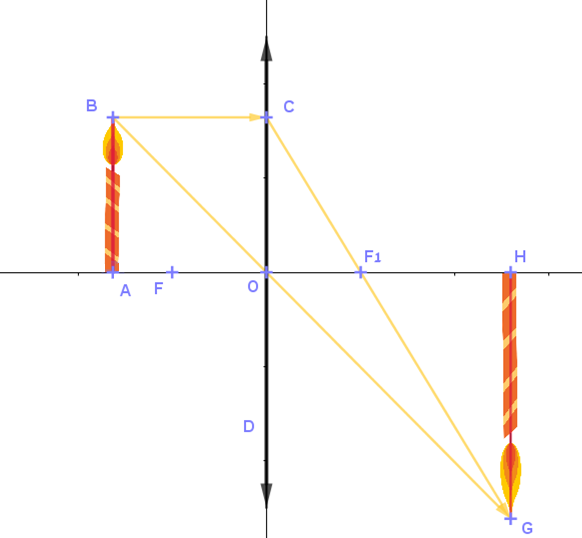
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
הסרטוט בבעיה שבמדרגה 2, זהה לזה שבבעיית מדרגה 1 ובבעיית המטרה. אך הבעיה במדרגה 2, פשוטה יותר מבעיית המטרה ומהבעיה במדרגה 1, כיוון שעל פי הנתונים בבעיה זו, ניתן לזהות באופן ישיר בין אילו משולשים יש להוכיח דמיון.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
הצעות לשאלות נוספות
- מדוע בתמונת האסטרונאוט וטיפת המים, הדמות המשתקפת דרך טיפת המים מוקטנת והפוכה?
- האם ישנם מצבים בהם לא נוצרת דמות אופטית של הנר? אם כן, באילו תנאים, ואם לא, מדוע?
- האם ניתן להכליל? באילו תנאים האורך של הדמות האופטית של הנר, גדול מאורך הנר? ובאילו תנאים האורך של הדמות האופטית של הנר, קטן מאורך הנר?באילו תנאים האורך של הדמות האופטית של הנר, שווה לאורך הנר?
- איך נראית דמות הנר כאשר \(0<AO<f\)?
תשובות לשאלות אלו ניתן להסיק מתוך התנסות ביישומון.
תשובה לשאלה 1: טיפת המים מתפקדת כעדשה מרכזת. דמות הפוכה ומוקטנת מתקבלת כשהעצם (האסטרונאוט) נמצא במרחק גדול יותר מ- \(2f\) ממרכז העדשה (טיפת המים).
באשכול דמיון בעדשות חלק ב – הכללה נענה על שאלות 2 ו- 3, ונגיע להכללות מפתיעות.
באשכול דמיון בעדשות חלק ג – זכוכית מגדלת נענה על שאלה 4.