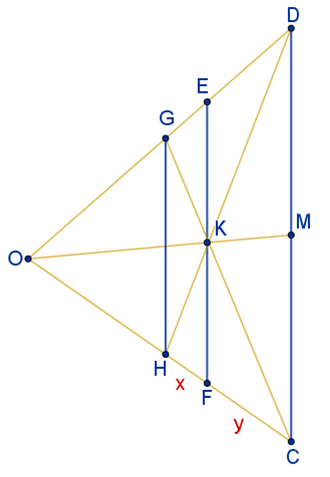
عنقود منظور – جزء ت – أعمدة إضاءة على أبعاد متساوية
2.3. درجة 3 لمسألة الهدف
أمامكم على اليسار تفسيرات الفنّان للرسم.
- ما هو نوع الشكل الرباعي CDEF الذي ينتج بين عمودي الإضاءة الأوليين، عندما يرسم الفنّان بمنظور أحدي نقطة الاختفاء؟
علّلوا.
- رسم الفنّان العمود الثالث بالاعتماد على الاعتبارات الهندسية وادعى أنه رسمه ملائم للواقع.
فيما يلي بعض الاعتبارات الهندسية التي عمل بها.
فسّرا الاعتبارات وأكملوا البرهان.
- إذا حللتم مسألة درجة 3، ارجعوا إلى مسألة الهدف.
يوجد في الرسم: HFFC=xy
يكون في الواقع: HF=FC ⟺ x=y
أردتُ أن أرسم العمود الثالث في مكان كهذا بحيث يتحقق:
إذا كان: x=y
فإن: CD=EF=GH
وجدت أن هذا يكون عندما يكون العمودي الثاني (أي EF) موجودًا في نقطة تقاطع قطري الشكل الرباعي HGDC
KEGH=KFGH=xx+y
EFGH=2yx+y
إذا كان: x=y
فإن: EFGH=1
⇓
EF=CD
أي أن الشكل الرباعي CDEF هو مستطيل،
وهذا ملائم للواقع!