אשכול דובי פנדה בגן החיות בווינה – למורה
הנחיות למורה
יחידה:
מתמטיקה
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
45-90 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (קונטקסט):
קריאת מפה, ביולוגיה, גאוגרפיה
ידע ומיומנויות מתמטיים נדרשים:
| נושאים | מושגים | מיומנויות |
|---|---|---|
| קנה מידה | – קנה מידה | – הבנת העיקרון של קנה המידה. – מציאת קנה המידה בהתאם לנתון לגבי אורך של משבצות בסרטוט. – מציאת השטח במציאות לפי השרטוט וקנה המידה שנמצא. |
| שטחים של מצולעים | – שטח | – הבנת המשמעות של מדידת שטח. – הבנת העקרון חישוב השטח: אם מרצפים צורה בעזרת צורות שאינן נחתכות, שטחה הוא סכום השטחים של הצורות המרצפות. |
| ישרים מקבילים וטרפז או שטח מלבן | – ישרים מקבילים – טרפז | – זיהוי טרפזים וחישוב שטח טרפז. – או לחילופין, חישוב השטח לפי שטחי מלבנים ושטחי משולשים. |
| יחס בין מספרים | – יחס כמנת שני גדלים | חישוב היחס בשאלה פי כמה גדל גודל אחד, לעומת הגודל השני. |
| שטח עיגול | – מרכז המעגל – רדיוס | – חישוב שטח עיגול – חישוב שטח גזרה – חיסור שטחים |
מטרות האשכול:
- פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך. הפתרון מוביל להעמקת ההבנה כיצד להיעזר בקנה מידה שבמפה לצורך חישוב שטחים במציאות, כמו גם למודעות לגבי התנאים שבהם נמצאים בעלי חיים (דובי פנדה) בגני חיות.
- פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות מתמטיים במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך. הפתרון מוביל לפיתוח ההבנה של הקשר הקיים בין זווית של גזרה לשטחהּ ולפיתוח הידע של חישוב שטח של גזרה.
ידע מתמטי ומיומנויות מתמטיים נלמדים (חדשים):
קנה מידה, שטחים של מצולעים, שטח גזרה.
מערך דידקטי מומלץ:
- רצוי להקדים ולשאול את התלמידים שאלות שתלמדנה על הידע שלהם לגבי קנה מידה לפני הצגת האשכול, למשל: באילו הקשרים מופיע קנה מידה? איך נעזרים בו? מה ההבדל בין קנה מידה שמופיע במפות המודפסות על נייר לבין מפות המופיעות במחשב?
כמו כן, גם ניתן לשאול את התלמידים מה ידוע להם על דובי פנדה? האם ראו במציאות דובי פנדה? אם כן, איפה? - בתחילת האשכול ישנה כתובת המפנה לקטע ווידאו המצולם בגן החיות בווינה. רצוי להציגו בכיתה. הקריינות בסרטון הווידאו היא בגרמנית; אפשר להשתיק את הקול.
ארגון הכיתה:
למידה בזוגות או בקבוצות.
ציוד נדרש:
מחשבון, מחשב כדי שניתן יהיה להפעיל את הישומונים (לא הכרחי).
ניהול השיעור:
המורה יאפשר לתלמידים לפתור את הבעיות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות וביישומונים. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי־הבנות.
המורה יבקש, מתלמידים שסיימו לפתור את הבעיות שבאשכול, להציע שאלה נוספת הקשורה לאשכול ולפתור אותה (בסוף הקובץ ישנה הצעה לבעיות נוספות שניתן לשאול).
דיון בכיתה:
- ניתן לקיים דיון קצר בכיתה לאחר פתרון בעיית מטרה 1. בדיון זה רצוי להתמקד בשאלה כיצד להיעזר בקנה המידה, כדי למצוא את השטח של גן החיות במציאות.
- דיון נוסף יש לקיים לאחר שהתלמידים פתרו את כל הבעיות שבאשכול. בדיון זה רצוי להתמקד בשאלה כיצד מוצאים שטח של גזרה.
- התלמידים יציגו ויסבירו את תשובותיהם בדיונים. רצוי לאפשר להם להציג דרכים שונות לפתרון.
- כמו כן יש לאפשר לתלמידים להציג את השאלות הנוספות שחשבו עליהן ולדון בפתרונות שהציעו.
- רצוי שהמורה יבחר, מבין שאלות התלמידים, את השאלות שלדעתו ראוי לדון בהן.
- אפשרות נוספת היא להציע לתלמידים להגיש את השאלות הנוספות ואת פתרונן כעבודת הגשה.
- אשכול זה יכול לעורר דיון בכתה על:
- הצורך בשמירה על בעלי חיים
- השאלה: באילו מצבים בעלי חיים נחשבים בעלי חיים בסכנת הכחדה.
- מהן הסיבות לכך שבעלי חיים נכחדים.
- תנאי החיים של בעלי חיים בגני חיות.
- השאלה: האם נכון ומוסרי לגדל בעלי חיים בגני חיות.
- ניתן לשלב דיון מסוג זה גם בשיעורי חינוך.
אשכול דובי פנדה בגן החיות בווינה
בכתובת הבאה קטע ווידאו שבו חוגגים יום הולדת 20 לדובת פנדה בשם Yang Yang בגן החיות בווינה.
קריינות הווידאו בגרמנית, תוכלו להשתיק את הקול.
https://www.youtube.com/watch?v=pi_Puzwf26c
(ניתן להפעיל כתוביות אוטומטיות בעברית, ע"י (1) הפעלת הסמל \(cc\) (2) בחירת השפה דרך סמל גלגל השיניים: (*) \(subtitles/CC\), (*) לחיצה על "<" (*) ואז באמצעות \(Auto-translate\) בחירה ב \(Hebrew\))
בואו נכיר את גן החיות בווינה, בירת אוסטריה.
גן חיות זה בנוי כחלק מפארק שנברון ונחשב לעתיק ביותר בעולם שעדיין פעיל ופתוח למבקרים.
גן החיות הוקם כמתחם מלכותי ב־31 ביולי 1752. מאז הקמתו הוא עבר שינויים רבים, אולם הוא עדיין פעיל במקום שבו הוקם. את גן החיות ייסד הקיסר פרנץ הראשון, אשר רצה להקים גן חיות מלכותי במושב הקיץ שלו.
בשנת 1980 הוחזקו בגן החיות כ־4,000 בעלי חיים ממינים שונים, אולם מאז המספר הצטמצם בשל המגמה לשפר את תנאי חייהן של החיות, וכיום מוחזקים בגן כ־2,500 בעלי חיים (ויקיפדיה).
לפניכם מפה של גן החיות (השטח הצהוב).
תמונה 1
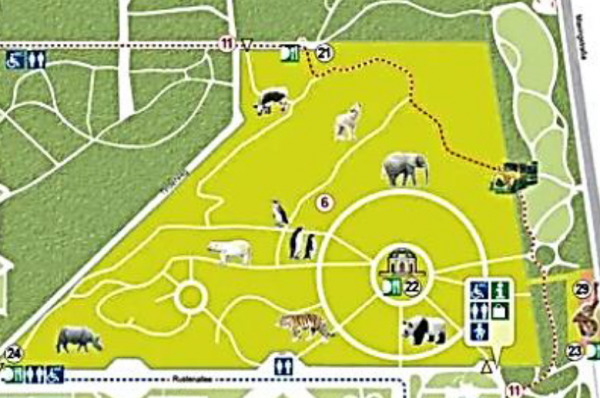
תמונות ואיורים מתוך אתר גן החיות: Tiergarten Schönbrunn
סקיצה 1 היא סרטוט סכמתי של גן החיות.
סקיצה 1
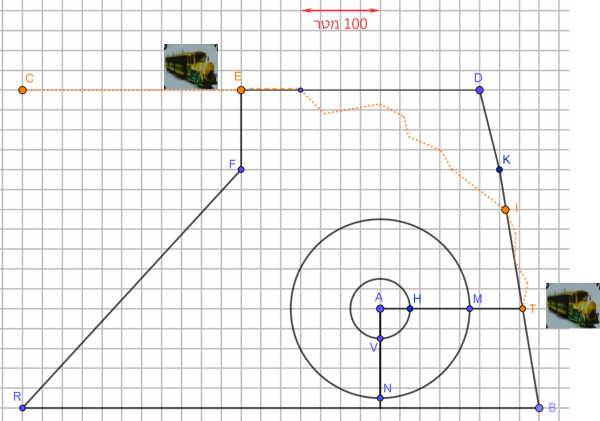
התבוננו בסקיצה 1 וענו על בעיית מטרה 1:
1. בעיית מטרה 1
בשטח גן החיות לא היו שינויים מאז המחצית השנייה של המאה 20.
אילו לכל בעל חיים היה מוקצה שטח שווה
- חשבו (בקירוב) מה היה השטח שהוקצה לכל בעל חיים בגן החיות בשנת 1980?
- חשבו (בקירוב) פי כמה גדל השטח המוקצה לכל בעל חיים כיום לעומת השטח שהוקצה בשנת 1980?
מצאו דרכים שונות לענות על השאלה.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- לסימון נקודות יש לבחור את
בסרגל הכלים, ואז לסמן את הנקודה על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. - לסרטוט קטע יש לבחור את
בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. - להגדרת מצולע וצביעתו
- יש לבחור את
בסרגל הכלים, ואז לסמן את קודקודי המצולע בזה אחר זה ובסיום לסמן שוב את הקדקוד הראשון, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. - לאחר הגדרת המצולע, ניתן לבחור צבע, מתוך הצבעים הנתונים מימין ביישומון, וללחוץ בתוך שטח המצולע הדרוש.
- יש לבחור את
- להגדלה/להקטנה של התצוגה, יש ללחוץ בעכבר על היישומון, ואז לגלגל את גלגלת העכבר כדי להגדיל/להקטין.
- לביטול הפעולה האחרונה יש לבחור את
בסרגל הכלים. - לניקוי הישומון כדי להתחיל מחדש, יש ללחוץ על חיצי האתחול
שבפינה הימנית העליונה.
פתרון לבעיית מטרה 1
קנה המידה הוא: אורך צלע של משבצת אחת מתאים ל־25 מטר במציאות.
- ניתן לחלק את שטח גן החיות לשני טרפזים ולמצוא את שטחם.
\(\space\)
\(\Large\frac{(12\cdot25+13\cdot25)\cdot4\cdot25}{2}+\frac{(13\cdot25+26\cdot25)\cdot12\cdot25}{2}\normalsize=ר"מ\space{177,500}\)מהחישוב מתקבל ששטח גן החיות הוא בקירוב 177,500 מ"ר.
אפשר לחשב את שטח הטרפזים שבסקיצה 1 ולהכפילו ב־25 בריבוע \((25^2)\)
אפשר לחלק את השטח למלבנים ולמשולשים.
\(\Large\frac{177,500}{4,000}\normalsize=ר"מ\space{44.375}\)
אילו לכל בעל חיים היה מוקצה שטח שווה אזי לכל אחד היה מוקצה (בקירוב) שטח של 44.375 מ"ר.
- \(\Large\frac{177,500}{2,500}\normalsize=ר"מ\space{71}\)
\(\Large\frac{71}{44.375}\normalsize=1.6\)
השטח גדל פי 1.6
דרך נוספת:
\(\Large\frac{4,000}{2,500}\normalsize=1.6\)
.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- לסימון נקודות יש לבחור את בסרגל הכלים, ואז לסמן את הנקודה על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- לסרטוט קטע יש לבחור את בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- למדידת אורך קטע יש לבחור את
בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. כתוצאה מכך, אורך הקטע יוצג. - להגדרת מצולע וצביעתו
- יש לבחור את בסרגל הכלים, ואז לסמן את קודקודי המצולע בזה אחר זה ובסיום לסמן שוב את הקדקוד הראשון, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- לאחר הגדרת המצולע, ניתן לבחור צבע, מתוך הצבעים הנתונים מימין ביישומון, וללחוץ בתוך שטח המצולע הדרוש.
- יש לבחור את
- להגדלה/להקטנה של התצוגה, יש ללחוץ בעכבר על היישומון, ואז לגלגל את גלגלת העכבר כדי להגדיל/להקטין.
- לביטול הפעולה האחרונה יש לבחור את בסרגל הכלים.
- לניקוי הישומון כדי להתחיל מחדש, יש ללחוץ על חיצי האתחול שבפינה הימנית העליונה.
הצעת פתרון למדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
שטח גן החיות 177,500 מ"ר (ראו פתרון בעיית מטרה 1).
מטרות מדרגה 1 של בעיית מטרה 1
- היישומון מאפשר לחלק את הסקיצה של גן החיות למצולעים שונים, ולמדוד אורכי קטעים, ובכך הוא מסייע לחשב את שטח גן החיות.
סקיצה 1
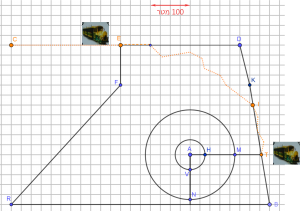
התבוננו בסקיצה 1 וחשבו מהו אורך החומה הדורשת חידוש במציאות.
פרטו חישוביכם.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- לסימון נקודות יש לבחור את בסרגל הכלים, ואז לסמן את הנקודה על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- לסרטוט קטע יש לבחור את בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- למדידת אורך קטע יש לבחור את בסרגל הכלים, ואז לסמן את שתי הנקודות שהן קצות הקטע, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט. כתוצאה מכך, אורך הקטע יוצג.
- להגדרת מצולע וצביעתו
- יש לבחור את בסרגל הכלים, ואז לסמן את קודקודי המצולע בזה אחר זה ובסיום לסמן שוב את הקדקוד הראשון, על-ידי לחיצה בעכבר במקום הדרוש בסרטוט.
- לאחר הגדרת המצולע, ניתן לבחור צבע, מתוך הצבעים הנתונים מימין ביישומון, וללחוץ בתוך שטח המצולע הדרוש.
- יש לבחור את
- להגדלה/להקטנה של התצוגה, יש ללחוץ בעכבר על היישומון, ואז לגלגל את גלגלת העכבר כדי להגדיל/להקטין.
- לביטול הפעולה האחרונה יש לבחור את בסרגל הכלים.
- לניקוי הישומון כדי להתחיל מחדש, יש ללחוץ על חיצי האתחול שבפינה הימנית העליונה.
הצעת פתרון למדרגה 2 של בעיית מטרה 1
אורך החומה BR: \(26\cdot25 = רטמ\space650\).מטרות מדרגה 2 של בעיית מטרה 1
- הבעיה דורשת להיעזר בקנה המידה ובסקיצה, כדי לחשב אורך של קטע במציאות. הבעיה פחות מורכבת מבעיית המטרה, ומאפשרת לתלמיד להבין כיצד להיעזר בקנה המידה לחישוב אורכי קטעים במציאות, ולחישוב שטח במציאות.
דובי פנדה חיים ברכסים ההרריים של סין.
דובי הפנדה הם בעלי חיים המצויים בסכנת הכחדה וקשה מאוד לגדלם בשבי. על פי הסקר שנערך ב־2014, מספר דובי הפנדה החיים בטבע הוא 1,864, ולהם נוסף מספר של מאות דובי פנדה החיים בשבי. זה אולי נשמע מעט, אך למעשה מדובר בסיפור הצלחה – אוכלוסיית דובי הפנדה כמעט והכפילה את עצמה משנות ה־70 של המאה הקודמת, אז נספרו 1,000 פרטים בטבע בלבד.
רק 49 דובי פנדה חיים כיום מחוץ לגבולות סין, ב־18 גני חיות המתפרשים על 13 מדינות בלבד.
אחד מגני החיות שבהם ישנם דובי פנדה הוא גן החיות בווינה.
דנה צפתה בדובי הפנדה שבגן החיות. היא קראה, שכדי לשרוד בטבע, כל דוב פנדה זקוק לסביבת מחייה של לפחות 10 קמ"ר.
דנה שאלה את המדריך בגן החיות: "השטח המוקצה כאן לכל דובי הפנדה קטן בהרבה מ־10 קמ"ר, כיצד זה שהם שורדים כאן?"
המדריך הסביר כי דוב פנדה ממוצע צורך כמות גדולה במיוחד של מזון:
12-38 ק"ג במבוק ביום! ולכן זקוק לשטח מחיה גדול. אך בשבי מספקים לו את האוכל למחייתו.
דנה שאלה: "מה שטח המחייה של דובי הפנדה כאן בגן החיות?"
המדריך ענה, כי אינו זוכר במדויק, אך השטח הוא בערך 1,500 מ"ר.
סקיצה 2
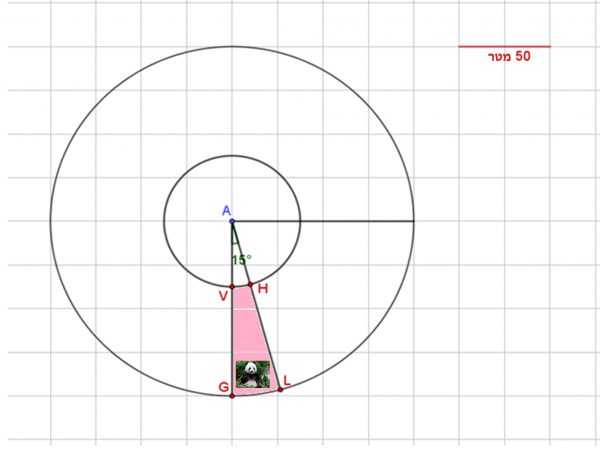
אזור המחייה של דובי הפנדה הוא האזור התחום על ידי הנקודות \(G\) , \(L\) , \(H\) , \(V\).
בדקו האם המדריך צדק בהערכתו? נמקו ופרטו את חישוביכם.
- אחרי שפתרתם את בעיית מטרה 2, המשיכו למה עוד ניתן לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון לבעיית מטרה 2
שטח אזור המחייה של דובי הפנדה בגן החיות הוא בקירוב:
\(\Large\frac{4^2\cdot\pi\cdot15\cdot25^2}{360}-\frac{1.5^2\cdot\pi\cdot15\cdot25^2}{360}=\frac{\pi\cdot15\cdot25^2}{360}\normalsize\cdot(4^2-1.5^2)=ר"מ\space{1,124.92}\)
הערכת המדריך, לגבי שטח המחייה, הייתה "גסה".
השטח קרוב יותר ל־1,000 מ"ר מאשר ל־1,500 מ"ר.
סקיצה 3
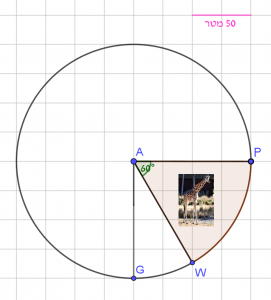
מצאו מה היחס בין שטח העיגול הגדול לבין שטח הגיזרה \(PAW\).
פרטו ונמקו חישוביכם.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 2.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- ניתן לגרור את נקודה \(W\) ולשנות את גודל הזווית בהתאם.
- ניתן להזין ערך לזווית \(\measuredangle{PAW}\)
- להגדלה/להקטנה של התצוגה, יש ללחוץ בעכבר על היישומון, ואז לגלגל את גלגלת העכבר כדי להגדיל/להקטין.
- לניקוי הישומון כדי להתחיל מחדש, יש ללחוץ על חיצי האתחול שבפינה הימנית העליונה.
הצעת פתרון למדרגה 1 של בעיית מטרה 2
בעיה 2.1.1
היחס בין שטח הגזרה \(PAW\) לשטח העיגול הוא: \(\Large\frac{60°}{360°}=\frac{1}{6}\).
מטרות מדרגה 1 של בעיית מטרה 2
- היישומון מאפשר לחקור ולהבין את הקשר הקיים בין זווית של גיזרה לבין שטח הגיזרה ושטח העיגול.
- הסקיצה של הבעיה במדרגה 1 פחות מורכבת מזו שבבעיית המטרה 2. לכן, הבעיה הזו בשילוב היישומון מאפשרים להבין כיצד למצוא שטח גיזרה על פי הזווית שלה ועל פי רדיוס המעגל.
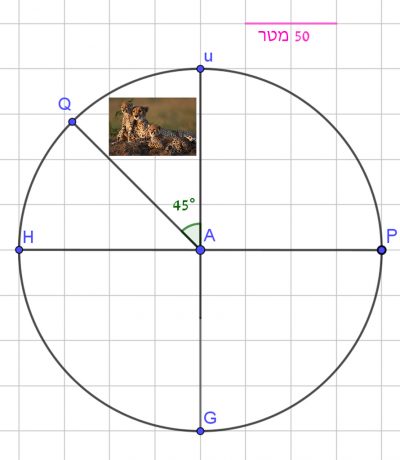
הצ'יטה (ברדלס) שבגן החיות נמצאת בשטח הגיזרה \(QAU\).
התבוננו בסקיצה 4 (\(A\) מרכז המעגל) ומצאו מה היחס בין שטח העיגול הגדול לבין שטח הגזרה \(QAU\).
פרטו ונמקו חישוביכם.
סקיצה 4
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 2.
הצעת פתרון למדרגה 2 של בעיית מטרה 2
בעיה 2.2.1
היחס בין שטח הגזרה \(QAU\) לשטח העיגול הוא: \(\Large\frac{45°}{360°}=\frac{1}{8}\).
מטרות מדרגה 2 של בעיית מטרה 2
- הסקיצה של הבעיה במדרגה זו פחות מורכבת מזו שבמדרגה 1 ומאפשרת לזהות ששטחה של גיזרה, שהזווית שלה בת 45 מעלות, הוא שמינית מכל שטח העיגול; באופן זה ניתן להגיע להבנה כיצד למצוא שטח גיזרה על פי הזווית שלה ועל פי רדיוס המעגל.
הצעות לשאלות: מה עוד אפשר לשאול?
לפניכם הצעות לבעיות נוספות אותן ניתן להציע לתלמידים שסיימו לפתור את הבעיות שבאשכול, כשיעורי בית או כעבודת הגשה:
שאלה 1
באשכול נתון כי:
רק 49 דובי פנדה חיים כיום מחוץ לגבולות סין, ב־18 גני חיות המתפרשים על 13 מדינות בלבד.
אילו טענות מבין הטענות הבאות נכונות:
- מבין 18 גני החיות, שהוזכרו לעיל, יימצא גן חיות אחד שחיות בו לפחות 4 פנדות.
- מבין 13 מדינות, שהוזכרו לעיל, תימצא מדינה אחת שחיות בה לפחות 4 פנדות.
- מבין 13 מדינות, שהוזכרו לעיל, יכולה להימצא מדינה אחת שיש בה 7 גני חיות שבהם יש פנדות.
הסבירו תשובתכם.
שאלה 2
במקרה שיש צורך להגדיל פי 2 את שטח המחייה של דובי הפנדה, מה יש לעשות לשם כך?
בחרו את התשובה הנכונה/התשובות הנכונות, ונמקו תשובתכם:
- להגדיל את הרדיוס \(AG\) פי 2
- להגדיל כל אחד מהרדיוסים \(AG\) ו־\(AV\) פי 2
- להגדיל את זווית \(\measuredangle{GAL}\) פי 2
- להגדיל כל אחד מהרדיוסים \(AG\) ו־\(AV\) פי 1.4