عنقود تشابه في عدسات – جزء ب – تعميم
تعلمنا في العنقود السابق “تشابه في عدسات – جزء أ“:
- ما هي عدسة مُحدبة
- عن بؤرتي العدسة المحدبة (F,F1),
وعن بُعد البؤرتين عن مركز العدسة: OF=OF1=f - عن مسار أشعة الضوء التي تمر خلال عدسة محدبة
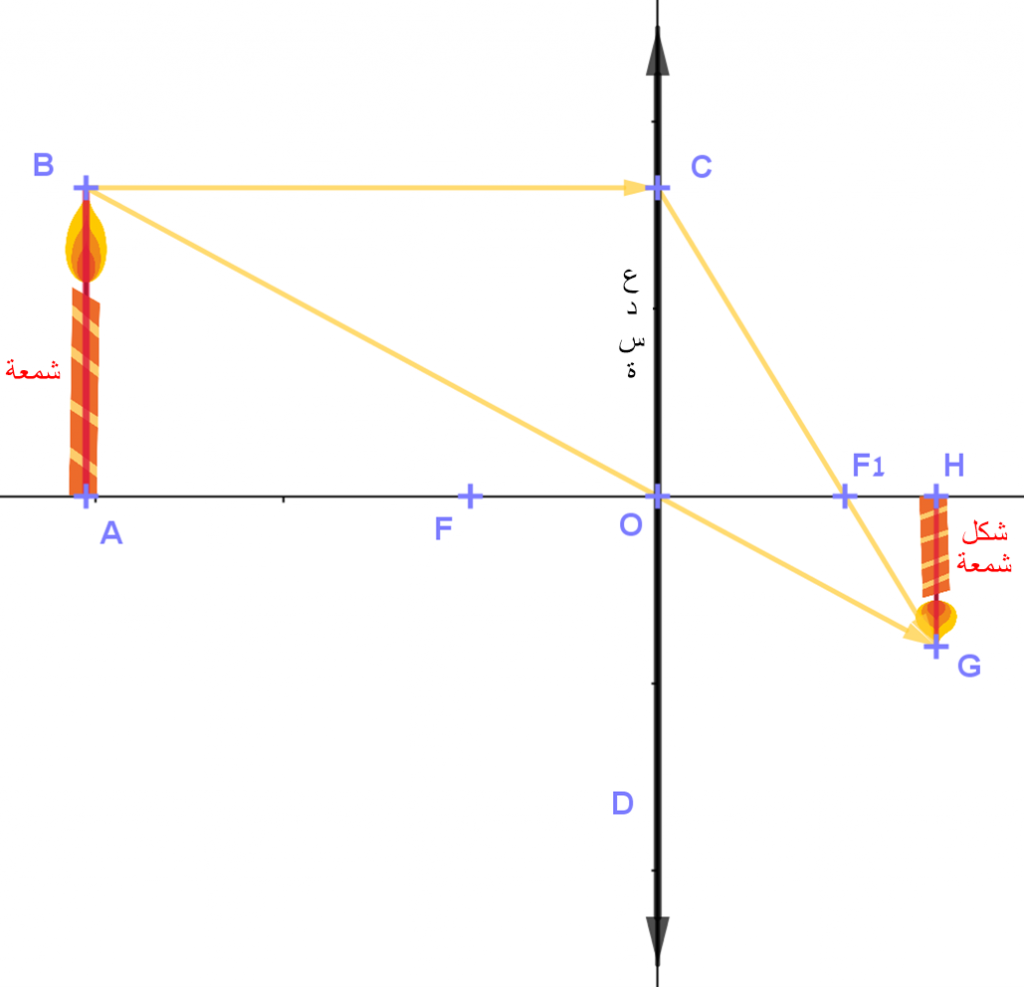
- عن رسم شكل بصري (أوبتي) لشمعة (HG) التي تنعكس في عدسة محدبة (انظروا الرسم المرفق)
- الشكل البصري عندما AO>f, هي حقيقية ومعكوسة.
يمكن أن يكون كِبرها أصغر من كِبَر الشمعة، أكبر أو مساوٍ لها.
نفحص في هذا العنقود بماذا يتعلق كِبَر الشكل البصري، عندما يكون AO>f.
1. مسألة هدف 1 – تعميم
برهنا في عنقود “تشابه في عدسات – جزء أ“، أنه عندما يكون AO>f, يكون:
ABHG=COHG=OF1HF1
ABHG=AOOH
- استعينوا بالحقائق التي برهنتها وأكملوا الجدول، عللوا إجاباتكم.
يمكنكم الاستعانة بالتطبيق المرفق.
بُعد البؤرة عن مركز العدسة f بُعد الشمعة عن مركز العدسة AO بُعد الشكل عن مركز العدسة HO AOf=k النسبة بين كِبَر الشمعة وبين كِبر شكل الشمعة ABHG 2 سم 8 سم 8/3 سم 4 3 2 سم 6 سم احسبوا احسبوا احسبوا 2 سم 4 سم 4 سم 2 1 2 سم 3 سم 6 سم 1.5 0.5 2 سم 2.5 سم احسبوا احسبوا احسبوا تعميم f AO ———— أكملوا أكملوا - استنتجوا استنتاجات من الجدول، عندما يكون AO>f:
- بالنسبة لأي قيم k (AOf=k)، يكون طول الشمعة أكبر من طول شكل الشمعة؟
- بالنسبة لأي قيم k (AOf=k)، يكون طول الشمعة مساويًا لطول شكل الشمعة؟
- بالنسبة لأي قيم k (AOf=k)، يكون طول الشمعة أكبر من طول شكل الشمعة؟
عللوا إجاباتكم.
يمكنكم الاستعانة بالتطبيق المرفق.
- ماذا يمكن أن نستنتج بالنسبة لشكل الشمعة عندما k=1؟
ارسموا رسمًا ملائمًا، وبرهنوا جوابكم بطريقة هندسية.
يمكنكم الاستعانة بالتطبيق المرفق.
- إذا حليّتم مسألة هدف 1، انتقلوا إلى ماذا يمكن أن نسأل أيضًا.
- أو حلوا، حسب الحاجة، مسألة درجة 1.
- يمكن تغيير مكان الشمعة بواسطة جرّ النقطة A الى اليمين وإلى اليسار.
- يمكن تغيير ارتفاع الشمعة بواسطة جرّ النقطة B الى الأعلى والى الاسفل.
- يمكن تعيين مثلثات مختلفة بواسطة اختيار لون المثلث في القائمة، واختيار 3 رؤوس.












