אשכול מדידת טמפרטורה בסולמות שונים - למורה
יישומונים
- – – – – –
הנחיות למורה
יחידה:
מדעים
כיתה מומלצת:
כיתה ח / כיתה ט
משך הזמן המומלץ:
45-90 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
- סולמות מדידה של טמפרטורה (צלזיוס, פרנהייט, קלווין) טמפרטורת האפס המוחלט – פיזיקה.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| פונקציה קווית | – פונקציה קווית היא פונקציה שבה קצב ההשתנות הוא אחיד. – טבלת ערכים – קצב השתנות אחיד – שיפוע הקו הישר – ייצוג אלגברי של הפונקציה הקווית | – האחדה בין שלושה היבטים של הפונקציה הקווית: פונקציה שבה קצב ההשתנות הוא אחיד, פונקציה שהגרף שלה הוא קו ישר, ופונקציה שהייצוג האלגברי שלה הוא מהצורה: y=mx+b. – מציאת ייצוג אלגברי של פונקציה קווית בהינתן ערכיה בשתי נקודות. |
| ייצוג תופעות באמצעות פונקציה קווית | – טבלת ערכים – קצב השתנות אחיד – שיפוע הקו הישר – ייצוג אלגברי של הפונקציה הקווית | – פתירת בעיות המתארות תהליכי השתנות באמצעות פונקציה קווית. |
| משתנים, ביטויים אלגבריים והכללה של תופעות מספריות | – ביטוי אלגברי – משתנה | – מעבר מייצוג מספרי (באמצעות תמונות של מדי-חום שונים) לביטוי אלגברי. |
| בעיות אורייניות מתוך מציאות הקרובה לתלמידים | – טמפרטורה – מעלות צלזיוס – מעלות פרנהייט – מעלות קלווין – טמפרטורת האפס המוחלט – קצב השתנות אחיד – שיפוע הקו הישר – פונקציה קווית | – פתרון בעיות המשלבות בין הבנת טקסט מילולי והצגת נתונים הלקוחים מתוך המציאות, לביצוע החישובים המתאימים לפתרון הבעיות. – קריאת נתונים מתוך תמונות של מדי-חום שונים |
מטרות האשכול:
- הכרה של סולמות שונים למדידת טמפרטורה.
- פיתוח המיומנות של מעבר בין סולמות המדידה השונים של הטמפרטורה.
- הכרה של המושג "האפס המוחלט"
- פיתוח ההבנה שקיים קשר לינארי בין מעלות צלזיוס למעלות פרנהייט, בין מעלות צלזיוס ומעלות קלווין ובין מעלות קלווין למעלות פרנהייט
- פיתוח ההבחנה בהבדלים ובדמיון הקיימים בין הגרף המתאר המרה ממעלות צלזיוס לפרנהייט לבין הגרף ההפוך המתאר המרה ממעלות פרנהייט למעלות צלזיוס.
- העמקה בנושא פונקציה קווית
מערך דידקטי מומלץ:
ארגון הכיתה:
למידה בזוגות או בקבוצות.
שאלות מומלצות לדיון כיתתי
רצוי להקדים ולשאול את התלמידים שאלות שתלמדנה על הידע שלהם לגבי מדידת טמפרטורה לפני הצגת האשכול, כמו: לצורך מה מודדים טמפרטורה? אילו סולמות למדידת טמפרטורה הם מכירים? אילו סוגים של מדי-חום הם מכירים?
ניתן לקיים דיון קצר בכיתה לאחר בעיית מטרה 1 סעיף א ודיון נוסף לאחר שהתלמידים ענו גם על סעיפים ב ו- ג. בדיונים אלו התלמידים יציגו ויסבירו את תשובותיהם. רצוי לעודד אותם להציג דרכים שונות לפתרון.
לסיכום הדיון התלמידים יציגו את השאלות הנוספות שחשבו עליהן ואת הפתרונות לשאלות אלה.
ניתן לבקש מהתלמידים לחפש באינטרנט מידע לגבי האנשים שעל שמם נקראים הסולמות השונים למדידת טמפרטורה וכן לחפש הסברים לפי אילו עקרונות נקבעו הסולמות השונים.
אשכול מדידת טמפרטורה בסולמות שונים
תיאור סיטואציה
בישראל נהוג למדוד טמפרטורה במעלות צלזיוס ∘C.
בארה"ב נהוג למדוד טמפרטורה במעלות פרנהייט ∘F.
במדע נהוג למדוד טמפרטורה במעלות קלווין ∘K.
לפניכם מדי טמפרטורה (מדי-חום) מסוגים שונים.
בתמונה 1 מד-חום העמיד במים ומודד טמפרטורה במעלות צלזיוס (C) ובמעלות פרנהייט (F).
בתמונה 2 מופיעים שני מדי-חום: האחד מודד טמפרטורה במעלות צלזיוס (C) והשני במעלות פרנהייט (F)
ובתמונה 3 מופיע מד-חום המודד טמפרטורה במעלות צלזיוס (C) ובמעלות קלווין (K).
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
1. בעיית מטרה 1
האפס המוחלט שווה ל-0∘K. האפס המוחלט הוא הטמפרטורה הנמוכה ביותר. לא ניתן להביא חומר לאפס המוחלט, אך ניתן לשאוף אליו. את הטמפרטורה הנמוכה ביותר הצליח למדוד החוקר הבריטי וויליאם תומפסון הידוע כלורד קלווין בשנת 1848.
התבוננו בתמונות של מדי הטמפרטורה (מדי-החום) השונים וענו על השאלות הבאות:
- מצאו לכמה מעלות שווה האפס המוחלט במעלות צלזיוס? במעלות פרנהייט? פרטו חישוביכם.
- מצאו ביטוי לפונקציית המרה ממעלות קלווין למעלות פרנהייט. פרטו חישוביכם.
- האם תיתכן טמפרטורה של −400∘F? ושל −500∘F? הסבירו תשובתכם.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לשאלת ההמשך.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
פתרון בעיית מטרה 1
פתרון בעיית מטרה 1 סעיף א
מתמונה 2 ניתן להסיק כי הקשר בין מעלות צלזיוס ומעלות פרנהייט הוא לינארי. עליה ב- 10∘C מתאימה לעליה ב- 18∘F. לכן, שיפוע הפונקציה הלינארית הוא 1.8, ונוסחת ההמרה ממעלות צלזיוס למעלות פרנהייט היא yF=1.8xC+32 (בתמונה 1 בולט ש- −40∘C=−40∘F).
מתמונה 3 ניתן להסיק כי הקשר בין מעלות צלזיוס ומעלות קלווין הוא לינארי. עליה ב- 10∘C מתאימה לעליה ב- 10∘K, לכן שיפוע הפונקציה הלינארית הוא 1. נוסחת ההמרה ממעלות צלזיוס למעלות קלווין היא yK=xC+273. על ידי הצבה בנוסחאות ההמרה מתקבלות התשובות הבאות:
−273∘C=0∘K , −273∘C=−459.4∘F
ולכן: 0∘K=−459.4∘F
פתרון בעיית מטרה 1 סעיף ב
דרך א'
בניית טבלת ערכים משותפת. לדוגמא:
| טמפרטורה ב- ∘C | טמפרטורה ב- ∘K | טמפרטורה ב- ∘F |
|---|---|---|
| 0∘C | 273∘K | 32∘F |
| 10∘C | 283∘K | 50∘F |
| 20∘C | 293∘K | 68∘F |
| 30∘C | 303∘K | 86∘F |
ניתן להסיק שהקשר בין מעלות קלווין למעלות פרנהייט הוא קשר לינארי.
כאשר הטמפרטורה עולה ב- 10∘K הטמפרטורה עולה ב- 18∘F. לכן שיפוע הפונקציה הקווית הוא 1.8, ופונקציית ההמרה (או נוסחת ההמרה) מקלווין לפרנהייט היא: yF=1.8xK−459.4.
דרך ב'
על פי הנוסחאות שנמצאו בבעיית מטרה 1 סעיף א:
yK−273=xC , yF=1.8(yK−273)+32
לכן: yF=1.8yK−459.4
כלומר: yF=1.8xK−459.4 (החלפת המשתנה yK ב- xK)
פתרון בעיית מטרה 1 סעיף ג
טמפרטורה של −400∘F אפשרית כי במעלות קלווין הטמפרטורה היא חיובית: 33∘K.
טמפרטורה של −500∘F לא אפשרית כי במעלות קלווין הטמפרטורה היא שלילית: −22.56∘K ובמעלות קלווין לא תתכן טמפרטורה שלילית.
1.1 מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
התבוננו בתמונות של מדי-החום ובארבעת הגרפים הנתונים.
כתבו איזה גרף, מבין ארבעת הגרפים הנתונים ביישומון, מבטא:
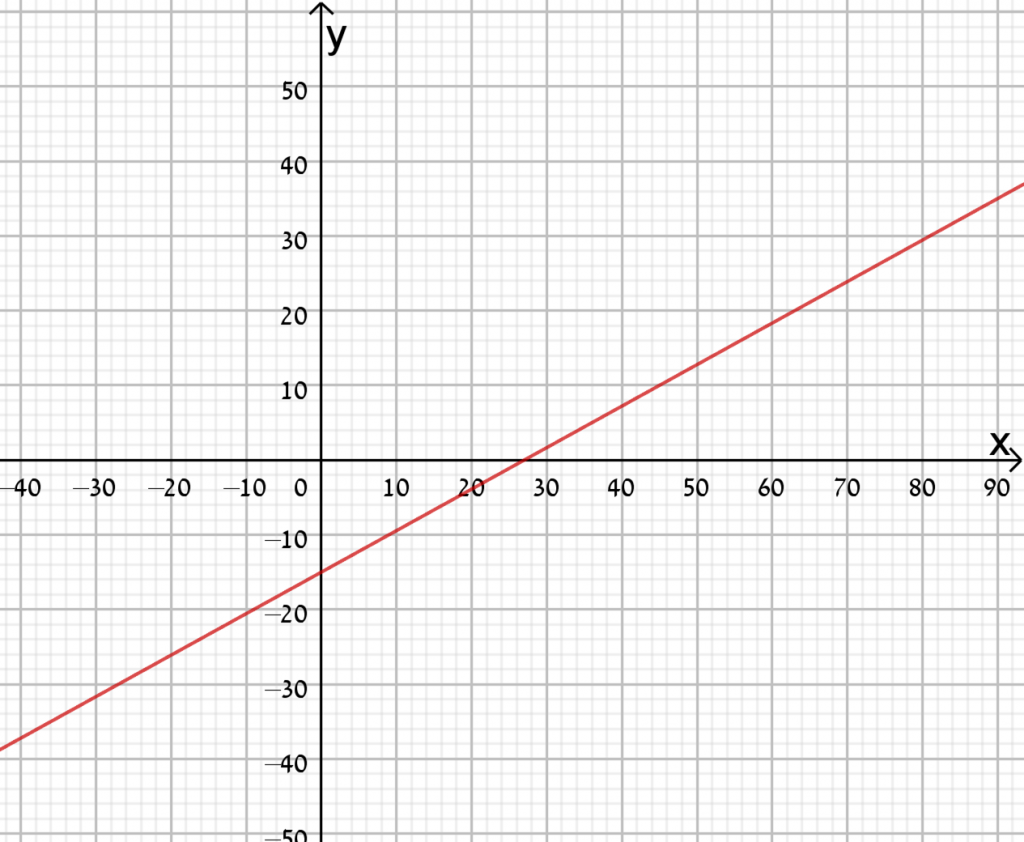
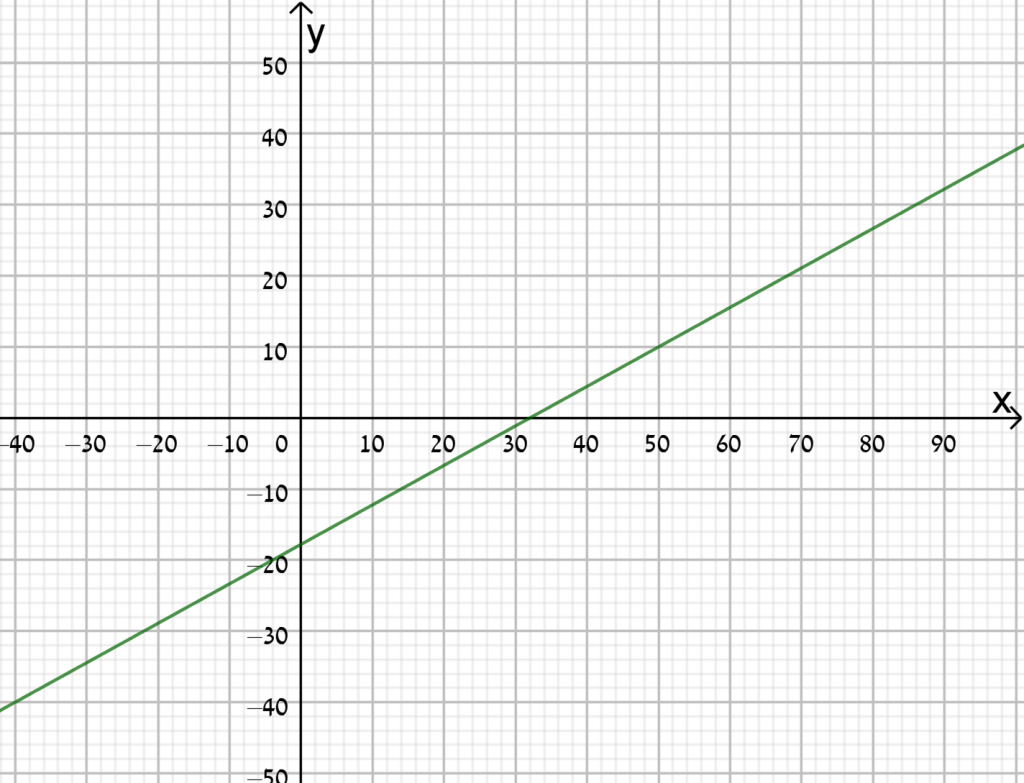
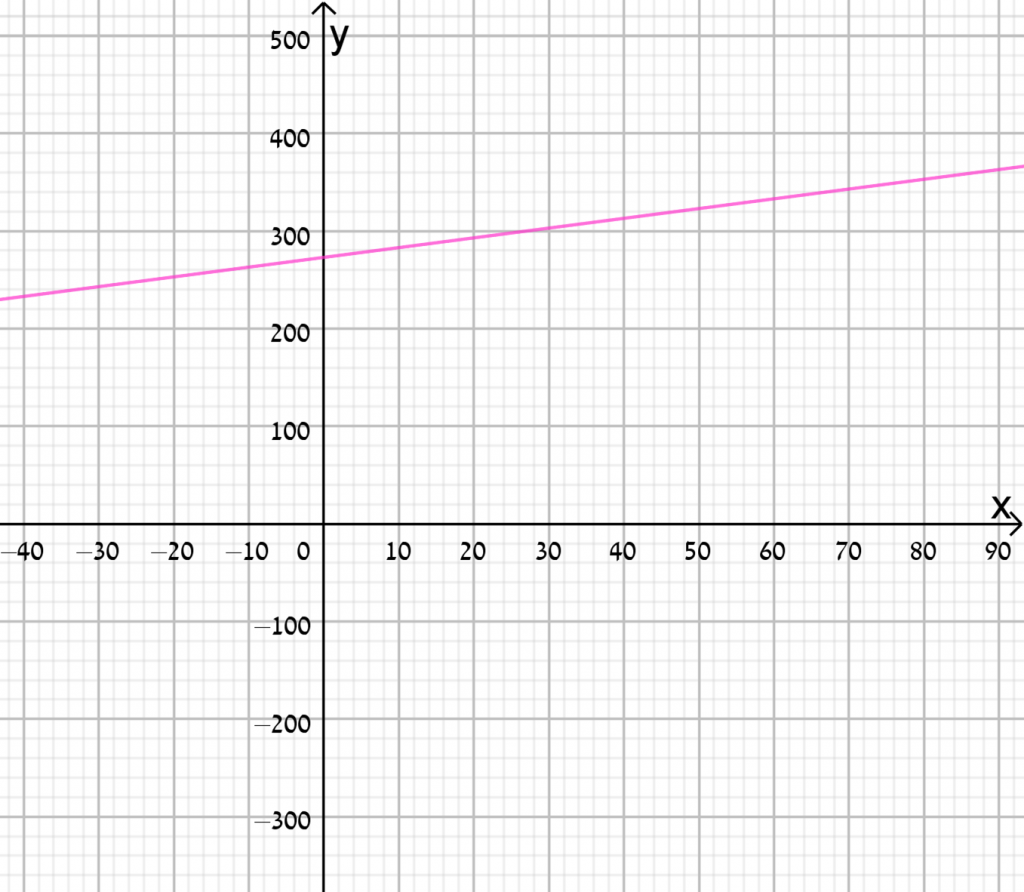
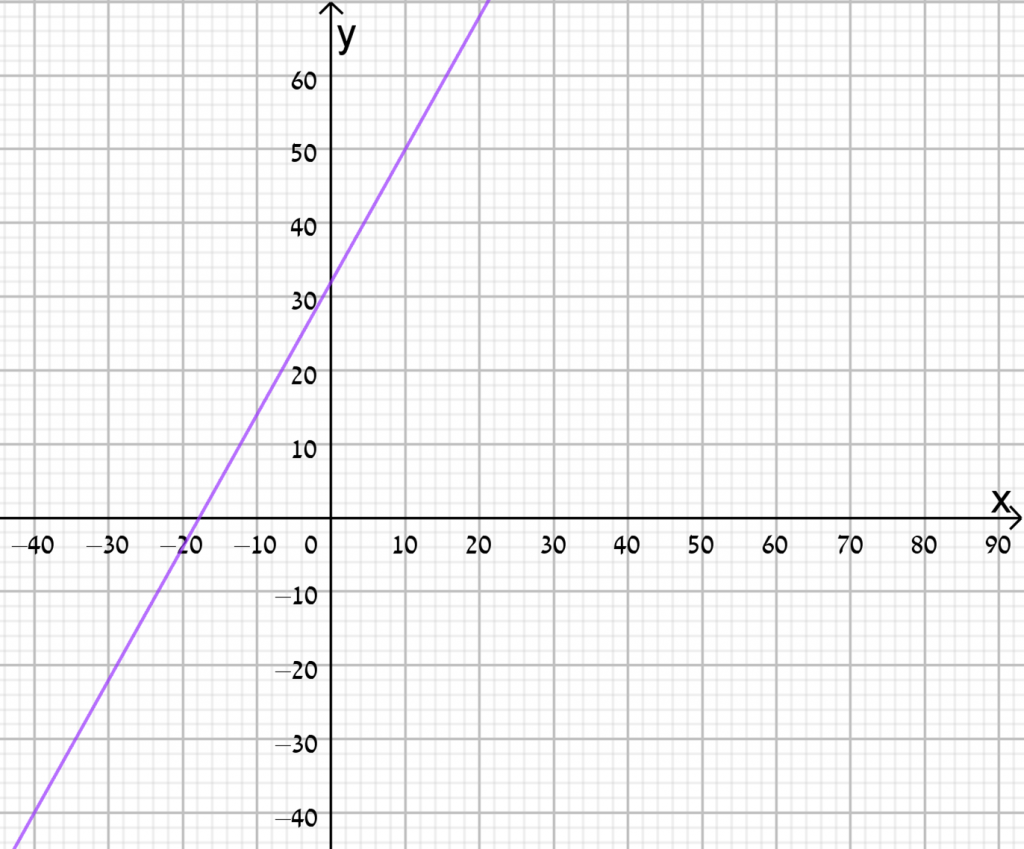
- המרה ממעלות צלזיוס למעלות פרנהייט
- המרה ממעלות פרנהייט למעלות צלזיוס
- המרה ממעלות צלזיוס למעלות קלווין
- המרה ממעלות קלווין למעלות צלזיוס
נמקו תשובתכם.
הערה: לא לכל הסעיפים למעלה ישנו גרף מתאים.
תוכלו להיעזר ביישומון המופיע למטה.
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
(ניתן ללחוץ על כל אחד מגרפים הבאים ולהגדילם במידת הצורך)
- הציגו את הגרף המבוקש (א, ב, ג או ד)
- רשמו שיעורי נקודות ובדקו אם הן מופיעות על הגרף:
הנקודה תִּצָבַּע בירוק אם היא מתאימה, ובאדום אם איננה מתאימה.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
גרף ב מתאים לפונקציית המרה ממעלות פרנהייט למעלות צלזיוס.
גרף ג מתאים לפונקציית המרה ממעלות צלזיוס למעלות קלווין.
גרף ד מתאים לפונקציית המרה ממעלות צלזיוס למעלות פרנהייט.
מטרת מדרגה 1 לבעיית מטרה 1
בעזרת הגרפים ניתן להבין שקיים קשר לינארי בין מעלות צלזיוס למעלות פרנהייט, וכן בין מעלות צלזיוס ומעלות קלווין, ולכן ניתן למצוא את נוסחאות ההמרה בעזרת הידע למציאת ביטוי לפונקציה קווית על פי שתי נקודות שעל הקו הישר.
בעזרת נוסחאות ההמרה ניתן למצוא לכמה מעלות צלזיוס ולכמה מעלות פרנהייט שווה האפס המוחלט.
לבעיה מצורף יישומון בעזרתו ניתן לבדוק אילו נקודות נמצאות על איזה גרף.
1.2 מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
התבוננו בתמונות של מדי-החום וענו:
- לכמה מעלות פרנהייט שווה טמפרטורה של 0∘C?
- לכמה מעלות פרנהייט שווה טמפרטורה של 140∘C?
בעיה 1.2.2
התבוננו בתמונות של מדי-החום וענו:
- אם הטמפרטורה עולה ב- 10∘K בכמה מעלות צלזיוס תעלה הטמפרטורה? פרטו חישוביכם.
- אם הטמפרטורה עולה ב- 10∘K בכמה מעלות פרנהייט תעלה הטמפרטורה? פרטו חישוביכם.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 3.
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
- טמפרטורה של 0∘C שווה ל- 32∘F.
- טמפרטורה של 140∘C שווה ל- 284∘F.
על פי גרף ד: ביטוי לפונקציית ההמרה ממעלות צלזיוס למעלות פרנהייט: y=1.8x+32
1.8⋅140+32=284
בדרך אחרת: (על פי תמונת מד-חום 2 הנתונה): 212+18⋅140−10010=284
בעיה 1.2.2
עליית טמפרטורה ב- 10∘K שווה לעליה ב- 10∘C (תמונה 3), עליית טמפרטורה ב- 10∘C שווה לעלייה ב- 18∘F (תמונה 2) ומכאן עליית טמפרטורה ב- 10∘K שווה לעליית טמפרטורה ב- 18∘F.
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
מטרת המדרגה למקד את תשומת הלב לנקודה (0,32), שניתן לזהותה בתמונה של מד-חום 2 הנתון. בעזרת הנקודה הזו ניתן לזהות את הגרף של פונקציית ההמרה מצלזיוס לפרנהייט, ובעזרת הגרף ניתן לחשב את הביטוי של פונקציית ההמרה מצלזיוס לפרנהייט ולמצוא לכמה מעלות פרנהייט שוות 140∘C.
בדרך אחרת: ניתן לחשב לכמה מעלות פרנהייט שוות 140∘C, בעזרת זה שמבחינים במד-החום המתאים, בתמונה 2 המצורפת, שעלייה ב- 10∘C שווה לעלייה ב- 18∘F.
בעיה 1.2.2
פתרון השאלה במדרגה מבהיר כי ההשתנות של פונקציית ההמרה ממעלות קלווין למעלות פרנהייט היא השתנות קבועה, ולכן זו פונקציה קווית, ואפשר למצוא את שיפוע הפונקציה הקווית הזו.
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית מטרה 1.
- לפניכם גרף שממיר ערכים ממעלות צלזיוס לפרנהייט וגרף נוסף שממיר ערכים ממעלות צלזיוס לקלווין.
- היעזרו בגרפים המוצגים כדי למלא ערכים בטבלה.
דוגמה לפתרון מדרגה 3 לבעיית מטרה 1
השלמת הטבלה:
| טמפרטורה ב- ∘C | טמפרטורה ב- ∘K | טמפרטורה ב- ∘F |
|---|---|---|
| 0∘C | 273∘K | 32∘F |
| 10∘C | 283∘K | 50∘F |
| 20∘C | 293∘K | 68∘F |
מטרת מדרגה 3 לבעיית מטרה 1
לעזור לתלמיד לארגן את הנתונים בטבלת ערכים בצורה כזו שתאפשר לו למצוא את הקשר הקיים בין מעלות קלווין למעלות פרנהייט.
לבעיה מצורפים יישומונים בעזרתם ניתן למלא את הטבלה ולבדוק את התשובות לבעיה.
ניתן ללחוץ על כל אחת מהתמונות ולהגדיל אותה במידת הצורך
הצעות לשאלות נוספות
בעיה 1
רועי, שגר בחיפה, התקשר לחברו שגר בבוסטון שבארה"ב.
חברו סיפר לו שאצלם יורד שלג וקר מאוד, הטמפרטורה היא 14∘F.
רועי סיפר שבחיפה קר, אבל לא נורא, הטמפרטורה היא 15∘C.
חשבו מה היה הפרש הטמפרטורות בין זו שבחיפה לבין זו שבבוסטון. פרטו חישוביכם.
בעיה 2
נקודת הקיפאון של המים במעלות צלזיוס היא 0∘C ונקודת הרתיחה של המים היא 100∘C. ההפרש ביניהן הוא 100∘C.
חשבו מהו ההפרש בין נקודת הרתיחה של המים לבין נקודת הקיפאון של המים במעלות פרנהייט ובמעלות קלווין. נמקו תשובתכם.
בעיה 3
- האם ייתכן שהטמפרטורה במעלות צלזיוס ובמעלות פרנהייט תהיה שווה? נמקו תשובתכם בדרכים שונות.
- האם ייתכן שכאשר הטמפרטורה במעלות צלזיוס היא שלילית, אז הטמפרטורה במעלות פרנהייט היא חיובית? נמקו תשובתכם בדרכים שונות.
מקורות מידע
האפס המוחלט: מכון דוידסון