אשכול מס הכנסה ג – קשר בין מס הכנסה ומשכורת אחרי מס – למורה
הנחיות למורה
אשכול מס' 3 מתוך 4 אשכולות.
חשוב לבצע אשכול זה אחרי אשכול א' – "כיצד לחשב מס הכנסה ומשכורת לאחר ניכוי מס הכנסה", שבו התלמידים חישבו מס הכנסה ושכר של עובדים אחרי ניכוי מס הכנסה. ואחרי אשכול ב' – "מס הכנסה בייצוגים שונים", שבו חישבו את הסכום שינוכה ממשכורת כלשהי עבור מס הכנסה באופן כללי, בעזרת ייצוגים שונים של פונקציה.
באשכול זה יימצאו קשרים בין הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין תשלום מס ההכנסה, לבין הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין המשכורת לאחר ניכוי מס ההכנסה.
יחידה:
חינוך פיננסי וכלכלה
כיתה מומלצת:
כיתה ט / כיתה י
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (קונטקסט):
- הבנת שיטת המיסוי הנהוגה בישראל תוך שימוש במידע מקורי.
- יכולת לעבור בין ייצוגים שונים של מידע.
- קריאת מידע והסקת מסקנות אופרטיביות ממנו, משכורת ברוטו, מס הכנסה, מס הכנסה מצטבר, משמעות של מדרגות מס הכנסה.
- קשרים בין ניכוי עבור מס הכנסה לבין משכורת אחרי ניכוי זה.
ידע ומיומנויות מתמטיים נדרשים:
| נושאים | מושגים | מיומנויות |
|---|---|---|
| קריאת גרפים | גרף של פונקציה | |
| הדגמת תופעות בעזרת גרף | ||
| אחוזים: תמורת האחוז, מציאת הערך השלם | מושג האחוז | חישוב אחוזים |
| משתנים וביטויים אלגבריים | משתנה ביטוי אלגברי | בניית ביטוי אלגברי לתשלום מס הכנסה במדרגות שונות זיהוי ביטוי אלגברי לתשלום מס הכנסה במדרגות שונות |
| שאלות מילוליות המשלבות אחוזים | יכולת ניתוח מצבים מחיי היום יום באמצעות כלים מתמטיים מעבר בין ייצוגים שונים של מידע (מילולי, אלגברי, גרפי, טבלה) |
|
| מערכת צירים | מערכת צירים טבלת ערכים | הצבת שיעורי נקודות |
| סימון נקודות וקריאת נקודות במערכת צירים | שיעורי נקודות | מיומנות של קריאת גרפים: מציאת ערך y כשנתון ערך x ומציאת ערך x כשנתון ערך y |
| ייצוגים שונים של פונקציה | פונקציה תיאור מילולי של פונקציה | קישור בין ייצוגים שונים של פונקציה קווית קריאת מידע מגרף מעבר בין ייצוגים שונים של פונקציה |
| תכונות של פונקציה | פונקציה קווית בייצוגים שונים ותכונותיה פונקציה קווית למקוטעין | זיהוי עליה וירידה של פונקציה |
| השתנות של פונקציה: עליה וירידה, קצב שינוי, קצב שינוי אחיד, שיפוע של פונקציה | קצב שינוי שיפוע | זיהוי וחישוב קצב שינוי/שיפוע של פונקציה |
| קשרים בין פונקציות | השוואה בין פונקציות |
ארגון כיתה מומלץ:
מומלץ להזכיר לתלמידים מה נעשה באשכולות א' וב' ולומר מה נעשה באשכול ג':
באשכול א' – "כיצד לחשב מס הכנסה ומשכורת לאחר ניכוי מס הכנסה", ראינו כיצד מחשבים מס הכנסה ושכר של עובדים אחרי ניכוי מס הכנסה. באשכול ב' – "מס הכנסה בייצוגים שונים", חישבנו את הסכום שינוכה ממשכורת כלשהי עבור מס הכנסה באופן כללי, בעזרת ייצוגים שונים של פונקציה.
בפעילות זו נרצה למצוא ביטויים אלגבריים גם לפונקציה המייצגת את הקשר בין משכורת הברוטו לבין המשכורת לאחר ניכוי מס ההכנסה ולמצוא כמה שיותר קשרים בין שתי הפונקציות.
מומלץ לתת לתלמידים זמן לקרוא שוב את המידע הנתון ולוודא שהמושגים ברורים. פתרון בעיות המטרה יתבצע בקבוצות. לבסוף מומלץ שוב לערוך דיון במליאה.
ניהול השיעור: המורה יאפשר לתלמידים לקרוא ולהבין את המידע הנתון, להתמודד עם בעיות המטרה בקבוצות, כשבאפשרותם להיעזר במדרגות. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות. יש לאפשר שימוש במחשבון. אחרי העבודה בקבוצות ייערך דיון במליאה.
סרטונים לשילוב בפתיחה או בהמשך:
מומלץ לצפות בסרטונים בכיתה או בבית.
סרטון 1: לקבלת סקירה אודות חינוך פיננסי – מושגים בסיסיים.
https://www.youtube.com/watch?v=fnOj83BY918
סרטון 2: להסבר על מס פרוגרסיבי ומדרגות מס.
https://www.youtube.com/watch?v=kGD4gofGYMQ
אשכול מס הכנסה ג – קשר בין מס הכנסה ומשכורת אחרי מס
אשכול ג' (מתוך 4 אשכולות).
הערה: מומלץ לפתור את הבעיות באשכולות מס הכנסה א' ומס הכנסה ב' לפני פתרון הבעיות באשכול זה.
הגדרות יסוד
- משכורת ברוטו: השכר הכולל שמשולם לעובד, לפני שהופחתו ממנו ניכויים מהשכר, כגון מס הכנסה, ביטוח לאומי וביטוח בריאות.
- מס הכנסה: מס שמטילה המדינה על שכר העבודה של כל אחד מהאזרחים שלה (*).
- מדרגות מס: שיטה לחישוב מס הנהוגה במדינת ישראל ובה מחשבים את גובה התשלום של מס ההכנסה לפי גובה השכר.
- טבלת מדרגות מס: טבלה שמציגה את אחוזי המס שיש לנכות לפי גודל השכר.
להלן טבלת מדרגות מס (מתוך האתר כל זכות).
את המידע בטבלה ניתן לפרש באופן הבא:
- על הכנסה של סכום עד 6,330 ₪ לחודש יש לנכות 10%;
- על כל שקל נוסף ועד 9,080 ₪ לחודש יש לנכות 14%;
- על כל שקל נוסף ועד 14,580 ₪ לחודש יש לנכות 20%;
וכך הלאה.
מידע זה נכון לשנת 2020
| מספר מדרגת מס | xx משכורת ברוטו (ב-₪) (גבולות מדרגת מס ההכנסה) | אחוז מס ההכנסה |
|---|---|---|
| 1 | 0<x≤6,3300<x≤6,330 | 10%10% |
| 2 | 6,330<x≤9,0806,330<x≤9,080 | 14%14% |
| 3 | 9,080<x≤14,5809,080<x≤14,580 | 20%20% |
| 4 | 14,580<x≤20,26014,580<x≤20,260 | 31%31% |
| 5 | 20,260<x≤42,16020,260<x≤42,160 | 35%35% |
| 6 | 42,160<x≤54,30042,160<x≤54,300 | 47% |
| 7 | x>54,300 | 50% |
1. בעיית מטרה 1
לפניכם טבלה המתארת את מס ההכנסה בהתאם למדרגות מס ההכנסה השונות ואת הביטויים האלגבריים המתאימים לתשלום מס ההכנסה ולמשכורת אחרי ניכוי מס ההכנסה, כאשר x מייצג את גובה משכורת הברוטו החודשית.
- השלימו את הביטויים האלגבריים בטבלה.
(שימו לב: הביטוי המתאים לתשלום מס ההכנסה חושב באשכול ב' וכאן הביטוי מוצג אחרי פישוט).
| מספר מדרגת מס | משכורת ברוטו (ב-₪) (גבולות מדרגת מס ההכנסה) | אחוז מס ההכנסה | ביטוי אלגברי לתשלום מס ההכנסה (ב-₪) | ביטוי אלגברי למשכורת אחרי ניכוי מס הכנסה (ב-₪) |
|---|---|---|---|---|
| 1 | 0<x≤6,330 | 10% | 0.1x | 0.9x |
| 2 | 6,330<x≤9,080 | 14% | 0.14x−253.2 | |
| 3 | 9,080<x≤14,580 | 20% | 0.8x+798 | |
| 4 | 14,580<x≤20,260 | 31% | ||
| 5 | 20,260<x≤42,160 | 35% | 0.35x−3,212.2 | |
| 6 | 42,160<x≤54,300 | 47% | 0.47x−8,271.4 | 0.53x+8,271.4 |
| 7 | x>54,300 | 50% | 0.5x−9,900.4 | 0.5x+9,900.4 |
f(x) – הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין תשלום מס ההכנסה.
g(x) – הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין המשכורת לאחר ניכוי מס ההכנסה.
- השלימו את הגרפים המתאימים ל- f(x) ול- g(x). נמקו.
מומלץ להיעזר ביישומון.
- השלימו בטבלה את הביטויים האלגבריים המתארים את תשלום מס ההכנסה ואת המשכורת אחרי ניכוי מס הכנסה המתאימים לאותה מדרגת מס הכנסה.
- לכל ביטוי שרשמתם יופיע חלק הגרף המתאים במערכת הצירים.
- בסיום לחצו "בדיקה". אם טעיתם – יופיע חיווי
 . נסו שוב.
. נסו שוב. - במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
- התייחסו לשתי הפונקציות f(x) ו- g(x) וענו על השאלות הבאות:
(הסבירו בדרכים שונות ובייצוגים שונים)
1. מצאו קשרים בין שתי הפונקציות.
2. מצאו תכונות משותפות ושונות לשתי הפונקציות.
3. כיצד התכונות שמצאתם באות לידי ביטוי בהקשר של מס ההכנסה?
הידעתם?
פונקציה בנויה מקטעים של פונקציות קוויות בעלות שיפועים שונים נקראת פונקציה קווית למקוטעין.
הפונקציות f(x) ו- g(x) הן פונקציות קוויות למקוטעין.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון לבעיית מטרה 1
דונו עם התלמידים אודות הקשרים שיעלו אודות שתי הפונקציות:
f(x) – הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין תשלום מס ההכנסה.
g(x) – הפונקציה המייצגת את הקשר בין משכורת הברוטו (x) לבין המשכורת לאחר ניכוי מס ההכנסה.
כוונו אותם לתכונות של פונקציות כמו תחומי עליה וירידה, קצב שינוי.
דונו במשמעות התכונות והקשרים בהקשר למס הכנסה. כאשר ישלימו הביטויים המתאימים יופיע חלק הגרף המתאים באותו צבע.
היישומון לפני השלמת הביטויים:
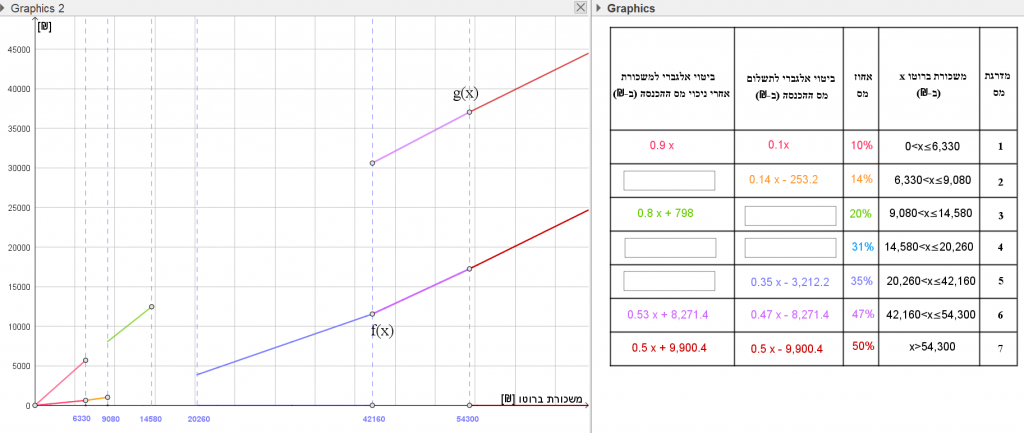
היישומון אחרי השלמת הביטויים:
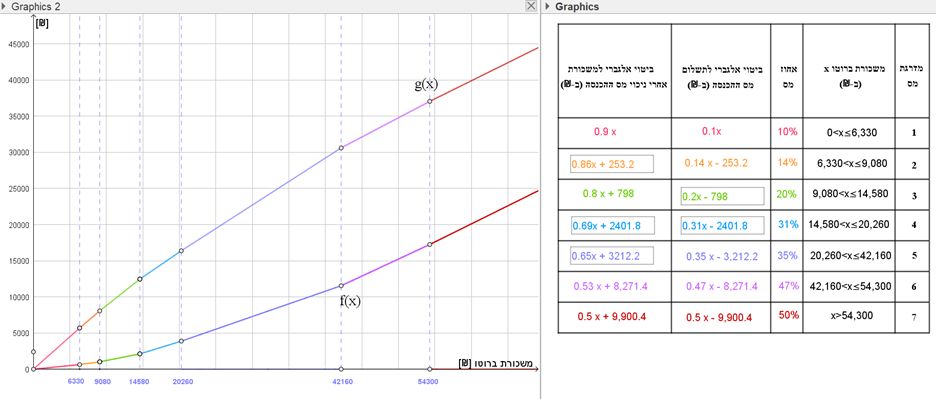
ג. קשרים אפשריים בין שתי הפונקציות:
- סכום השיפועים בכל אחת ממדרגות המס הוא 1.
- תכונות משותפות לשתי הפונקציות: שתי הפונקציות מוגדרות עבור x≥0, חיוביות, עולות, קוויות למקוטעין.
- הסכום של שתי הפונקציות הוא x.
תכונות שונות לשתי הפונקציות:
- בפונקציה f(x), המייצגת את הקשר בין משכורת הברוטו לבין תשלום מס ההכנסה קצב השינוי גדל. המשמעות היא שככל שמשכורת הברוטו גדלה, כך אחוז המס שמשלמים עבור מדרגת מס זו גדל אף הוא.
- בפונקציה g(x), המייצגת את הקשר בין משכורת הברוטו לבין המשכורת לאחר ניכוי מס ההכנסה, קצב השינוי הולך וקטן. המשמעות היא שככל שמשכורת הברוטו גדלה, כך התוספת למשכורת אחרי ניכוי מס ההכנסה עולה בקצב קטן יותר.
- הסכום הקבוע, המנוכה במדרגת מס מסוימת (האיבר החופשי), זהה לסכום שמוחזר למשכורת אחרי ניכוי המס, באותה מדרגת המס.
מטרות בעיית מטרה 1
באשכול ב' התלמידים רשמו ביטויים אלגבריים המייצגים את תשלום מס ההכנסה במדרגות המס השונות.
באשכול זה, המטרה של בעיית מטרה 1 היא שתלמידים ישלימו את הביטויים המתאימים למשכורת אחרי ניכוי מס הכנסה, ישלימו גם את הגרפים המתאימים ויתבוננו בביטויים האלגבריים ובשני הגרפים של הפונקציות (תשלום מס הכנסה ומשכורת אחרי ניכוי מס הכנסה) וימצאו קשרים ביניהם, תכונות משותפות ושונות ומשמעות התכונות בהקשר של מס ההכנסה.
בשלב זה התלמידים אמורים להבין את משמעות המיסוי הפרוגרסיבי. כלומר, כאשר משכורת הברוטו גדלה גם המשכורת אחרי ניכוי מס הכנסה גדלה. התלמידים אמורים לקשר הבנה זו לייצוגים של הפונקציה. למשל, בכל חלק תחום של הפונקציה g(x), המתארת את המשכורת אחרי ניכוי מס הכנסה, מופיע ביטוי אלגברי מהצורה ax+b ומתקיים a>0 ולכן הפונקציה עולה.
לרשותם יישומון בו הם יכולים להיעזר.
1.1 מדרגה 1 לבעיית מטרה 1
רון ודפנה עובדים בחברת תיירות "סביב העולם ב- 80 יום".
להלן משכורות הברוטו החודשיות שלהם:
רון – 12,000 ₪
דפנה – 15,580 ₪.
- מהי מדרגת המס שלפיה יש לחשב את מס ההכנסה של כל אחד מהם?
- בחרו מבין הביטויים הבאים את הביטוי המתאים לחישוב המשכורת לאחר ניכוי מס הכנסה של כל אחד מהם.
(5) 0.2x−798 (3) 0.31x−2,547.6 (1) 0.69x−2,401.8 (6) 0.8x−798 (4) 0.69x+2,401.8 (2) 0.8x+798
הביטוי המתאים לחישוב המשכורת של רון לאחר ניכוי מס הכנסה הוא: _____________
הביטוי המתאים לחישוב המשכורת של דפנה לאחר ניכוי מס הכנסה הוא: _____________
- עבור התחום שבו נמצאת משכורת הברוטו שלו רון, מצאו קשרים בין הביטוי המתאים לתשלום מס ההכנסה לבין הביטוי המתאים למשכורת אחרי תשלום מס הכנסה.
(הסבירו בדרכים שונות ובייצוגים שונים).
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
מדרגות המס להכנסה מיגיעה אישית
| מספר מדרגת מס | x משכורת ברוטו (ב-₪) (גבולות מדרגת מס ההכנסה) | אחוז מס ההכנסה |
|---|---|---|
| 1 | 0<x≤6,330 | 10% |
| 2 | 6,330<x≤9,080 | 14% |
| 3 | 9,080<x≤14,580 | 20% |
| 4 | 14,580<x≤20,260 | 31% |
| 5 | 20,260<x≤42,160 | 35% |
| 6 | 42,160<x≤54,300 | 47% |
| 7 | x>54,300 | 50% |
מקור הטבלה: כל זכות
פתרון למדרגה 1 של בעיית מטרה 1
מדרגת המס שלפיה יש לחשב את מס ההכנסה שרון צריך לשלם היא מדרגה 3 ומדרגת המס שלפיה יש לחשב את מס ההכנסה שדפנה צריכה לשלם היא מדרגה 4.
הביטויים המתאימים:
עבור רון
הביטוי לחישוב של מס ההכנסה הוא: 633+385+0.2(x−9,080)
(הדרך מפרטת את שלבי החישוב מכל מדרגה).
הביטוי לחישוב המשכורת לאחר ניכוי מס ההכנסה הוא ביטוי (2): 0.8x+798.
ועבור דפנה
הביטוי לחישוב של מס ההכנסה הוא: 633+385+1,100+0.31(x−14,580).
הביטוי לחישוב המשכורת לאחר ניכוי מס ההכנסה הוא ביטוי (4): 0.69x+2,401.8.
מטרות מדרגה 1 של בעיית מטרה 1
מטרת הבעיה היא להתמקד בשתי מדרגות מס ולהוביל את התלמידים לבניית הביטויים המתאימים לפונקציה g(x) בתחומים אלו. התלמידים מתבקשים לבחור את הביטוי המתאים לחישוב מס הכנסה של משכורות ברוטו של רון – 12,000 ₪ ועבור דפנה – 15,580 ₪, כאשר x מייצג את משכורת הברוטו.
לאחר מכן הם מתבקשים למצוא קשרים בין שתי הפונקציות רק עבור מדרגת המס השלישית וזאת כהכנה לבעיית המטרה בה ירחיבו לשאר מדרגות המס.
1.2 מדרגה 2 לבעיית מטרה 1
דפנה עובדת בחברת תיירות "סביב העולם ב- 80 יום".
משכורת הברוטו החודשית שלה היא 14,580 ₪.
היא קיבלה העלאה, משכורתה החדשה היא x שקלים
14,580<x≤20,260.
- מהו המס ששילמה לפני ההעלאה?
- רשמו ביטוי אלגברי המתאים לתשלום מס ההכנסה שלה לאחר ההעלאה.
- רשמו ביטוי אלגברי המתאים לחישוב המשכורת שלה אחרי תשלום מס ההכנסה לאחר ההעלאה.
- מצאו קשרים בין הביטויים שמצאתם בסעיפים ב' וג'. (הסבירו בדרכים שונות ובייצוגים שונים).
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 3.
מדרגות המס להכנסה מיגיעה אישית
| מספר מדרגת מס | x משכורת ברוטו (ב-₪) (גבולות מדרגת מס ההכנסה) | אחוז מס ההכנסה |
|---|---|---|
| 1 | 0<x≤6,330 | 10% |
| 2 | 6,330<x≤9,080 | 14% |
| 3 | 9,080<x≤14,580 | 20% |
| 4 | 14,580<x≤20,260 | 31% |
| 5 | 20,260<x≤42,160 | 35% |
| 6 | 42,160<x≤54,300 | 47% |
| 7 | x>54,300 | 50% |
מקור הטבלה: כל זכות
פתרון למדרגה 2 של בעיית מטרה 1
בסעיף א על התלמידים לחשב את מס ההכנסה שדפנה אמורה לשלם כאשר משכורת הברוטו שלה היא קצה מדרגת המס השלישית.
בסעיף ב על התלמידים לכתוב ביטוי עבור מס ההכנסה שדפנה אמורה לשלם כאשר קיבלה העלאה ומשכורת הברוטו שלה נמצאת במדרגת המס הרביעית.
בסעיף ג על התלמידים לכתוב ביטוי עבור המשכורת אחרי תשלום מס ההכנסה (במדרגת המס הרביעית)
ובסעיף ד למצוא קשרים בין שני הביטויים.
- המס ששילמה דפנה לפני ההעלאה:
633+385+0.2(14,580−9,080)=633+385+1,100=2,118.
- הביטוי המתאים לתשלום מס ההכנסה שלה לאחר ההעלאה הוא:
633+385+1,100+0.31(x−14,580)
או 0.31x−2,401.8.
- הביטוי המתאים לחישוב המשכורת שלה אחרי תשלום מס ההכנסה שלה לאחר ההעלאה הוא:
0.69x+2,401.8.
- קשר אפשרי אחד יכול להיות שהסכום של שני הביטויים הוא x:
0.31x−2,401.8+0.69x+2,401.8=x.
מטרות מדרגה 2 של בעיית מטרה 1
בבעיה זו מתמקדים בדפנה שמשכורתה ברוטו היא 14,580 ₪ (קצה של מדרגת המס השלישית). התלמידים נדרשים לחקור מה קורה לתשלום מס ההכנסה ולמשכורת אחרי תשלום מס ההכנסה לאחר שקיבלה העלאה למשכורת ולמצוא קשרים ביניהם. הרעיון הוא להוביל את התלמידים לבניית הביטויים המתאימים רק עבור מדרגת המס הרביעית וזאת כהכנה לבעיית המטרה בה ירחיבו לשאר מדרגות המס.
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית מטרה 1.
מדרגות המס להכנסה מיגיעה אישית
| מספר מדרגת מס | x משכורת ברוטו (ב-₪) (גבולות מדרגת מס ההכנסה) | אחוז מס ההכנסה |
|---|---|---|
| 1 | 0<x≤6,330 | 10% |
| 2 | 6,330<x≤9,080 | 14% |
| 3 | 9,080<x≤14,580 | 20% |
| 4 | 14,580<x≤20,260 | 31% |
| 5 | 20,260<x≤42,160 | 35% |
| 6 | 42,160<x≤54,300 | 47% |
| 7 | x>54,300 | 50% |
מקור הטבלה: כל זכות
פתרון למדרגה 3 של בעיית מטרה 1
| משכורת ברוטו | הביטוי המתאים לחישוב המשכורת אחרי תשלום מס הכנסה |
|---|---|
| 4,500 ₪ | 0.9x |
| 6,800 ₪ | 0.86x+253.2 |
| 9,500 ₪ | 0.8x+798 |
| 15,000 ₪ | 0.69x+2,401.8 |
מטרות מדרגה 3 של בעיית מטרה 1
מדרגה זו מיועדת לתלמידים שלא הצליחו לפתור את בעיית המטרה ואת שתי הבעיות במדרגות 1 ו-2. בבעיה זו מוצגות 4 משכורות ממדרגות מס הכנסה שונות: 1,2,3,4 וכן ביטויים המתאימים לחישוב המשכורת אחרי תשלום מס ההכנסה. התלמידים מתבקשים להתאים בין המשכורות לבין הביטויים. המטרה היא להכין אותם לפתרון הבעיות הקודמות.
2. בעיית מטרה 2
- לפי טבלת מדרגות המס דורית אמורה לשלם 2,500 ₪ מס הכנסה.
1. קבעו באיזו מדרגת מס נמצאת המשכורת של דורית?
2. כמה אחוזים, מתוך משכורתה של דורית, מהווה התשלום שלה למס ההכנסה?
- ידוע כי המשכורת של דורון לאחר ניכוי מס הכנסה היא 9,000 ₪.
1. קבעו באיזו מדרגת מס נמצאת המשכורת של דורון?
2. כמה אחוזים, מתוך משכורתו של דורון, מהווה התשלום שלו למס ההכנסה?
- סמנו V בתיבות הבחירה: "נקודה על f(x)", ו-"נקודה על g(x)".
במערכת הצירים תופיע נקודה על הגרף המתאים ושני קווים מקווקוים מקבילים לצירים, המסמנים את שיעורי הנקודה. - שנו את מיקום הנקודה על הגרף על ידי גרירת הנקודה לאורך ציר ה-y ועקבו אחרי השינוי בשיעורי הנקודה.
- ניתן לדייק יותר בשיעורי הנקודה על ציר ה-y, על ידי לחיצה עליה בעכבר, ואז באמצעות שימוש בחיצים שבמקלדת.
- במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
- במידת הצורך, פתרו את השאלות במדרגה 1
פתרון לבעיית מטרה 2
מומלץ להשתמש בכפתור "zoom in".
- דורית אמורה לשלם 2,500 ₪ מס הכנסה.
סעיף 1
כדי להחליט לאיזו מדרגת מס היא מגיעה אפשר להיעזר ביישומון ולהזיז את הנקודה על הגרף של f(x) כך שערך ה- y שלה יהיה 2,500 ₪. כך מגלים שהמשכורת של דורית נמצאת במדרגת המס הרביעית. להלן החישוב של השכר שלה: 0.31x−2,401.8=2,500. כך מתקבל x=15,812.26.
כלומר, המשכורת של דורית לפני ניכוי מס היא: 15,812.26 ₪.
סעיף 2
להלן החישוב של האחוז: 2,50015,812.26⋅100%=15.81%
- המשכורת של דורון לאחר ניכוי מס הכנסה היא 9,000 ₪.
סעיף 1
כדי להחליט באיזו מדרגת מס נמצאת המשכורת של דורון אפשר להיעזר ביישומון ולהזיז את הנקודה על הגרף של g(x) כך שערך ה- y שלה הוא 9,000 ₪. כך מגלים שהמשכורת של דורון נמצאת במדרגת המס השלישית. להלן החישוב של השכר שלו: 0.8x+798=9,000. כך מתקבל x=10,252.5.
כלומר, המשכורת ברוטו של דורון לפני ניכוי מס היא: 10,252.5 ₪.
סעיף 2
להלן החישוב של האחוז: 10,252.5−9,00010,252.5⋅100%=12.216%
מטרות בעיית מטרה 2
המטרה של בעיית המטרה 2 היא שתלמידים ישתמשו בתובנות אליהן הגיעו עד כה ויבינו כי אחוז המס המשולם במדרגת מס מסוימת איננו זהה לאחוז שהתשלום למס ההכנסה מהווה מתוך משכורת הברוטו.
לרשותם יישומון בו הם יכולים להיעזר – אותו יישומון של בעיית מטרה 1. במידה והביטויים שהושלמו בבעיית מטרה 1 נכונים, יופיעו נקודות על הגרפים נקודה על הגרף f(x) ונקודה על הגרף g(x). התלמידים יוכלו לנוע על הגרפים כדי לענות על השאלות.
2.1 מדרגה 1 לבעיית מטרה 2
x מייצג את גובה משכורת הברוטו החודשית ב-₪.
ביישומון שלפניכם טבלה המתארת את הביטויים האלגבריים המתאימים לתשלום מס ההכנסה ולמשכורת אחרי ניכוי מס ההכנסה.
כמו כן, מוצגים באותה מערכת צירים שני גרפים:
האחד מתאר את הקשר בין משכורות הברוטו לבין מס ההכנסה והשני מתאר את הקשר בין משכורת הברוטו לבין המשכורת לאחר ניכוי מס ההכנסה.
- סמנו V בתיבות הבחירה: "נקודה על f(x)", ו-"נקודה על g(x)". במערכת הצירים תופיע נקודה על הגרף המתאים ושני קווים מקווקוים מקבילים לצירים, המסמנים את שיעורי הנקודה.
- שנו את מיקום הנקודה על הגרף על ידי גרירת הנקודה לאורך ציר ה-y ועקבו אחרי השינוי בשיעורי הנקודה.
- ניתן לדייק יותר בשיעורי הנקודה על ציר ה-y, על ידי לחיצה עליה בעכבר, ואז באמצעות שימוש בחיצים שבמקלדת.
- במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
- מס ההכנסה שנועה אמורה לשלם הוא 866.8 ₪.
בחרו מבין הביטויים שבטבלה את הביטוי שמתאים לחישוב מס ההכנסה שעל נועה לשלם. - משכורתו של גדעון לאחר ניכוי מס ההכנסה היא 13,000 ₪.
בחרו מבין הביטויים שבטבלה את הביטוי שמתאים לחישוב משכורת הברוטו של גדעון.
נמקו את בחירתכם.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 2.
פתרון למדרגה 1 של בעיית מטרה 2
- נועה אמורה לשלם 866.8 ₪ למס הכנסה. מאחר וסכום זה גבוה מ- 633 ₪, משכורת הברוטו שלה לא נמצאת במדרגת המס הראשונה. מאחר וסכום זה נמוך מ- 1,018 ₪, היא נמצאת במדרגת המס השנייה. לכן הביטוי שמתאים לחישוב מס ההכנסה שעל נועה לשלם הוא: 0.14x−253.2. אפשר להציב ולבדוק או לנוע על הגרף המתאים ביישומון ולבדוק.
- משכורתו של גדעון לאחר תשלום מס ההכנסה היא 13,000 ₪. הוא נמצא לפחות במדרגת המס השלישית. מהצבה בביטוי 0.8x+798, המתאים לחישוב המשכורת אחרי תשלום מס ההכנסה עבור מדרגת המס השלישית, נקבל כי משכורת הברוטו היא 15,252.5 ₪. ולכן לא מתאימה למדרגת מס זו.
מכאן שיש לחשב לפי הביטוי 0.69x+2,401.8, שמתאים לחישוב המשכורת אחרי תשלום מס ההכנסה עבור מדרגת המס הרביעית. ואכן אחרי הצבה מתקבל כי משכורת הברוטו היא 15,359.71 ₪. משכורת זו מתאימה למדרגת המס הרביעית.
החישוב:
0.69x+2,401.8=13,000
⇓
x=15,359.71
אפשר להציב ולבדוק או לנוע על הגרף המתאים ביישומון ולבדוק.
מטרת מדרגה 1 של בעיית מטרה 2
מטרת הבעיה היא להיעזר בטבלה המלאה המתארת את הביטויים המתאימים לתשלום מס ההכנסה ולמשכורת אחרי תשלום מס ההכנסה במדרגות השונות וכן בגרפים המתאימים. ולהוביל את התלמידים לבחור את הביטויים המתאימים לחישוב מס ההכנסה ולחישוב המשכורות אחרי תשלום מס ההכנסה.
לרשותם יישומון בו הם יכולים להיעזר.












