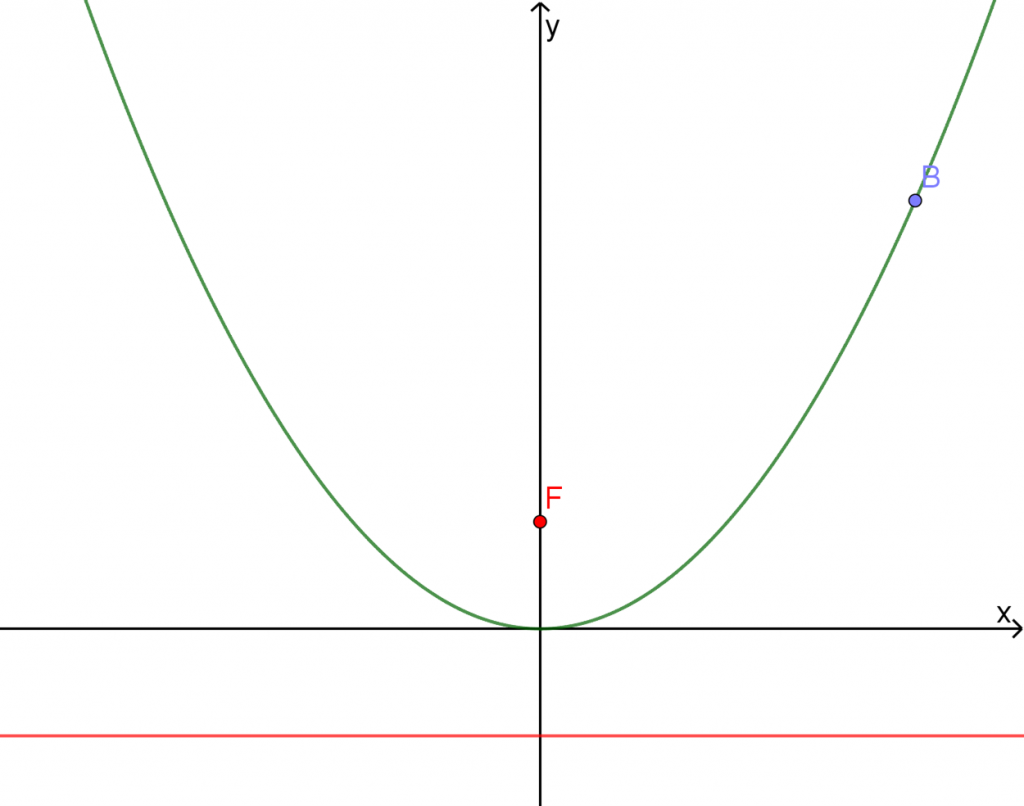
عنقود مرايا كقطوع مكافئة - بؤرة، دليل وما بينهما - جزء ت
(يمكن الضغط على الرسم وتكبيرها)
| تعبير جبري للقطع المكافئ | إحداثيات نقطة Bعلى القطع المكافئ | إحداثيات البؤرة (F) |
|---|---|---|
| p(x)=0.25x2 | (1,0.25) | |
| p(x)=x2 | (1,1) | |
| p(x)=2x2 | (1,2) | |
| p(x)=4x2 | (1,4) | |
| p(x)=ax2 | (1,a) |
- كلما كانت المرآة على شكل القطع المكافئ أوسع، هل تكون البؤرة أقرب إلى رأس القطع المكافئ أم أبعد عنه؟ علّلوا إجابتكم.
- إذا حليّتم مسألة هدف 2، انتقلوا إلى ماذا يمكن أن نسأل أيضًا.
- اختاروا إحداثي x للنقطة B:
بواسطة جرّ النقطة B على القطع المكافئ، أو بواسطة شريط الجر x(B). - غيّروا قيم شريط الجر a ، وافحصوا تأثير قيمة a على مكان البؤرة (F) والدليل (الخط m).