אשכול ציון במבחן ריצה - למורה
יישומונים
- – – – – –
הנחיות למורה
אשכול 2 – מתוך 2 אשכולות.
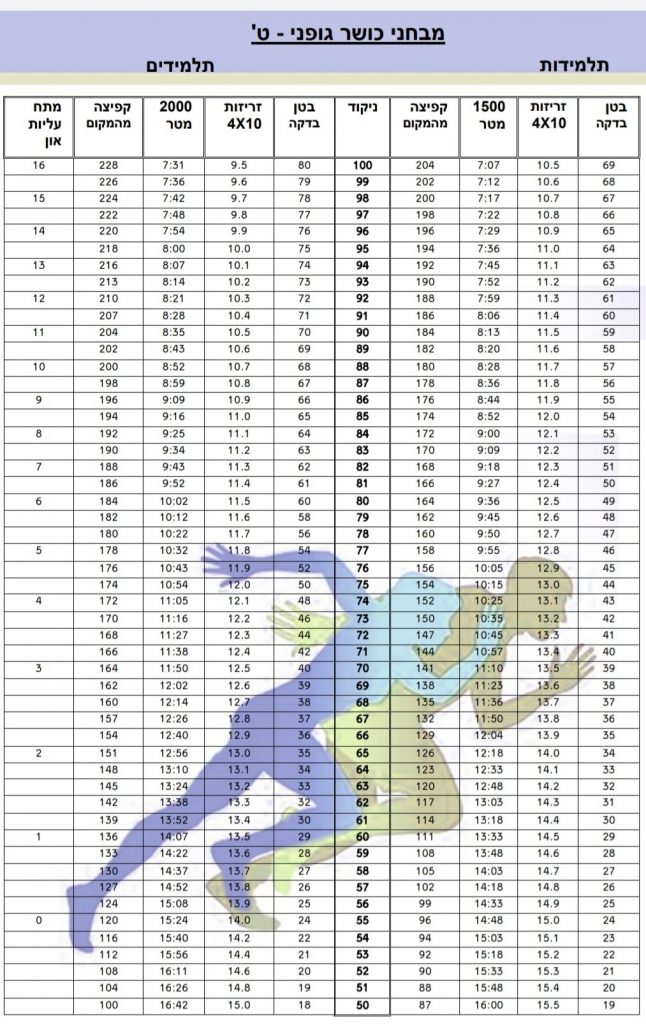
אשכול זה עוסק במבחני כושר גופני לכיתה ט'. בטבלה מפורטים ציונים בתרגילים שונים בחינוך גופני. באשכול זה נתמקד במבחן ריצה עבור בנים 2000 מטר ועבור בנות 1500 מטר.
יחידה:
תרבות וספורט
כיתה מומלצת:
כיתה ח / כיתה ט
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
- ספורט וחברה.
- קריאת ציונים מטבלה נתונה עבור מבחן ריצה.
- יכולת לעבור בין ייצוגים שונים של מידע.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| קריאת נתונים מטבלה | – טבלה – נתונים | קריאה והבנה של נתונים המוצגים בטבלה |
| משוואות ופתרונן | – נעלם – משוואה – פתרון של משוואה – שקילות של משוואות | – שינוי נושא נוסחה – יצירת משוואות שקולות |
| שאלות מילוליות שניתנות לפתרון באמצעות משוואות ממעלה ראשונה בנעלם אחד | – ביטוי אלגברי – משוואה – פתרון של משוואה | – ייצוג הנתון הלא ידוע בנעלם – ייצוג נתונים נוספים בביטויים אלגבריים – יצירת משוואה שבאמצעותה ניתן לפתור את השאלה |
| פתרון בעיות תנועה | – מהירות – זמן – דרך | מציאת אחד המשתנים במשוואה \(s=v\cdot t\) כאשר נתונים שני האחרים |
| יחס בין מספרים | – יחס – מנה – השוואה | – מציאת יחס בין מספרים – צמצום והרחבה של יחס |
| פרופורציה | פרופורציה | מציאת שוויון בין יחסים במושגים: מהירות, זמן, דרך |
| יחס ישר/הפוך | – יחס ישר – יחס הפוך | – זיהוי יחס ישר/הפוך בין גדלים מספריים – זיהוי יחס ישר/הפוך בין ביטויים s , v , t |
| הנמקה של טענות, הפרכה של טענות | דוגמה נגדית | – אבחנה בין נכונות של טענות: (א) טענה שנכונה בכל מקרה (ב) טענה שאיננה נכונה בכל מקרה (ג) טענה שאיננה נכונה בכל מקרה אבל ייתכנו מקרים פרטיים שבהם היא נכונה. – אבחנה בין טענות נכונות וטענות שגויות |
מטרות האשכול:
- לקרוא נתונים רלוונטיים מתוך מאגר גדול של נתונים.
- לעבור בין יחידות מידה.
- לנתח את הקשרים בין מהירות, זמן, דרך וציון עבור מבחן ריצה.
- להבחין בקיום יחס ישר או יחס הפוך בין המשתנים: מהירות, זמן, דרך.
- להשוות בין יחסים.
הערה: מומלץ להציע לתלמידים לעבוד עם מספרים מעורבים (ולא מספרים עשרוניים) ולהשתמש במחשבון בכפתור של מספר מעורב.
מערך דידקטי מומלץ:
ארגון הכיתה:
מומלץ להזכיר לתלמידים מה נעשה באשכול ציון במבחני כושר גופני, שעסק בציון במבחן כושר גופני ובו הוצגה הטבלה המופיעה באשכול זה.
מומלץ לתת לתלמידים זמן לקרוא את המידע המוצג בטבלה, לחדד את האבחנה בין מרחק הריצה של בנים לבין מרחק הריצה של בנות ולוודא שהם יודעים לקרוא מהטבלה: את זמן הריצה בהינתן הציון, או את הציון בהינתן זמן הריצה.
פתרון בעיות המטרה יתבצע בקבוצות. אחרי העבודה בקבוצות ייערך דיון במליאה.
ניהול השיעור: המורה יאפשר לתלמידים לקרוא ולהבין את המידע הנתון, להתמודד עם בעיות המטרה בקבוצות, כשבאפשרותם להיעזר במדרגות. המדרגות מיועדות לשתי בעיות המטרה. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות. יש לאפשר שימוש במחשבון.
שאלות מומלצות לדיון כיתתי:
- מה ההבדל בין בנים לבנות בהקשר למבחן הריצה?
- בין אילו משתנים (מהירות, זמן, דרך) מתקיים יחס ישר ובין אילו יחס הפוך? הסבירו.
הערה: באשכול זה נשתמש במילה "מהירות" כאשר הכוונה ל"מהירות ממוצעת".
העשרה:
אשכול ציון במבחן ריצה
תיאור סיטואציה
לפניכם טבלה בה נעזרים מורים לחינוך גופני ובה מתוארים מדדים לקבלת ציון בתרגילים שונים בחינוך גופני.
הקריטריונים שונים עבור בנים ועבור בנות.
בכיתות ט' לצורך מתן ציונים במבחני כושר גופני, תלמידים (בנים) נבחנים ב-5 מדדים, ותלמידות (בנות) נבחנות ב-4 מדדים.
כדי לקבל ציון סופי בכושר גופני, המורה משקלל את הציונים בכל המדדים (ציון ממוצע).
לדוגמה: בתרגיל "בטן בדקה" כדי לקבל ציון 90 תלמידה צריכה לעשות 59 כפיפות בטן בדקה ואילו תלמיד צריך לעשות 70.
הזמנים בטבלה מופיעים בתצוגה של שעון דיגיטלי.
באשכול זה נתמקד במבחן ריצה המופיע בטבלה, כאשר בנים נבחנים בריצה של 2000 מטרים ובנות בריצה של 1500 מטרים.
תזכורת: המהירות הממוצעת מתארת את מהירותו של גוף לאורך דרך מסוימת.
\(v=\Large\frac{s}{t}\)
v – מהירות ; s – מרחק ; t – זמן
באשכול זה נשתמש במילה "מהירות" כאשר הכוונה ל"מהירות ממוצעת".
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
- אחרי שפתרתם את בעיית המטרה, המשיכו לבעיית הסיכום.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
הצעה לפתרון בעיית המטרה
סעיף א
מוצגות שתי דרכים לפתרון.
דרך א': חישובים
אפשר לחשב באופנים שונים:
- חישוב המהירות של דן, זוהי גם המהירות של רקפת, חישוב הזמן של רקפת לפי המהירות והדרך, בדיקת הציון בטבלה והשוואתו לציון הנתון – 95.
- חישוב המהירויות של שניהם על פי הציונים הנתונים ובדיקה אם הן שוות.
| ציון נתון | מרחק ריצה (במטרים) | זמן ריצה (מהטבלה) | זמן ריצה בדקות | חישוב המהירות (במטר לדקה) על ידי שימוש בנוסחה |
|
|---|---|---|---|---|---|
| דן | 59 | 2000 | 14:22 | \(14\Large\frac{22}{60}\) | \(v=\Large\frac{2000}{14\Large\frac{22}{60}}\normalsize=139\Large\frac{91}{431}\) |
| רקפת | 95 | 1500 | 7:36 | \(7\Large\frac{36}{60}\) | \(v=\Large\frac{1500}{7\Large\frac{36}{60}}\normalsize=197\Large\frac{7}{19}\) |
מסקנה: דן לא צודק מאחר והמהירויות שונות.
דרך ב': השוואת יחסי זמנים ליחסי הדרכים עבור מהירות זהה
בדרך זו התלמידים ישתמשו בתובנה כי עבור מהירות זהה מתקיים יחס ישר בין הזמן לבין הדרך – יחס הזמנים שווה ליחס הדרכים (\(s=v\cdot t\)).
כלומר: עבור מהירות זהה מתקיים כי יחס הזמנים של דן ורקפת שווה ליחס הדרכים שלהם.
\(\Large\frac{s(ןד)}{s(תפקר)}\normalsize=\Large\frac{2000}{1500}\normalsize=\Large\frac{4}{3}\)
התבוננות בטבלה ומציאת הזמנים המתאימים לציונים הנתונים.
\(\Large\frac{t(ןד)}{t(תפקר)}\normalsize=\Large\frac{14\Large\frac{22}{60}}{7\Large\frac{36}{60}}\normalsize=\Large\frac{431}{228}\normalsize\ne\Large\frac{4}{3}\)
מסקנה: דן לא צודק מאחר והיחסים שונים.
סעיף ב
מוצגות שתי דרכים לפתרון.
דרך א': חישובים
| ציון נתון | מרחק ריצה (במטרים) | זמן ריצה (מהטבלה) | זמן ריצה בדקות | חישוב המהירות (במטר לדקה) על ידי שימוש בנוסחה |
|
|---|---|---|---|---|---|
| יוסי | 79 | 2000 | 10:12 | \(10\Large\frac{12}{60}\) | \(v=\Large\frac{2000}{10\Large\frac{12}{60}}\normalsize=196\Large\frac{4}{51}\) |
| דנה | 79 | 1500 | 9:45 | \(9\Large\frac{45}{60}\) | \(v=\Large\frac{1500}{9\Large\frac{45}{60}}\normalsize=153\Large\frac{11}{13}\) |
מכאן:
\(\Large\frac{v(יסוי)}{v(הנד)}\normalsize=\Large\frac{196\Large\frac{4}{51}}{153\Large\frac{11}{13}}\normalsize=\Large\frac{65}{51}\)
דרך ב': השוואת יחסי המהירויות ליחסי הזמנים עבור דרך זהה
בדרך זו התלמידים ישתמשו בתובנות הבאות:
- עבור מהירות זהה, מתקיים יחס ישר בין הזמן לבין הדרך – יחס הזמנים שווה ליחס הדרכים \((s=v \cdot t)\).
- עבור דרך זהה, מתקיים יחס הפוך בין המהירות לבין הזמן – יחס המהירויות הפוך ליחס הזמנים.
כלומר: עבור דרך זהה, מתקיים כי יחס הזמנים של יוסי ודנה הפוך ליחס המהירויות.
על פי הנתון יוסי רץ דרך של 2000 מטרים במשך \(10\Large\frac{12}{60}\) דקות. לכן, לו היה צריך לרוץ 1500 מטרים, היה רץ בזמן \(\Large\frac{3}{4}\normalsize\cdot10\Large\frac{12}{60}\)
\(\Large\frac{v(יסוי)}{v(הנד)}\normalsize=\Large\frac{t(הנד)}{\Large\frac{3}{4}\cdot t(יסוי)}\normalsize=\Large\frac{9\Large\frac{45}{60}}{\Large\frac{3}{4}\cdot10\Large\frac{12}{60}}\normalsize=\Large\frac{65}{51}\)
מטרות בעיית המטרה
המטרות של בעיית המטרה הן:
- למצוא בטבלה את הזמנים המתאימים לציונים הנתונים תוך אבחנה בין בן לבין בת.
- לתרגם את הזמנים לדקות.
- לחשב את המהירויות לפי הנוסחה \(v=\Large\frac{s}{t}\).
- להשוות בין המהירויות.
- לחשב יחס
- להבין את היחסים בין המהירות, הזמן והדרך. מה התנאים לקיום יחס ישר או יחס הפוך.
בסעיף א של בעיית המטרה מתואר מצב בו בן ובת מקבלים ציונים שונים במבחן הריצה. מוצגת טענה כי המהירויות שלהם שוות ועל התלמידים לבחון את נכונות הטענה ולנמק.
בסעיף ב של בעיית המטרה מתואר מצב בו בן ובת מקבלים אותו ציון במבחן הריצה ויש לחשב את יחס המהירויות שלהם.
תלמידים שלא הצליחו להתמודד עם בעיות המטרה יפתרו את בעיות המדרגה.
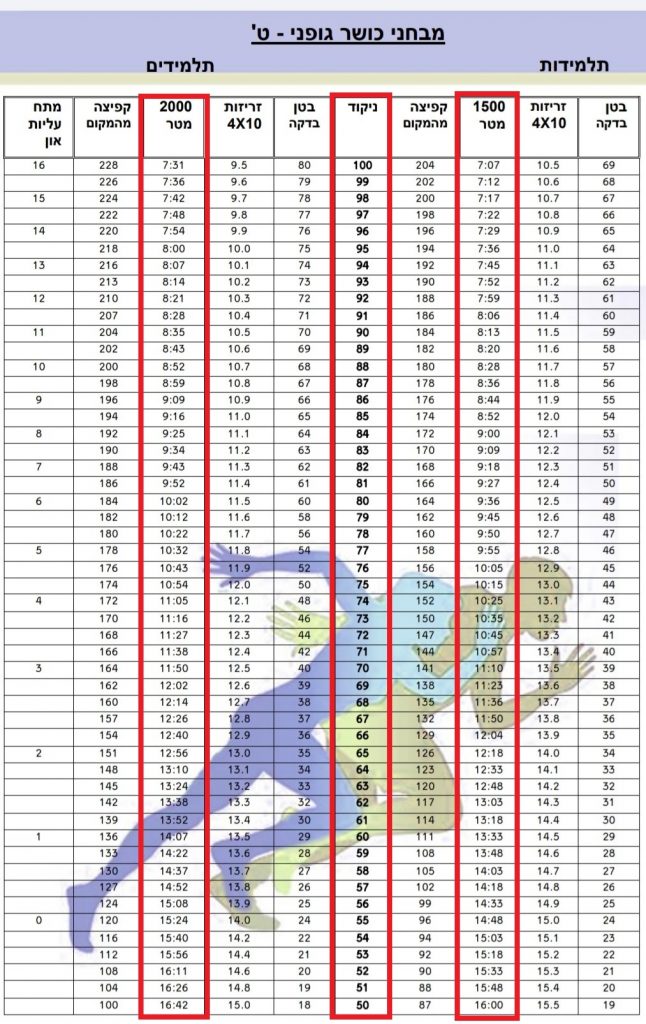
בבעיות המדרגה מוצגת לתלמידים טבלה שבה מודגשות העמודות עם הנתונים הרלוונטיים: ציונים, זמן בנות, זמן בנים.
1.1 מדרגה 1 לבעיית המטרה
בעיה 1.1.1
נורית קיבלה ציון 80 במבחן הריצה וביקשה לרוץ פעם נוספת במטרה לשפר את הציון.
בריצתה השנייה היא רצה במהירות של 160 מטר לדקה. האם נורית שיפרה את ציונה?
בעיה 1.1.2
חיים רץ ריצת 2000 מטרים במהירות של 256.41 מטר לדקה.
איזה ציון קיבל חיים?
בעיה 1.1.3
יעל השתתפה במבחן הריצה פעמיים ורצה באותה מהירות.
ביום הראשון רצה את כל הדרך. ביום השני היא התעייפה והפסיקה לרוץ אחרי שעברה \(\Large\frac{5}{6}\) מהדרך.
בחרו את המספר המבטא את היחס בין זמן הריצה של יעל ביום הראשון לבין זמן הריצה ביום השני. נמקו תשובתכם.
- \(\Large\frac{t (ןושאר\space םוי)}{t (ינש\space םוי)}\normalsize=1 \Large\frac{1}{5}\)
- \(\Large\frac{t (ןושאר\space םוי)}{t (ינש\space םוי)}\normalsize=1 \Large\frac{1}{6}\)
- \(\Large\frac{t (ןושאר\space םוי)}{t (ינש\space םוי)}\normalsize=\Large\frac{5}{6}\)
- \(\Large\frac{t (ןושאר\space םוי)}{t (ינש\space םוי)}\normalsize=\Large\frac{6}{7}\)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית המטרה.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
הצעה לפתרון מדרגה 1 לבעיית המטרה
פתרון בעיה 1.1.1
נתון כי בריצה הראשונה נורית קיבלה ציון 80 ובריצה השנייה מהירותה 160 מטר לדקה ויש לבדוק האם שיפרה את הציון.
דרך א': חישוב המהירות בריצה הראשונה והשוואה למהירות בריצה השנייה
| ציון נתון | מרחק ריצה (במטרים) | זמן ריצה (מהטבלה) | זמן ריצה בדקות | חישוב המהירות (במטר לדקה) על ידי שימוש בנוסחה |
|
|---|---|---|---|---|---|
| נורית ריצה ראשונה | 80 | 1500 | 9:36 | \(9\Large\frac{36}{60}\) | \(v=\Large\frac{1500}{9\Large\frac{36}{60}}\normalsize=156\Large\frac{1}{4}\) |
מאחר ומהירותה עלתה בריצה השנייה (נתונה 160 מטר לדקה) נוכל להסיק כי שיפרה את ציונה.
דרך ב': חישוב זמן בריצה השנייה והשוואה לזמן בריצה הראשונה
| ציון נתון | מרחק ריצה (במטרים) | זמן ריצה בדקות | מהירות (במטר לדקה) | |
|---|---|---|---|---|
| נורית ריצה שניה | 80 | 1500 | \(t=\Large\frac{1500}{160}\normalsize=9\Large\frac{3}{8}\) | 160 |
מאחר ו- \(9\Large\frac{3}{8}\normalsize<9\Large\frac{36}{60}\) כלומר זמן הריצה השנייה קטן מזמן הריצה הראשונה, נוכל להסיק כי שיפרה את ציונה.
פתרון בעיה 1.1.2
נתונה מהירותו של חיים. נתון גם כי אורך הדרך שרץ הוא 2000 מטרים (בנוסף לכך שבטבלה מופיע אורך הדרך). יש לחשב את הציון שלו.
- הצבה בנוסחה \(t=\Large\frac{s}{v}\normalsize\space\Longrightarrow\space t=\Large\frac{2000}{256.41}\normalsize=7.8\)
- תרגום הזמן לדקות \(\Large\frac{8}{10}\normalsize=\Large\frac{48}{60}\) כלומר הזמן הוא 7:48.
- מציאת הציון מהטבלה: הציון של חיים הוא 97.
פתרון בעיה 1.1.3
נתון כי יעל רצה פעמיים. בפעם השנייה רצה רק \(\Large\frac{5}{6}\) מהדרך. יש לבחור מתוך 4 אפשרויות את היחס בין זמני הריצה של יעל.
דרך א': חישוב הזמן בכל אחת מהריצות וחישוב היחס ביניהם
| מרחק ריצה (במטרים) | זמן ריצה בדקות | מהירות (במטר לדקה) | |
|---|---|---|---|
| יעל ריצה ראשונה | 1500 | \(t\space (ןושאר\spaceםוי)=\Large\frac{1500}{v}\) | v |
| יעל ריצה שניה | 1250 | \(t\space (ינש\spaceםוי)=\Large\frac{1250}{v}\) | v |
לכן \(\Large\frac{t(ןושאר\spaceםוי)}{t(ינש\spaceםוי)}\normalsize=\Large\frac{1500}{1250}\normalsize=\Large\frac{6}{5}\).
התשובה הנכונה היא תשובה א.
דרך ב': שימוש בתובנה כי עבור מהירות קבועה יחס הזמנים שווה ליחס הדרכים
יחס הדרכים: \(\Large\frac{s(ןושאר\spaceםוי)}{s(ינש\spaceםוי)}\normalsize=\Large\frac{1500}{1250}\normalsize=\Large\frac{6}{5}\)
לכן, יחס הזמנים: \(\Large\frac{t(ןושאר\spaceםוי)}{t(ינש\spaceםוי)}\normalsize=\Large\frac{6}{5}\)
מטרות מדרגה 1 לבעיית המטרה
המטרות של בעיית מדרגה 1 הן:
- להשתמש בטבלה למציאת הזמן המתאים לציון נתון ולחשב מהירות לפי הנוסחה.
- לחשב זמן למהירות נתונה ולהתאים לו ציון על פי הטבלה.
- לערוך השוואה בין ציונים, זמנים, מהירויות.
- לבחור את יחס הזמנים בהינתן יחס הדרכים.
- להבין כי קיים יחס ישר בין זמן לבין דרך כאשר המהירות קבועה, כלומר: עבור אותה מהירות מתקיים כי יחס הזמנים שווה ליחס הדרכים.
1.2 מדרגה 2 לבעיית המטרה
בעיה 1.2.1
לפניכם זמני הריצה של תלמידים בהצגות שונות.
חלק מהזמנים מופיעים בהצגה עשרונית (למשל 8.6 דקות)
וחלק בהצגה כפי שמראה שעון דיגיטלי (למשל 
)
סדרו אותם מהזמן הקצר ביותר לזמן הארוך ביותר.
א. 8:06 ב. 8.06 ג. 8.1
ד. 8.6 ה. 8.01 ו. 8:36
בעיה 1.2.2
במבחן הריצה, כשהתחיל ירון לרוץ הראה השעון 
כשסיים את הריצה, הראה השעון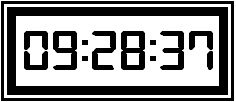 
מה הציון שירון קיבל?
בעיה 1.2.3
הציון של רותי בריצה (1500 מטרים) הוא 83.
- כמה דקות נמשכה ריצתה של רותי. בטאו את התשובה כשבר או כמספר מעורב.
- באיזו מהירות רותי רצה?
- עומרי רץ (2000 מטרים) בזמן זהה לזמן של רותי. באיזו מהירות עומרי רץ?
- מה היחס בין המהירות של עומרי לבין המהירות של רותי?
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית המטרה.
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
הצעה לפתרון מדרגה 2 לבעיית המטרה
פתרון בעיה 1.2.1
נתונים זמנים שונים של ריצה ויש לסדר אותם בסדר עולה.
| הזמן הארוך ביותר | הזמן הקצר ביותר | ||
|---|---|---|---|
| 8:36 | 8:06 | ||
| 8.6 | 8.1 | 8.06 | 8.01 |
פתרון בעיה 1.2.2
נתונים הזמנים של התחלה וסיום ריצה של ירון ויש לחשב את ציונו במבחן הריצה.
שעת התחלה: 9:20:02 שעת סיום: 9:28:37, לכן זמן הריצה הוא 8:35.
מהתבוננות בטבלה, ציונו של ירון הוא 90.
פתרון בעיה 1.2.3
- נתון הציון של רותי במבחן ריצה ויש למצוא בטבלה את זמן הריצה ולתרגם אותו לדקות.
- על התלמיד להשתמש בזמן בדקות שחישב בסעיף א ובעזרת הנוסחה לחשב את המהירות של רותי.
- נתון כי עומרי רץ בזמן זהה לזמן של רותי ויש לחשב את מהירותו.
- יש לחשב את היחס בין המהירות של עומרי לבין המהירות של רותי.
דרך א': חישובים
| ציון נתון | מרחק ריצה (במטרים) | זמן ריצה (מהטבלה) | זמן ריצה בדקות | חישוב המהירות (במטר לדקה) על ידי שימוש בנוסחה |
|
|---|---|---|---|---|---|
| רותי | 83 | 1500 | 9:09 | \(9\Large\frac{9}{60}\) | \(v=\Large\frac{1500}{9\Large\frac{9}{60}}\normalsize=163\Large\frac{57}{61}\) |
| עומרי | 2000 | \(9\Large\frac{9}{60}\) | \(v=\Large\frac{2000}{9\Large\frac{9}{60}}\normalsize\approx218.58\) |
לכן \(\Large\frac{v(ירמוע)}{v(יתור)}\normalsize=\Large\frac{218.57}{163\Large\frac{57}{61}}\normalsize=1.33\)
דרך ב': השוואת יחסי מהירויות ליחסי הדרכים עבור זמן זהה
בדרך זו התלמידים ישתמשו בתובנה כי עבור זמן זהה מתקיים יחס ישר בין המהירות לבין הדרך – יחס המהירויות שווה ליחס הדרכים \((s=v\cdot t)\).
כלומר: עבור זמן זהה מתקיים כי יחס המהירויות של עומרי ורותי שווה ליחס הדרכים שלהם
\(\Large\frac{s(ירמוע)}{s(יתור)}\normalsize=\Large\frac{2000}{1500}\normalsize=\Large\frac{4}{3}\)
מכאן \(\Large\frac{v(ירמוע)}{v(יתור)}\normalsize=\Large\frac{4}{3}\)
מטרות מדרגה 2 לבעיית המטרה
בבעיית מדרגה זו, תחילה התלמידים מתבקשים להשתמש בטבלה למציאת ציון מתאים לזמן מחושב, לקרוא מהטבלה זמן מתאים לציון נתון, לחשב מהירות ורק אחר כך לחשב יחס בין המהירויות.
המטרות של בעיית מדרגה 2 הן:
- לחשב הפרש זמנים נתונים בשעות, דקות, שניות.
- להשתמש בטבלה למציאת הציון המתאים לזמן ריצה נתון.
- לחשב מהירות לפי ציון נתון (למצוא ראשית את הזמן מהטבלה).
- למצוא מהירות מתאימה לזמן נתון.
- לחשב את יחס המהירויות.
- לנסות להגיע להבנה שיחס המהירויות שווה ליחס הדרכים עבור זמן זהה.
2. בעיית סיכום
קבעו עבור כל טענה אם היא נכונה או אינה נכונה. הסבירו בדרכים שונות.
טענה 1: אם המהירות של בן זהה למהירות של בת אז יחס הזמנים הוא \(\Large\frac{t (ןב)}{t (תב)}\normalsize=\Large\frac{4}{3}\).
טענה 2: כדי שבן יקבל ציון זהה לציון של בת עליו לרוץ במשך זמן ארוך יותר.
טענה 3: אם בן ובת רצים אותו מרחק באותו זמן אז הבן יקבל ציון גבוה יותר.
טענה 4: אם בן ובת רצים אותו זמן אז הציון של הבת נמוך מהציון של הבן.
טענה 5: אם בן רץ במהירות גבוהה יותר ממהירותה של בת אז הציון שלו גבוה מציונה של הבת.
- אחרי שפתרתם את בעיית הסיכום, המשיכו למה עוד ניתן לשאול.
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
הצעה לפתרון בעיית הסיכום
הטענות הנכונות הן: 1,2,4.
מטרת בעיית הסיכום
מטרת בעיית הסיכום הינה להגיע למסקנות כלליות מתוך התובנות אליהן הגיעו התלמידים בפתרון בעיות המטרה.
נתונות טענות אודות יחסים בין המשתנים: מהירות, זמן, דרך. על התלמידים להבחין מתי מתקיים יחס ישר או יחס הפוך ולהשוות בין היחסים השונים.
התלמידים מתבקשים לקבוע נכונות הטענות הנתונות ולנמק. הנימוק יכול להיות על ידי הבאת דוגמה נגדית במקרה שהטענה שגויה או על ידי שימוש בנוסחה \((s=v\cdot t)\) כדי להוכיח נכונות של טענה.
מומלץ לערוך דיון אודות תפקידן של דוגמאות בכלל ובפרט תפקיד הדוגמה הנגדית להפרכת טענות.
(ניתן ללחוץ על התמונה ולהגדיל אותה במידת הצורך)
מקור: http://www.files.org.il/BRPortalStorage/a/3/94/68/92-4Ra2ko0kwS.pdf
הצעה לשאלות נוספות
על התלמידים להעלות שאלות נוספות שלא נשאלו באשכול למשל:
- מצאו בטבלה לפחות שתי דוגמאות לזמני הריצה של בן ושל בת שיש להם מהירויות שוות (בקירוב).
הסבירו את בחירתכם. - בדקו את נכונות הטענה: רונית רצה 1500 מטרים בזמן של 8:06 דקות. כדי לקבל אותו ציון רן לעבור את המסלול שלו (2000 מטרים) בזמן 8:28.
- מצאו בטבלה לפחות שתי דוגמאות לזמני הריצה של בן (2000 מטרים) ובת (1500 מטרים) שיש להם אותה מהירות (בקירוב). הסבירו את בחירתכם.
מהי המהירות ואיזה ציון קיבל כל אחד מהם?