אשכול מד טמפרטורה של מנגל - חלק ב - למורה
הנחיות למורה
יחידה
מדעים
כיתה מומלצת
כיתה ח / כיתה ט
משך הזמן המומלץ
30-45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקשר)
המרה של יחידות מדידה של טמפרטורה (צלזיוס, פרנהייט) – פיזיקה
מטרות האשכול
- הכרה של יחידות שונות למדידת טמפרטורה.
- פיתוח ההבנה שישנם מדי טמפרטורה שונים, המותאמים לצרכים שונים, וברמת דיוק שונה (מד טמפרטורה של מנגל, מד טמפרטורה למדידת טמפרטורה של בני אדם).
- פיתוח הידע של הקשר הלינארי הקיים בין מעלות צלזיוס למעלות פרנהייט ופיתוח המיומנות של המרת מעלות צלזיוס לפרנהייט ולהפך.
- פיתוח הידע מה זו שגיאה יחסית וכיצד ניתן לחשב אותה.
ידע מתמטי ומיומנויות מתמטיים נלמדים (חדשים)
| נושא | מושגים | מיומנויות |
|---|---|---|
| ייצוג תופעות באמצעות פונקציה קווית | – נוסחה | – הצבה |
| אחוז | – יחס – אחוז – שגיאה יחסית | – הבנת הסבר מילולי למושג "שגיאה יחסית". – חישוב שגיאה יחסית. |
| בעיות אורייניות מתוך מציאות הקרובה לתלמידים | – טמפרטורה – מעלות צלזיוס – מעלות פרנהייט – אחוז – יחס – המושג: שגיאה יחסית | – פתרון בעיות המשלבות בין הבנת טקסט מילולי והצגת נתונים, הלקוחים מתוך המציאות, לביצוע החישובים, המתאימים לפתרון הבעיות. – קריאת נתונים מתוך תמונה של מד טמפרטורה של מנגל. |
מערך דידקטי מומלץ:
- בפתיחת השיעור –שאלת שאלות לגבי אשכול א. כמו:
- באילו סולמות למדנו שניתן למדוד טמפרטורה?
- כיצד ממירים טמפרטורה ממעלות צלזיוס למעלות פרנהייט?
- מהו מד טמפרטורה מנגל ?
- מה ראינו לגבי מד טמפרטורה מנגל שהוצג בחלק א של האשכול?
- ארגון הכיתה: למידה בזוגות.
- ציוד נחוץ: מחשבון, מחשב, כדי שניתן יהיה להפעיל את היישומונים (לא הכרחי).
- ניהול השיעור: המורה יאפשר לתלמידים לענות על השאלות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות וביישומונים. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות.
- המורה יבקש, מתלמידים שסיימו לענות על השאלות באשכול, להציע שאלה נוספת הקשורה לאשכול ולפתור אותה.
- דיון בכיתה:
ניתן לקיים דיון קצר בכיתה לאחר המענה על בעיית מטרה 2 מאשכול א, ולאחר שתלמידים ענו על כל הבעיות באשכול. בדיונים אלו התלמידים יציגו ויסבירו את תשובותיהם. רצוי לאפשר להם להציג דרכים שונות לפתרון. - לסיכום הדיון, התלמידים יציגו את השאלות הנוספות שחשבו עליהן ואת הפתרונות לשאלות.
אשכול מד טמפרטורה של מנגל – חלק ב
תיאור סיטואציה
בחלק א' מצאנו כי נוסחת ההמרה ממעלות צלזיוס למעלות פרנהייט, על פי מד הטמפרטורה של המנגל שבתמונה 1, היא:
yF=2011xC+27311
ומצאנו כי נוסחת ההמרה המדויקת ממעלות צלזיוס למעלות פרנהייט היא:
yF=1.8xC+32
אבא של חנן הסביר לו שמד הטמפרטורה של המנגל מתאים למדידת טמפרטורות גבוהות ולא נדרש להיות כל כך מדויק, להבדיל ממד טמפרטורה המתאים לבני אדם.
לכן הנתונים במד הטמפרטורה של המנגל אינם מתאימים למציאת נוסחה מדויקת להמרה ממעלות צלזיוס לפרנהייט ולהפך.
תמונה 1

1. בעיית מטרה 1
חנן רצה לבדוק את רמת הדיוק בהמרה ממעלות צלזיוס למעלות פרנהייט שמוצגת במד הטמפרטורה של המנגל. אביו הסביר לו שלשם כך אפשר לחשב את השגיאה היחסית והסביר לו מושג זה.
לפניכם ההסבר שנתן אבא של חנן:
שגיאה יחסית היא ההפרש בין הגודל המקורב והגודל האמיתי, ביחס לגודל האמיתי. נהוג לבטא שגיאה יחסית באחוזים.
- מצאו מה היא השגיאה היחסית בהמרה למעלות פרנהייט, לפי מד הטמפרטורה של המנגל בתמונה 1, במקרה של 40∘C. בטאו תשובתכם באחוזים. פרטו חישוביכם.
- מצאו מה היא השגיאה היחסית בהמרה למעלות פרנהייט, לפי מד הטמפרטורה של המנגל בתמונה 1, במקרה של 315∘C. בטאו תשובתכם באחוזים. פרטו חישוביכם.
- אילו מסקנות ניתן להסיק לגבי השגיאה היחסית, בהמרה ממעלות צלזיוס למעלות פרנהייט, לפי מד הטמפרטורה של המנגל בתמונה 1? נמקו תשובתכם.
תוכלו להיעזר ביישומון לבדיקת תשובותיכם.
- אחרי שפתרתם את השאלות בבעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- הציבו ערכים בתיבה לצרכי המרה.
יישומון – מחשבון המרה לשבר פשוט
- ניתן לרשום מספר עשרוני, או תרגיל, ובסיום להקיש Enter.
פתרון לבעיית מטרה 1
- שגיאה יחסית: 100−104104⋅100=−3.846%
- שגיאה יחסית:600−599599⋅100=0.167%
- מסקנות אפשריות:
- השגיאה היחסית אינה קבועה.
- השגיאה היחסית יכולה להיות שלילית ויכולה להיות חיובית.
- יתכן שהשגיאה היחסית תהיה אפס: 1.8x+32=2011x+27311
- עבור 260∘C השגיאה היחסית היא אפס.
- (למתקדמים) אפשר להגיע לביטוי של השגיאה היחסית:
2011x+27311−1.8x−321.8x+32⋅100
ואפשר להמשיך ולשאול אותם: עבור כמה מעלות צלזיוס לא נוכל לחשב את השגיאה היחסית.
שגיאה יחסית היא ההפרש בין הגודל המקורב והגודל האמיתי, ביחס לגודל האמיתי.
נהוג לבטא שגיאה יחסית באחוזים.
בעיה 1.1.1
מלאו את הטבלה הבאה:
| מעלות צלזיוס | מעלות פרנהייט לפי מד הטמפרטורה של המנגל (גודל מקורב) | מעלות פרנהייט לפי ההגדרה באינטרנט (גודל אמיתי) | שגיאה יחסית באחוזים |
|---|---|---|---|
| 95∘C | |||
| 370∘C |
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- הציבו ערכים בתיבה לצרכי המרה.
יישומון – מחשבון המרה לשבר פשוט
- ניתן לרשום מספר עשרוני, או תרגיל, ובסיום להקיש Enter.
פתרון למדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
| מעלות צלזיוס | מעלות פרנהייט לפי מד הטמפרטורה של המנגל (גודל מקורב) | מעלות פרנהייט לפי ההגדרה באינטרנט (גודל אמיתי) | שגיאה יחסית באחוזים |
|---|---|---|---|
| 95∘C | 200∘F | 203∘F | 200−203203⋅100=−1.478% |
| 370∘C | 700∘F | 698∘F | 700−698698⋅100=0.287% |
מטרות מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
- עזרה במעבר מהסבר מילולי לחישוב של שגיאה יחסית, בהמרה מצלזיוס לפרנהייט, על פי מד הטמפרטורה של המנגל.
- תרגול בחישוב השגיאה היחסית על פי ההסבר הנתון.
שגיאה יחסית היא ההפרש בין הגודל המקורב והגודל האמיתי, ביחס לגודל האמיתי.
נהוג לבטא שגיאה יחסית באחוזים.
בעיה 1.2.1
מלאו את הטבלה הבאה:
| מעלות צלזיוס | מעלות פרנהייט לפי מד הטמפרטורה של המנגל (גודל מקורב) | מעלות פרנהייט לפי ההגדרה באינטרנט (גודל אמיתי) | היחס בין ההפרש שבין הגודל המקורב והגודל האמיתי, לבין הגודל האמיתי | שגיאה יחסית באחוזים |
|---|---|---|---|---|
| 95∘C | ||||
| 370∘C |
תוכלו להיעזר ביישומון המצורף.
- הציבו ערכים בתיבה לצרכי המרה.
יישומון – מחשבון המרה לשבר פשוט
- ניתן לרשום מספר עשרוני, או תרגיל, ובסיום להקיש Enter.
בעיה 1.2.2
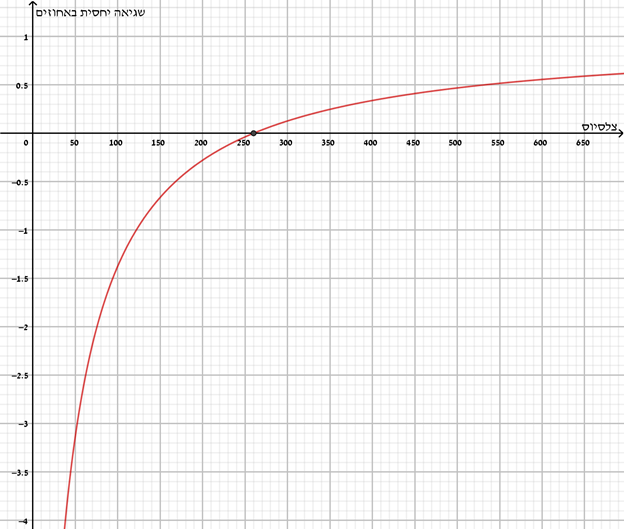
לפניכם הגרף של שגיאה יחסית באחוזים, בהמרה מצלזיוס לפרנהייט, לפי מד הטמפרטורה של המנגל שבתמונה 1.
- בדקו את תשובותיכם לבעיה 1.2.1 בעזרת הגרף (הנתון למטה) או בעזרת היישומון המצורף.
- האם יתכן שהשגיאה היחסית, בהמרה ממעלות צלזיוס למעלות פרנהייט, לפי מד הטמפרטורה של המנגל הנתון, תהיה שווה לאפס?
אם לא – נמקו.
אם כן – עבור איזו טמפרטורה, במעלות צלזיוס, השגיאה היחסית היא אפס?
ניתן להיעזר ביישומון המצורף.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- סמנו שיעורי נקודות בתיבות המתאימות בישומון ובדקו:
- לסימון נקודה: סמנו את תוכן הסוגריים בעזרת העכבר. רשמו: את שיעור x, פסיק, ואת שיעור y. לחצו Enter. שיעורי הנקודה צריכים להיות מוקפים בסוגריים.
- גררו את סמל ה +, שעל הקו האנכי המקווקו, כדי לצפות בערכים על הגרף המוצג.
- למתיחת או כיווץ הצירים, יש לבחור בתפריט העליון את ארבעת החיצים
 ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ
ולגרור את העכבר על הציר המבוקש. בסיום, כדי להמשיך, יש לבחור בחץ  בצד שמאל שבתפריט העליון.
בצד שמאל שבתפריט העליון. - להגדלה/להקטנה של הגרף, יש ללחוץ בעכבר על היישומון, ואז לגלגל את גלגלת העכבר כדי להגדיל/להקטין.
- לניקוי הישומון כדי להתחיל מחדש, יש ללחוץ על חיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.
(ניתן ללחוץ על הקישור ליישומון ולפתוח אותו בחלון נפרד).
פתרון למדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
| מעלות צלזיוס | מעלות פרנהייט לפי מד הטמפרטורה של המנגל (גודל מקורב) | מעלות פרנהייט לפי ההגדרה באינטרנט (גודל אמיתי) | היחס בין ההפרש שבין הגודל המקורב והגודל האמיתי, לבין הגודל האמיתי | שגיאה יחסית באחוזים |
|---|---|---|---|---|
| 95∘C | 200∘F | 203∘F | 200−203203 | 200−203203⋅100=−1.478% |
| 370∘C | 700∘F | 698∘F | 700−698698 | 700−698698⋅100=0.287% |
בעיה 1.2.2
מהגרף ניתן לראות כי שבערך עבור 260∘C, השגיאה היחסית שווה לאפס.
מטרות מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
- עזרה במעבר מהסבר מילולי לחישוב של השגיאה היחסית בהמרה, מצלזיוס לפרנהייט, על פי מד הטמפרטורה של המנגל (טבלה מפורטת יותר מאשר במדרגה 1).
- תרגול בחישוב השגיאה היחסית על פי ההסבר הנתון.
בעיה 1.2.2
- אפשרות לבדיקת התשובות בעזרת הגרף הנתון של שגיאה יחסית.
- הגרף הנתון יכול לעזור להסיק מסקנות לגבי השגיאה היחסית, בהמרה מצלזיוס לפרנהייט, לפי מד הטמפרטורה של המנגל הנתון בשאלה.