אשכול פרספקטיבה – חלק ג – עמודי תאורה במרחקים שווים
2.3. מדרגה 3 לבעיית המטרה
בצד שמאל מופיעים הסברי האומן לציור.
- מהו סוג המרובע CDEF שנוצר בין שני עמודי התאורה הראשונים, כאשר האומן מצייר אותם בפרספקטיבה חד-מגוזית?
נמקו.
- האומן צייר את העמוד השלישי בהתבסס על שיקולים גיאומטריים וטען שהציור שלו מתאים למציאות.
לפניכם כמה שיקולים גיאומטריים שהפעיל.
הסבירו את השקולים והשלימו את ההוכחה.
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית המטרה.
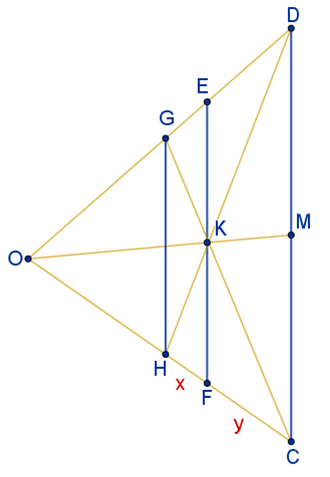
בסרטוט: HFFC=xy
במציאות: HF=FC ⟺ x=y
רציתי לצייר את העמוד השלישי במקום כזה, כך שיתקיים:
אם: x=y
אז: CD=EF=GH
גיליתי שזה מתקיים כאשר העמוד השני (כלומר EF) ממוקם בנקודת החיתוך של אלכסוני המרובע HGDC
KEGH=KFGH=xx+y
EFGH=2yx+y
אם: x=y
אז: EFGH=1
⇓
EF=CD
כלומר המרובע CDEF הוא מלבן
וזה תואם את המציאות!