אשכול דמיון בעדשות חלק ג - זכוכית מגדלת - למורה
הנחיות למורה
אשכול 3 מתוך 3 אשכולות.
יחידה:
מדע – אופטיקה
כיתה מומלצת:
כיתה ח / כיתה ט / כיתה י
משך הזמן המומלץ:
45-90 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
- עדשה מרכזת, מוקד עדשה, מהלך קרני אור העוברים דרך עדשה מרכזת, דמות אופטית וסרטוטה, דמות ממשיתף דמות לא ממשית, זכוכית מגדלת.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| דמיון משולשים | – משולשים דומים – יחס בין צלעות משולשים – פרופורציה | – זיהוי משולשים דומים שבהם לכל זווית במשולש אחד, יש זווית ששווה לה במשולש אחר. – מציאת יחס בין צלעות מתאימות במשולשים דומים. – מציאת נתונים חסרים מתוך תכונות הדמיון ותוך שימוש בפרופורציה. |
| הכללה של ביטויים מספריים | – הכללה – חוקיות – סדר גודל | – מציאת חוקיות בשילוב שברים ותכנים גאומטריים. |
| בעיות אורייניות מתוך מציאות קרובה לתלמידים | – עדשה מרכזת – מוקד – דמות אופטית | – פתרון בעיות המשלבות בין הבנת טקסט מילולי, המסביר את מהלך קרני האור העובר דרך עדשה מרכזת, לבין הידע המתמטי של תלמידים, בנושא דמיון משולשים. |
מטרת האשכול:
ידע מתמטי של דמיון משולשים, מאפשר להבין במה תלוי היחס בין גודל העצם לגודל הדמות של העצם, המשתקפת דרך עדשה מרכזת, ולחשב יחס זה.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
העמקה בנושא דמיון משולשים.
שלב הלמידה המומלץ:
בכיתה ח – סיכום של נושא דמיון משולשים.
בכיתה ט – לקראת סוף השנה, כחזרה וכהכנה לכיתה י'.
מערך דידקטי מומלץ:
ארגון הכיתה:
- ניתן לפתוח את השיעור בשאלות לגבי מה שנלמד באשכול "דמיון בעדשות – חלק א".
- ניתן להביא לכתה זכוכיות מגדלת ולעורר את השאלה מדוע דרך זכוכית מגדלת הדמות היא ישרה ומוגדלת.
- ארגון הכיתה בקבוצות של 2-4 תלמידים.
- התלמידים יקראו את תיאור הסיטואציה.
- דיון כיתתי קצר המבהיר את המושגים, ואת מהלך סרטוט דמות אופטית, לא ממשית, של עצם המשתקפת דרך עדשה מרכזת דקה.
- התלמידים פותרים את בעיית מטרה 1, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול.
דיון כיתתי בו התלמידים מציגים את תשובותיהם ומסבירים אותן. - התלמידים פותרים את בעיית מטרה 2 – סיכום.
דיון כיתתי בו התלמידים מציגים את תשובותיהם ומסבירים אותן. - התלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
שאלות מומלצות לדיון כיתתי:
- מה במבנה הבעיה עוזר כדי להגיע להכללה?
- כיצד נעזרתם ביישומון בפתרון הבעיות?
- במה עוזרת לנו המתמטיקה כדי להבין את המציאות, בהקשר לאשכול זה?
אשכול דמיון בעדשות חלק ג – זכוכית מגדלת
תזכורת
באשכולות הקודמים "דמיון בעדשות – חלק א" ו"דמיון בעדשות – חלק ב", למדנו:
- על עדשה דו-קמורה
- על שני מוקדי העדשה (\(F_1\) ו-\(F\)) המקיימים ש: \(OF=OF_1=f\)
- על מהלך קרני האור העוברות דרך עדשה קמורה, כאשר \((AO>f)\).
- אם מרחק העצם ממרכז העדשה, גדול ממרחק המוקד ממרכז העדשה \((AO>f)\), אז מתקבלת דמות ממשית (שניתן לראותה על מסך) והפוכה. גודלה של הדמות משתנה, בהתאם למרחק העצם ממרכז העדשה.
תיאור סיטואציה
זכוכית מגדלת היא עדשה קמורה, כפי שרואים בתמונה המצורפת.
הדמות המתקבלת היא ישרה ומוגדלת.
טלסקופ הוא מכשיר לצפייה בעצמים רחוקים.
בצורתו הפשוטה ביותר, הטלסקופ הוא צינור, שבכל אחד מקצותיו עדשה קמורה (מרכזת), המגדילה את העצם.
מיקרוסקופ הוא מכשיר אופטי המכיל עדשה אחת או יותר, ויוצר תמונה מוגדלת של עצם המונח על המשטח מול העדשות.
באילו תנאים מתקבלת דמות אופטית ישרה ומוגדלת, ובמה תלוי היחס בין גודל העצם לגודל הדמות?
סרטוט הדמות האופטית של עצם כאשר העצם נמצא בין מרכז העדשה \(O\) למוקד של העדשה \(F\) \((0<AO<f)\)
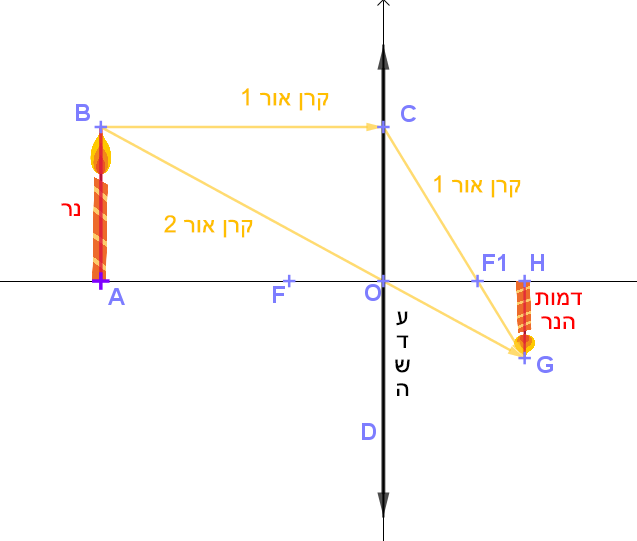
כפי שרואים בסרטוט המצורף, הקרניים היוצאות מראש העצם (\(B\)), לאחר שהן עוברות דרך העדשה הקמורה אינן נפגשות.
הדמות האופטית שמתקבלת, היא תוצאה של מפגש של המשכי הקרניים לאחר שעברו דרך העדשה הקמורה:
(המשכי הקרניים מסומנות על ידי קו מרוסק)
המשך הקרן \(DF_1\) עובר דרך נקודה \(G\).
המשך הקרן \(BO\) עובר דרך הנקודה \(G\).
דמות אופטית המתקבלת כתוצאה ממפגש המשכי הקרניים, היא דמות שאינה ממשית. דמות כזו ניתן לראות בעין, אך לא ניתן לראות על מסך.
הדמות בסרטוט שלפנינו היא מוגדלת וישרה.
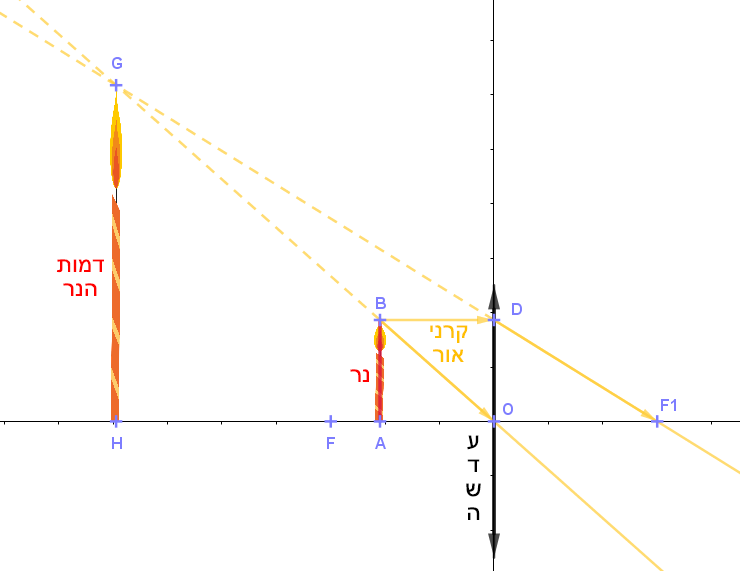
1. בעיית מטרה 1
נתון כי:
הנר \((AB)\) מאונך לציר עדשה \((HF_1)\)
דמות הנר \((HG)\) מאונכת לציר העדשה.
קרן האור \((BD)\) מקבילה לציר העדשה.
מרחק המוקד ממרכז העדשה הוא 3 ס"מ,
מרחק הנר ממרכז העדשה הוא 2 ס"מ.
- חשבו את המרחק של דמות הנר ממרכז העדשה.
\(\space\) - פי כמה גדולה דמות הנר מהנר?
\(\space\) - פי כמה גדולה דמות הנר מהנר כאשר \(AO=מ"ס \space0.75\)?
\(\space\) - אם דמות הנר גדולה פי 2 מהנר, מהו מרחק
הנר ממרכז העדשה?
בכל אחד מהסעיפים תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2 – סיכום.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון בעיית מטרה 1
פתרון לסעיפים א + ב
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(OF=OF_1=מ"ס\space\space 3\)
\(AO=מ"ס\space\space 2\)
\(\Large\frac{AB}{HG}\normalsize=3\)
יש לחשב את: \(HO\space ,\space \Large\frac{AB}{HG}\)
פתרון:
סעיף א
\(\triangle {DOF_1}\sim\triangle{GHF_1}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{DO}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\)
מרובע ABDO הוא מלבן
(או חפיפת משולשים BDO ו- OAB)
\(\Downarrow\hspace{1cm}\)
\(DO=AB\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{3}{HO+3}\)
\(\Downarrow\hspace{1cm}\)
\(\triangle {BAO}\sim\triangle{GHO}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
(המשך פתרון סעיף א)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{HO}\normalsize=\Large\frac{2}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{3}{HO+3}\normalsize=\Large\frac{2}{HO}\)
\(\Downarrow\hspace{1cm}\)
\(3\cdot HO=2\cdot HO+6\)
\(\Downarrow\hspace{1cm}\)
\(HO=מ"ס\space6\)
סעיף ב
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{2}{6}\normalsize=\Large\frac{1}{3}\)
דמות הנר גדולה פי 3 מהנר.
סעיף ג
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(OF=OF_1=מ"ס\space\space 3\)
\(AO=מ"ס\space\space 0.75\)
יש לחשב את: \(\Large\frac{AB}{HG}\)
פתרון:
נציב בפתרון סעיף א:
\(AO=מ"ס\space\space 0.75\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{0.75}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{3}{HO+3}\normalsize=\Large\frac{0.75}{HO}\)
\(\Downarrow\hspace{1cm}\)
\(3 \cdot HO=0.75\cdot HO+2.25\)
\(\Downarrow\hspace{1cm}\)
(המשך פתרון סעיף ג)
\(\Downarrow\hspace{1cm}\)
\(HO=מ"ס\space\space 1\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{0.75}{1}\normalsize=\Large\frac{3}{4}\)
דמות הנר גדולה פי \(\Large\frac{4}{3}\) מהנר.
סעיף ד
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(OF=OF_1=מ"ס\space\space 3\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{1}{2}\)
יש לחשב את: \(AO\)
פתרון:
נציב בפתרון סעיף א:
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{1}{2}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{3}{HO+3}\normalsize=\Large\frac{1}{2}\)
\(\Downarrow\hspace{1cm}\)
\(HO=מ"ס\space\space 3\)
\(\Downarrow\hspace{1cm}\)
(המשך פתרון סעיף ד)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{1}{2}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{OA}{3}\)
\(\Downarrow\hspace{1cm}\)
\(AO=מ"ס\space\space 1.5\)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(OF=OF_1=מ"ס\space\space 3\)
\(AB=מ"ס\space\space 4\)
\(HG=מ"ס\space\space 12\)
יש לחשב את: \(HF_1\space ,\space HO\)
פתרון:
\(\triangle {DOF_1}\sim\triangle{GHF_1}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{DO}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\)
מרובע ABDO הוא מלבן
(או חפיפת משולשים BDO ו- OAB)
\(\Downarrow\hspace{1cm}\)
\(DO=AB\)
\(\Downarrow\hspace{1cm}\)
(המשך פתרון)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{4}{12}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{3}{HF_1}\)
\(\Downarrow\hspace{1cm}\)
\(HF_1=מ"ס\space\space 9\)
\(HO=9-3=מ"ס\space\space 6\)
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
הסרטוט בבעיה שבמדרגה, זהה לזה שבבעיית המטרה. אך הבעיה במדרגה פשוטה יותר מבעיית המטרה, כיוון שנידרש בה להוכיח דמיון בין זוג אחד של משולשים. בעוד שכדי לפתור את בעיית המטרה, יש להוכיח דמיון בין שני זוגות של משולשים.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(AB=מ"ס\space\space 4\)
\(HG=מ"ס\space\space 10\)
\(AO=מ"ס\space\space 2\)
יש לחשב את: \(HA\)
פתרון:
\(\triangle {BAO}\sim\triangle{GHO}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{AB}{HG}\normalsize=\Large\frac{4}{10}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{2}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(OH=מ"ס\space\space 5\)
\(\Downarrow\hspace{1cm}\)
\(HA=OH-OA=5-2=מ"ס\space\space 3\)
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
הסרטוט בבעיה שבמדרגה 2, זהה לזה שבבעיית מדרגה 1 ובבעיית המטרה. אך הבעיה במדרגה 2, פשוטה יותר מבעיית המטרה ומהבעיה במדרגה 1, כיוון שעל פי הנתונים בבעיה זו, ניתן לזהות באופן ישיר בין אילו משולשים יש להוכיח דמיון.
2. בעיית מטרה 2 – סיכום
- מלאו את הטבלה הבאה בהתאם לנתונים ולחישובים בבעיית מטרה 1 והגיעו להכללה:
סעיף בבעיית מטרה 1 מרחק המוקד ממרכז העדשה (\(f\)) מרחק הנר ממרכז העדשה (\(AO\)) יחס: \(\Large\frac{AO}{f}\normalsize=k\) היחס בין גודל הנר לגודל דמות הנר \(\Large\frac{AB}{HG}\) סעיף ב 3 ס"מ 2 ס"מ סעיף ג 3 ס"מ 0.75 ס"מ סעיף ד 3 ס"מ \(\Large\frac{1}{2}\) הכללה \(f\) \(AO\)
\((0\lt AO\lt f)\)
\(\space\) - הסבירו מדוע כאשר מרחק הנר ממרכז העדשה, קטן ממרחק המוקד ממרכז העדשה \((0\lt AO\lt f)\), הדמות גדולה יותר מהעצם.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 2, המשיכו למה עוד אפשר לשאול.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון בעיית מטרה 2
סעיף א
| סעיף בבעיית מטרה 1 | מרחק המוקד ממרכז העדשה (\(f\)) | מרחק הנר ממרכז העדשה (\(AO\)) | יחס: \(\Large\frac{AO}{f}\normalsize=k\) | היחס בין גודל הנר לגודל דמות הנר \(\Large\frac{AB}{HG}\) |
|---|---|---|---|---|
| סעיף ב | 3 ס"מ | 2 ס"מ | \(\Large\frac{2}{3}\) | \(1-\Large\frac{2}{3}\normalsize=\Large\frac{1}{3}\) |
| סעיף ג | 3 ס"מ | 0.75 ס"מ | \(\Large\frac{1}{4}\) | \(1-\Large\frac{1}{4}\normalsize=\Large\frac{3}{4}\) |
| סעיף ד | 3 ס"מ | 1.5 ס"מ | \(\Large\frac{1}{2}\) | \(1-\Large\frac{1}{2}\normalsize=\Large\frac{1}{2}\) |
| הכללה \(\color{red}*\) | \(f\) | \(AO\) \((0\lt AO\lt f)\) | \(\Large\frac{AO}{f}\normalsize=k\) | \(1-\Large\frac{AO}{f}\normalsize=1-k\) |
סעיף ב
אם מרחק הנר ממרכז העדשה קטן ממרחק המוקד ממרכז העדשה אז \(0<\Large\frac{AO}{f}\normalsize=k<1\).
היחס בין גודל עצם לגודל הדמות שווה ל- \(1-k\).
עבור \(0<k<1\), קיים ש: \(0<1-k<1\). כלומר, גודל העצם קטן מגודל הדמות. ובמילים אחרות, הדמות גדולה מהעצם.
* הערה: יש לציין שההכללה אליה מגיעים על פי החוקיות המתגלה בטבלה, היא בגדר השערה, כיוון שהתלמיד לא נדרש להוכחה כללית.
תלמידים מתקדמים יכולים להגיע להוכחה כללית:
הוכחה כללית עם פרמטרים (סעיף א)
נתון כי: \(AB\perp HF_1\)
\(HG\perp HF_1\)
\(BD ∥ HF_1\)
\(OF=OF_1=f\)
\(AO=k\cdot f\)
יש לבטא את: \(HO\space\space ,\space\space \Large\frac{AB}{HG}\)
פתרון:
\(\triangle {DOF_1}\sim\triangle{GHF_1}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{DO}{HG}\normalsize=\Large\frac{OF_1}{HF_1}\)
מרובע ABDO הוא מלבן
(או חפיפת משולשים BDO ו- OAB)
\(\Downarrow\hspace{1cm}\)
\(DO=AB\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9 }{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OF_1}{HF_1}\normalsize=\Large\frac{f}{HO+f}\)
\(\triangle {BAO}\sim\triangle{GHO}\) על פי משפט דמיון ז.ז.
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9}{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{k\cdot f}{OH}\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9 }{\Large\frac{AB}{HG}}\normalsize=\Large\frac{f}{HO+f}\normalsize=\Large\frac{k\cdot f}{HO}\)
(המשך פתרון)
\(\Downarrow\hspace{1cm}\)
\(\Large\frac{1}{HO+f}\normalsize=\Large\frac{k}{HO}\)
\(\Downarrow\hspace{1cm}\)
\(HO=k\cdot HO+k\cdot f\)
\(\Downarrow\hspace{1cm}\)
\((1-k)HO=k\cdot f\)
\(\Downarrow\hspace{1cm}\)
\(HO=\Large\frac{k\cdot f}{1-k}\)
\(\Downarrow\hspace{1cm}\)
\(\color{#3fabd9 }{\Large\frac{AB}{HG}}\normalsize=\Large\frac{OA}{OH}\normalsize=\Large\frac{k\cdot f}{\left (\Large\frac{k\cdot f}{1-k}\right )}\normalsize=1-k\)
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.