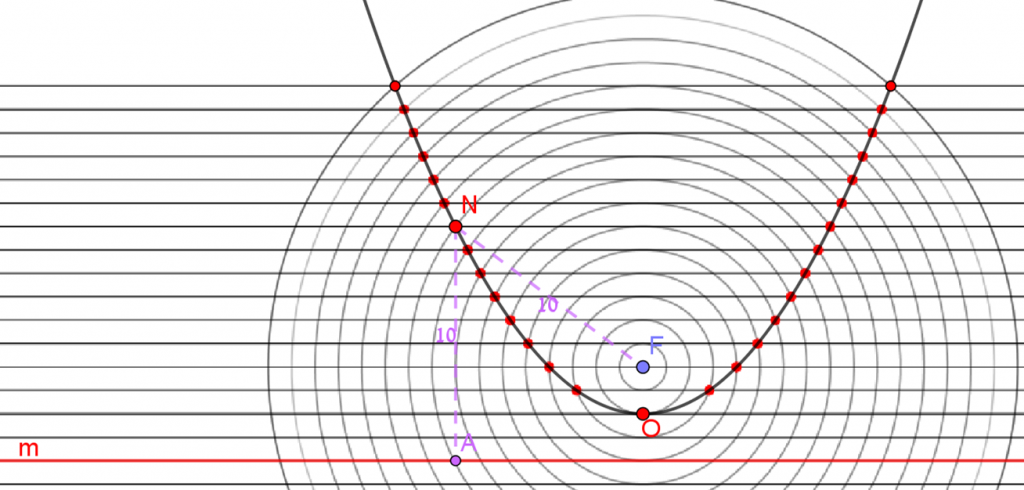
عنقود مرايا كقطوع مكافئة - بؤرة، دليل وما بينهما - جزء أ - مقدّمة
(يمكن الضغط على الرسم وتكبيرها)
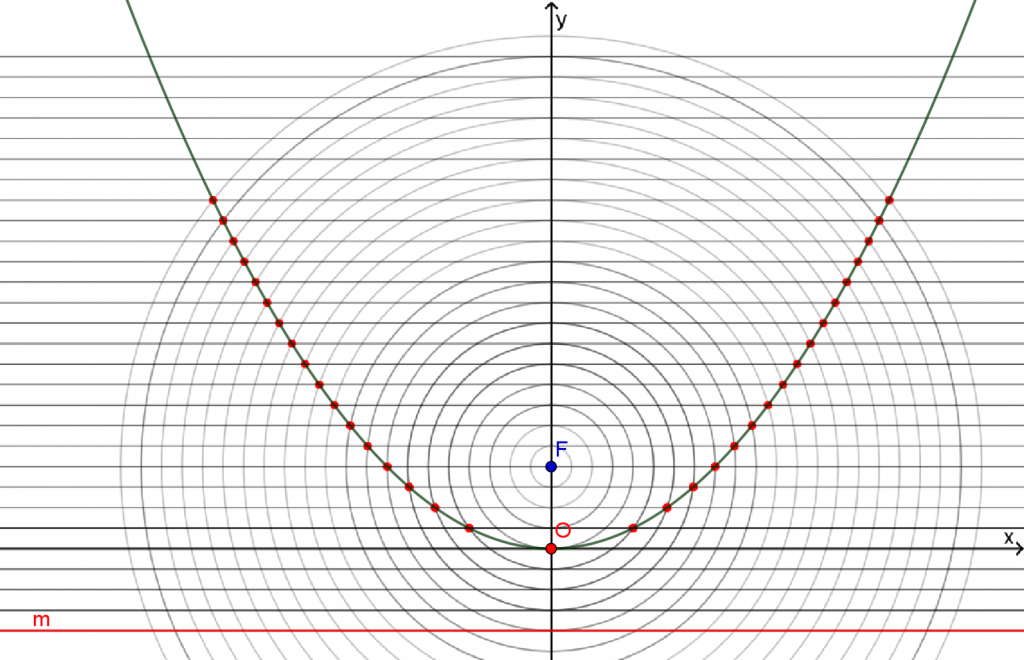
نُضيف هيئة محاور للرسم (לחצו על הכפתור “צירים” ביישומון)،
حيث يكون محور x موازيًا للمستقيم m ونقطة أصل المحورين في النقطة O (أقرب نقطة للمستقيم m وبُعدها عن النقطة F يساوي بُعدها عن المستقيم m):
(يمكن الضغط على الرسم وتكبيرها)
هذا هو قطع مكفئ (المعرف لنا) والذي تعبيره الجبري هو f(x)=ax2f(x)=ax2.
انظروا التطبيق المرفق.
- انتقلوا إلى مسألة هدف 2 – تلخيص (اختياري).
- أو انتقلوا إلى تتمة لتلخيص.
- يُمكن جرّ النقطة الموجودة على القطع المكافئ، كي نرى البُعد بين البؤرة (النقطة F) والدليل (الخط m).
- أنقروا على الزر “محاور” لإظهار / إخفاء هيئة المحاور.
- يمكن بالاستعانة بأشرطة الجرّ أن نعرض:
- رقم الدائرة.
- رقم الخط الافقي.
- ملاحظة: عندما تظهر الدوائر والخطوط الافقيّة، تظهر أيضًا نقاط التقاطع الملائمة بينها.
مبنى العنقود
- 1. مسألة هدف 1
- تلخيص
- 2. مسألة هدف 2 – تلخيص (اختياري)
- تتمة لتلخيص
- 3. ماذا يمكن أن نسأل أيضًا؟