عنقود مرايا كقطوع مكافئة - بؤرة، دليل وما بينهما - جزء أ - مقدّمة
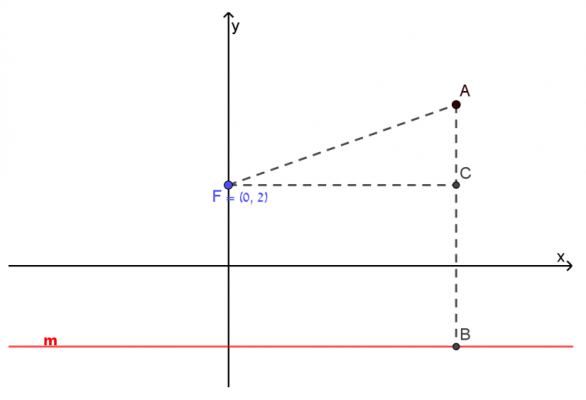
- عبّروا عن القطعتين AF و-AC بواسطة \(y_A\). علّلوا جوابكم.
\(\space\) - برهنًوا أن: \(y_A=\Large\frac{1}{8}\normalsize (x_A)^2\)
\(\space\) - جدوا إحداثيات ثلاث نقاط، بُعدا كل واحدة منها عن نقطة F وعن المستقيم m متساويان.
\(\space\) - أي خد بياني ينتج من مجموع كل النقاط التي تبعد عن النقطة F يساوي بُعدها عن المستقيم m؟
علّلوا جوابكم.
- إذا حليّتم مسألة التلخيص (اختياري), انتقلوا إلى تتمة لتلخيص.
مبنى العنقود
- 1. مسألة هدف 1
- تلخيص
- 2. مسألة هدف 2 – تلخيص (اختياري)
- تتمة لتلخيص
- 3. ماذا يمكن أن نسأل أيضًا؟