אשכול דמיון בעדשות חלק ב - הכללה
באשכול הקודם "דמיון בעדשות – חלק א", למדנו:
- מה זו עדשה דו קמורה
- על המוקדים בעדשה קמורה (F,F1)(F,F1),
ועל מרחק המוקדים ממרכז העדשה: OF=OF1=fOF=OF1=f - על מהלך קרני האור העוברות דרך עדשה קמורה
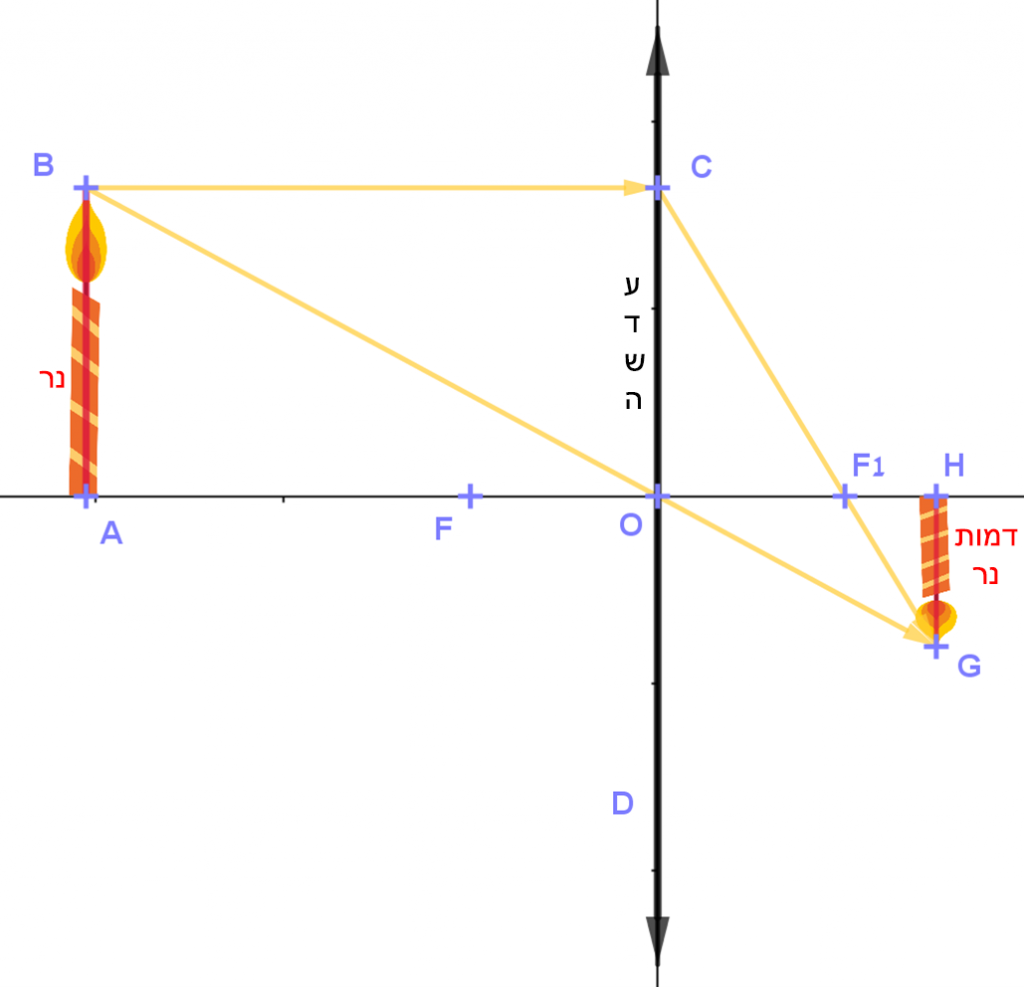
- על סרטוט הדמות האופטית של נר (HG) המשתקף דרך עדשה קמורה (ראו סרטוט מצורף)
- כאשר AO>fAO>f, הדמות האופטית היא ממשית והפוכה.
גודלה יכול להיות קטן מגודל מהנר, גדול מהנר או שווה לו.
באשכול זה נבדוק במה תלוי גודל הדמות האופטית, כאשר AO>fAO>f.
1. בעיית מטרה 1 – הכללה
באשכול "דמיון בעדשות – חלק א", הוכח כי כאשר AO>fAO>f, מתקיים ש:
ABHG=COHG=OF1HF1ABHG=COHG=OF1HF1
ABHG=AOOHABHG=AOOH
- היעזרו במה שהוכח והשלימו את הטבלה. נמקו תשובותיכם.
תוכלו להיעזר ביישומון המצורף.
מרחק המוקד ממרכז העדשה ff מרחק הנר ממרכז העדשה AOAO מרחק הדמות ממרכז העדשה HOHO AOf=kAOf=k היחס בין גודל הנר לגודל דמות הנר ABHGABHG 2 ס"מ 8 ס"מ 8/3 ס"מ 4 3 2 ס"מ 6 ס"מ חשבו חשבו חשבו 2 ס"מ 4 ס"מ 4 ס"מ 2 1 2 ס"מ 3 ס"מ 6 ס"מ 1.5 0.5 2 ס"מ 2.5 ס"מ חשבו חשבו חשבו הכללה ff AOAO ———— השלימו השלימו - הסיקו מסקנות מהטבלה, כאשר AO>fAO>f:
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר גדול יותר מאורך דמות הנר?
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר שווה בגודלו לאורך דמות הנר?
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר קטן יותר מאורך דמות הנר?
נמקו תשובותיכם.
תוכלו להיעזר ביישומון המצורף.
- מה ניתן להסיק לגבי הדמות כאשר k=1k=1?
סרטטו סרטוט מתאים והוכיחו תשובתכם בדרך גאומטרית.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.












