אשכול מראות פרבוליות - מוקד, מדריך ומה שביניהם - חלק ג - למורה
הנחיות למורה
אשכול 3 מתוך 3 אשכולות.
יחידה:
מדע – מתמטיקה
כיתה מומלצת:
כיתה ט / כיתה י
משך הזמן המומלץ:
45 דקות
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| פרבולה | – מוקד – מדריך – מרחק בין שתי נקודות – מרחק בין נקודה לישר | – יישום תכונה של פרבולה: כל נקודה על הפרבולה נמצאת במרחק שווה ממוקד הפרבולה ומהמדריך. |
| פרבולה | – ביטוי אלגברי של פרבולה. | – מציאת ביטוי אלגברי של פרבולה, על פי נקודה על הפרבולה וגרף הפרבולה. |
| משפט פיתגורס | – משולש ישר זווית – ניצב – יתר | – יישום המשפט במערכת צירים לצורך פתירת בעיה. |
מטרת האשכול:
יישום התכונה של הפרבולה: כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה. יישום תכונה זו הינו לצורך פתרון בעיה במציאות, הקשורה למראות פרבוליות.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
- מוקד של פרבולה
- מדריך של פרבולה
- כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה.
שלב הלמידה המומלץ:
לאחר הכרת הפרבולה ותכונותיה.
מערך דידקטי מומלץ:
ארגון הכיתה:
- חזרה במליאה על המושגים מוקד ומדריך ועל התכונה של פרבולה בהקשר זה, שנלמדו באשכול – חלק א. רצוי להיעזר ביישומון המצורף (חזרה).
- ארגון הכיתה בקבוצות של 2-4 תלמידים.
- תלמידים קוראים את "תיאור הסיטואציה".
- במליאה, הקרנת קטע הווידאו המצורף (בניית מראה פרבולית – YouTube) – בו ניתן לראות כיצד בונים מראה פרבולית על פי אותם עקרונות שנלמדו באשכול א. כמו-כן, גם מדגימים בווידאו את מהלך קרני האור כאשר הן פוגעות במראה פרבולית.
- דיון כיתתי קצר בו ניתן לבקש מהתלמידים להסביר מה רואים בווידאו.
- תלמידים פותרים את בעיית מטרה 1, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול וביישומונים.
- דיון כיתתי בו תלמידים מציגים את תשובותיהם ומסבירים אותן.
- תלמידים פותרים את בעיית מטרה 2 – סיכום.
- דיון כיתתי בו תלמידים מציגים את תשובותיהם ומסבירים אותן.
- תלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
שאלות מומלצות לדיון כיתתי:
- באילו קשיים נתקלתם בפתרון בעיית המטרה או בעיית הסיכום?
- כיצד עזרו המדרגות בהתמודדות עם הקשיים בהם נתקלתם?
- כיצד עזרו היישומונים בהתמודדות עם הקשיים בהם נתקלתם?
- אילו עוד שימושים אתם מכירים למראות פרבוליות? (למשל: הדלקת אש באמצעות קערה פרבולית – ראו קישור לווידאו ברשימת המקורות)
אשכול מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק ג
למדנו כי:
הגרף המתקבל מאוסף כל הנקודות, שמרחקן מנקודה F שווה למרחקן מישר m, הוא פרבולה:
נקודה F נקראת מוקד הפרבולה. ישר m נקרא מדריך הפרבולה.
לפרבולה המוכרת לנו, תכונה נוספת:
מרחקה של כל נקודה על הפרבולה, ממוקד הפרבולה, שווה למרחקה ממדריך הפרבולה.
ראו יישומון מצורף.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
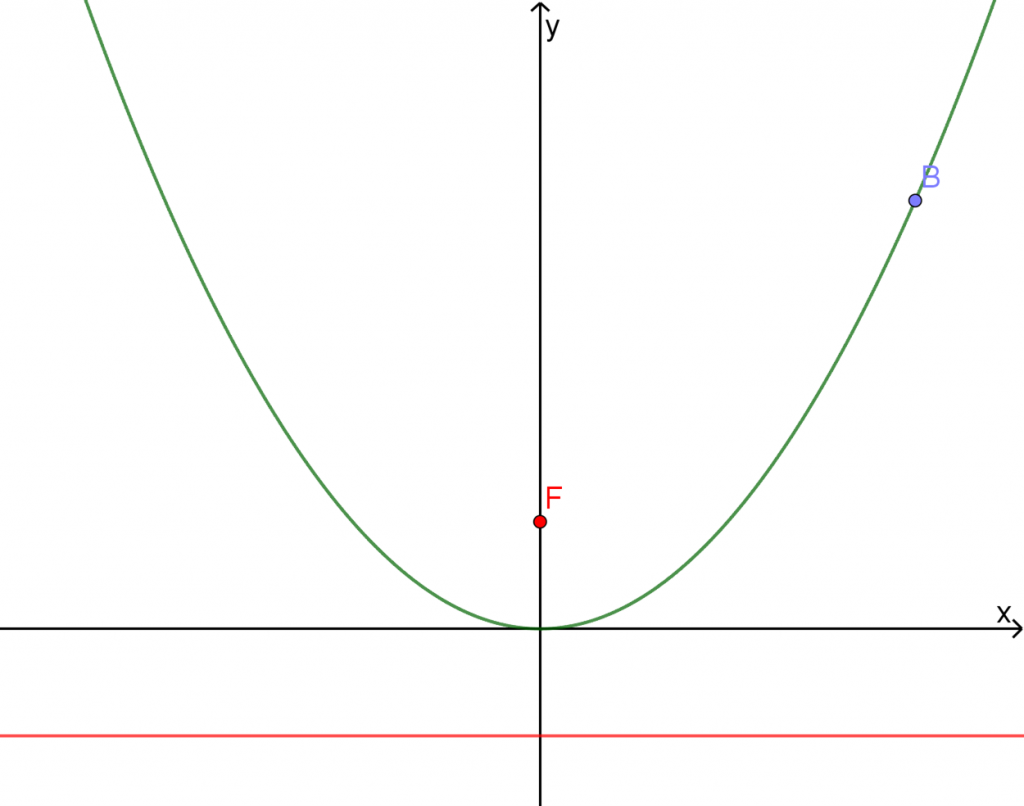
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.
תיאור סיטואציה
מראה היא הֶתְקן בעל משטח פנים המחזיר את קרני האור. המראה השטוחה הנפוצה עשויה זכוכית ועל פניה האחוריים מונחת שכבה דקה של מתכת כלשהי (לרוב כסף) כך שהנוף שמולה משתקף עליה.
מראה קעורה יכולה לרכז קרני אור מקבילות לנקודה אחת, או להפך, להפוך אור המגיע מנקודה אחת לקרניים מקבילות. אחד מהסוגים של מראות קעורות היא מראה שצורתה פרבולה.
במראה שצורתה פרבולה, קרן אור המגיעה מעצם מרוחק, במקביל לציר (ציר הסימטריה של הפרבולה) ופוגעת במראה, מוחזרת אל נקודה אחת. נקודה זו היא במפתיע המוקד של הפרבולה. נסמן אותה ב- F (כפי שלמדנו). לכן, כל קרני אור המגיעות מעצם מרוחק ופוגעות במראה שצורתה פרבולה, מתרכזות במוקד הפרבולה.
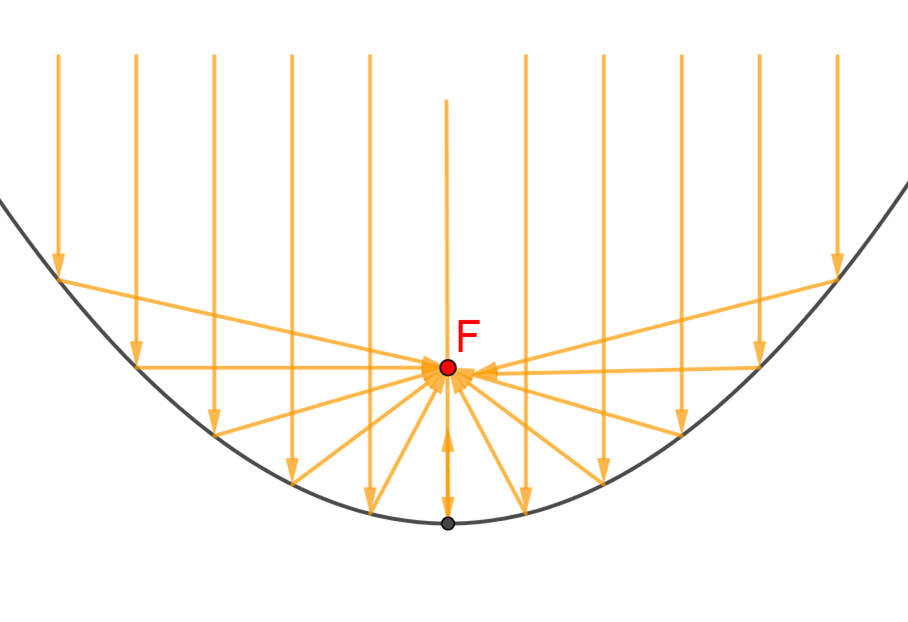
תכונה זו משמשת בקולט שמש ליצירת אנרגיה סולארית.
בתמונה שלפניכם, צלחת פרבולית לניצול אנרגיית השמש במרכז מחקר בשדה בוקר.
צורתה הפרבולית של הצלחת, מביאה להחזרת כל קרני השמש למוקד הפרבולה, ובכך יוצרת בו חום גבוה.
ולהפך, קרן אור המגיעה ממוקד הפרבולה ופוגעת במראה פרבולית מוחזרת, כך שהיא מקבילה לציר הסימטריה של הפרבולה.
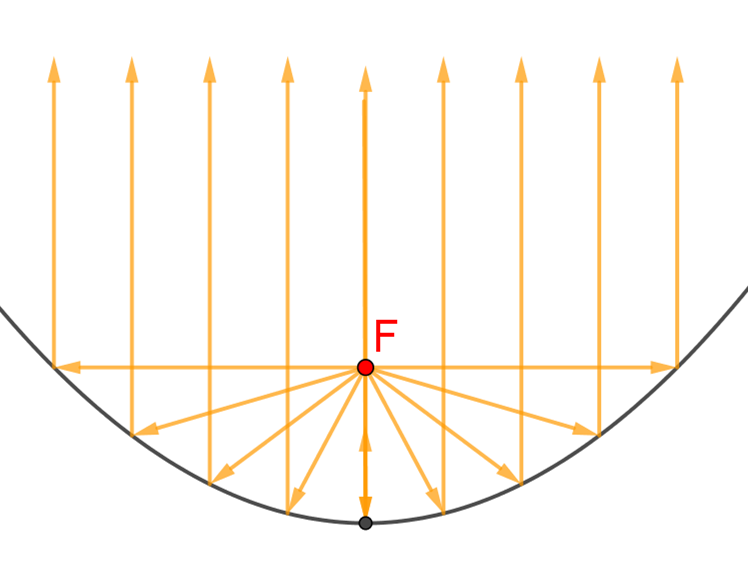
תכונה זו משמשת ליצירת אלומת אור שקרניה מקבילות.
לדוגמה: זרקור ופנסי מכוניות שבנויים בצורה של מראה פרבולית, מקור אור נמצא במוקד שלה.
צפו בווידאו המצורף.
בווידאו מראים כיצד בונים מראה פרבולית וממחישים את מהלך קרני האור המקבילות הפוגעות במראה הפרבולית.
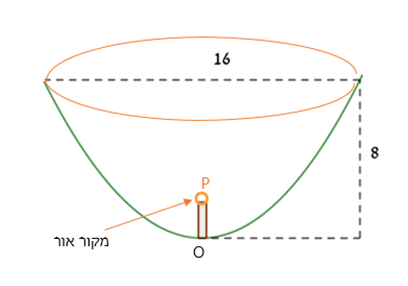
- חשבו היכן יש להתקין את מקור האור בפנס של המכונית. (חשבו את OP).
- מצאו את הביטוי האלגברי של הפרבולה.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2 – סיכום.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון בעיית מטרה 1
א. חישוב OP
את הנורה יש להתקין במוקד המראה הפרבולית. לכן, נקודה P היא מוקד הפרבולה.
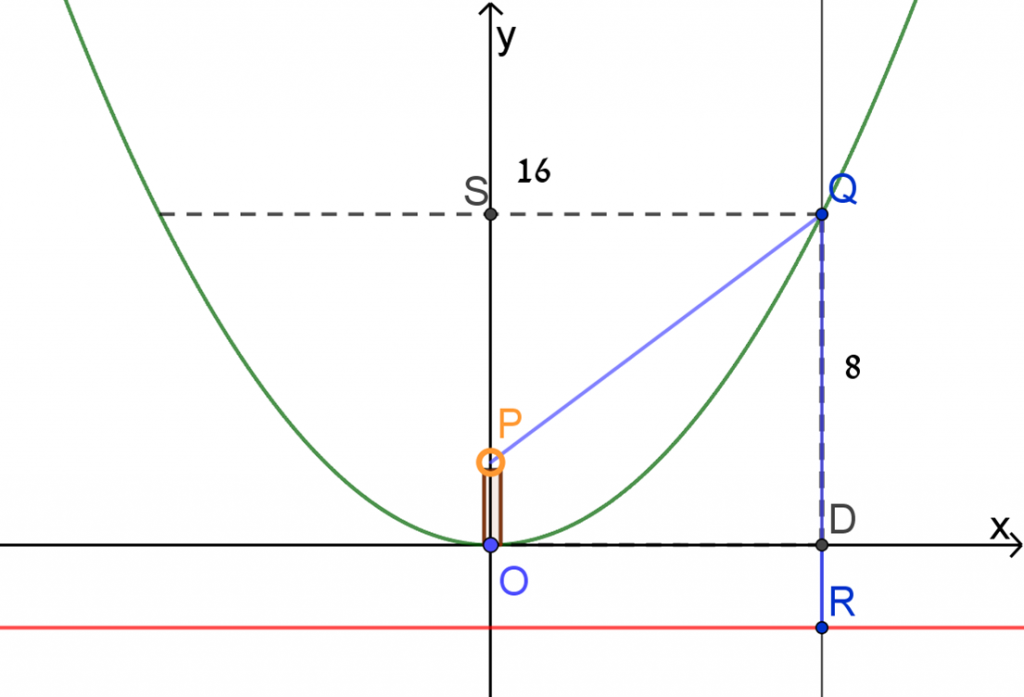
נוסיף לסרטוט מערכת צירים, כך שראשית הצירים תהיה בנקודה O.
\(\space\)
נמצא את שיעורי נקודה P.
\(Q(8,8)\)
נסמן \(P(0,t)\)
ישר m המדריך: \(y=-t\)
\(PQ=QR=8+t\)
\(SQ=8\)
\(SP=8-t\)
משפט פיתגורס במשולש PSQ – משולש ישר זווית
\(8^2+(8-t)^2=(8+t)^2\)
\(64+64-16t+t^2=64+16t+t^2\)
\(32t=64\)
\(t=2\)
\(OP= {מ"ס\space\space} 2\)
\(\space\)
ב. ביטוי אלגברי של הפרבולה:
\(8=a\cdot 64\)
\(y=\Large\frac{1}{8}\normalsize x^2\)
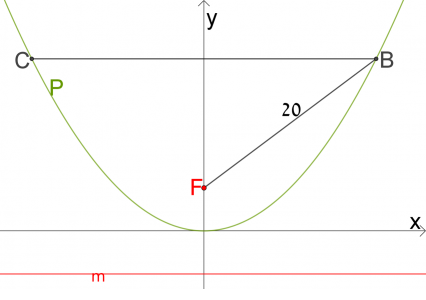
מצאו את:
- הביטוי האלגברי למדריך הפרבולה.
- שיעורי מוקד הפרבולה.
- אורך הקטע BC.
נמקו ופרטו חישוביכם.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
א. ביטוי אלגברי למדריך של הפרבולה:
\(FB=BA=20\)
\(AG=20-16=4\)
המדריך: \(y=-4\)
\(\space\)
ב. שיעורי מוקד הפרבולה
המוקד \(F(0,4)\)
\(\space\)
ג. אורך הקטע BC
\(EF=16-4=12\)
\(EB=\sqrt{20^2-12^2}=16\)
\(CB=\space ךרוא\space תודיחי\space32\)
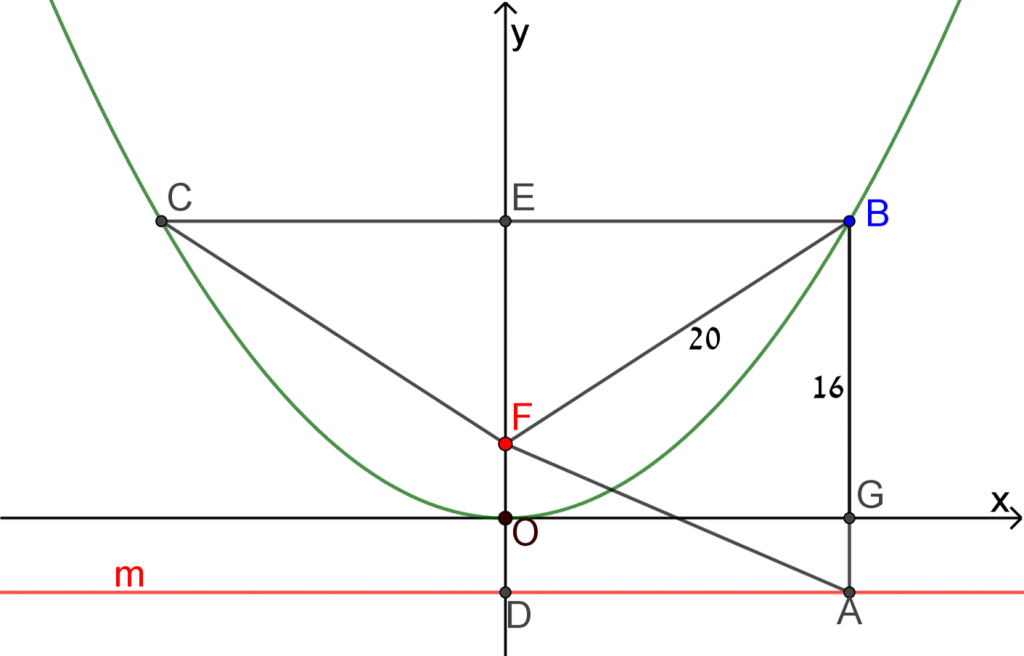
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
הבעיה דומה לבעיית המטרה.
בסרטוט המצורף לבעיית המדרגה מופיעה מערכת צירים. בבעיית המטרה יש להבין שצריך להוסיף לסרטוט מערכת צירים.
בבעיית המדרגה מתבקשים למצוא את הביטוי האלגברי למדריך הפרבולה.
לצורך פתרון בעיית המטרה, יש למצוא את הביטוי האלגברי למדריך, למרות שלא מתבקשים למצוא זאת במפורש.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
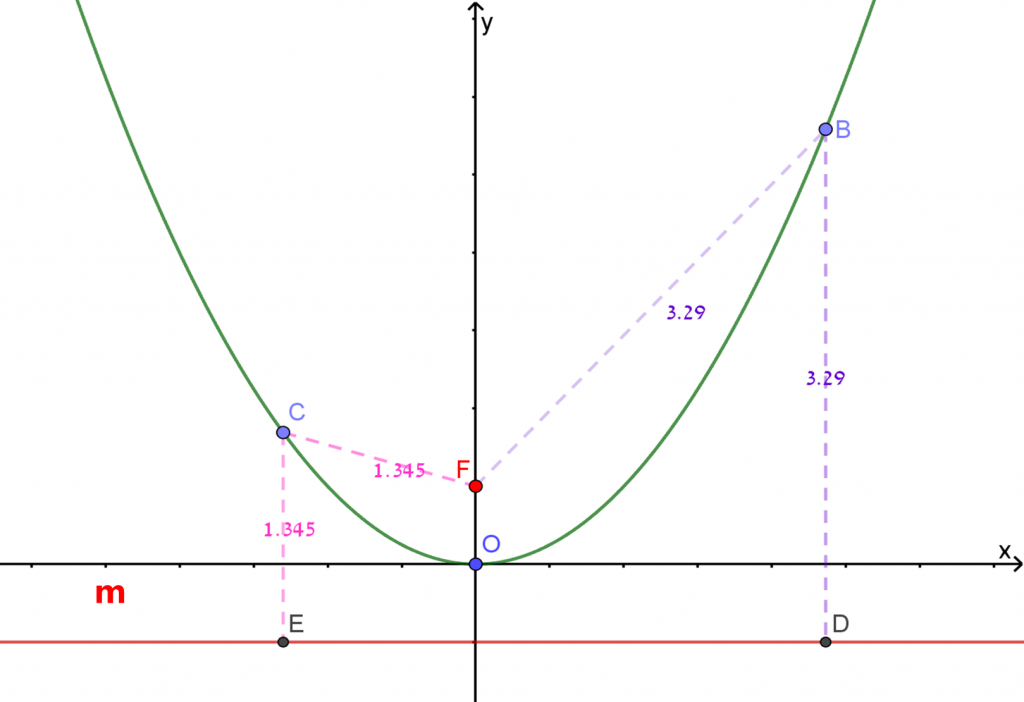
מצאו בסרטוט לפחות 5 זוגות של קטעים השווים באורכם.
נמקו תשובתכם.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- ניתן לגרור את נקודה B שעל הפרבולה.
- לחישוב אורכי קטעים, יש לרשום שמות קטעים בתיבות המתאימות, וללחוץ Enter.
- לחיצה על צבע, ואז על קטע, תצבע את הקטע – וזאת כדי להקל על זיהוי קטעים שווים.
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
קטעים שווים בסרטוט:
\(FG=BF\)
\(AB=BF\)
\(GF=AB\)
\(EB=GE\)
\(DO=FO\)
\(DA=EB\)
\(DA=GE\)
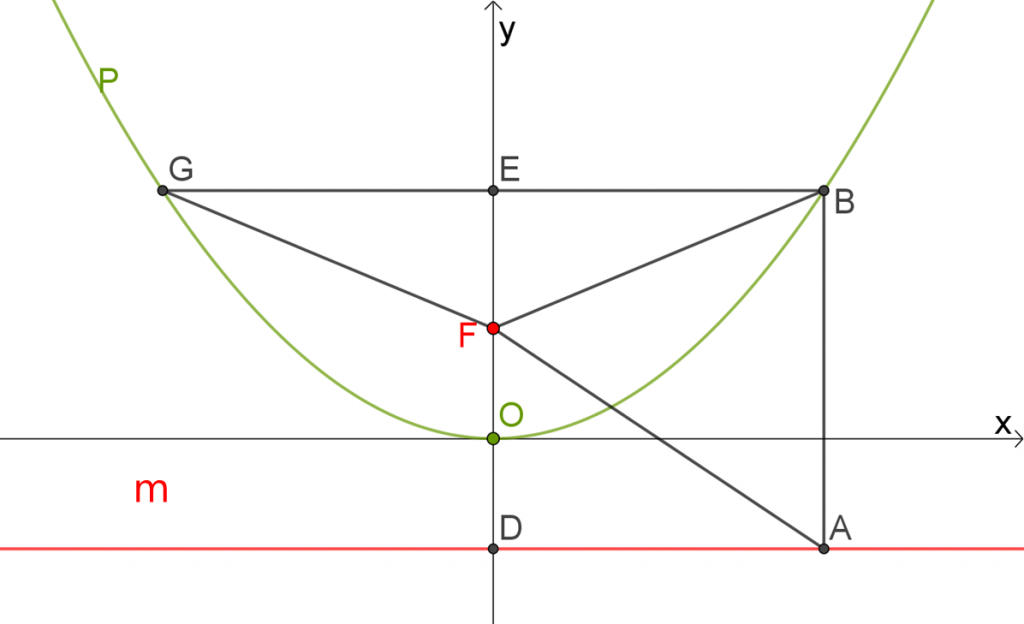
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
בבעיית המדרגה מתבקשים למצוא קטעים שווים בסרטוט. זאת כדי להדגיש את הסימטריות של הפרבולה ואת התכונה שכל נקודה על הפרבולה נמצאת במרחקים שווים ממדריך הפרבולה ומהמוקד שלה – תכונות שיש להיעזר בהן בפתרון בעיית המטרה.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
| ביטוי אלגברי של פרבולה | שיעורי נקודה \(B\) על הפרבולה | שיעורי המוקד \((F)\) |
|---|---|---|
| \(p(x)=0.25x^2\) | \((1,0.25)\) | |
| \(p(x)=x^2\) | \((1,1)\) | |
| \(p(x)=2x^2\) | \((1,2)\) | |
| \(p(x)=4x^2\) | \((1,4)\) | |
| \(p(x)=ax^2\) | \((1,a)\) |
- ככל שהמראה הפרבולית רחבה יותר, האם המוקד יהיה קרוב יותר לקודקוד הפרבולה או רחוק יותר? נמקו תשובתכם.
- אחרי שפתרתם את השאלות בבעיית מטרה 2, המשיכו למה עוד אפשר לשאול.
- בחרו את שיעור ה- x של נקודה B:
בעזרת גרירה של B על הפרבולה, או בעזרת הזזת סרגל הגרירה \(x(B)\) - שנו את ערכי סרגל הגרירה a, ובדקו את השפעת הערך של a על מיקום המוקד (F) ועל מיקום המדריך (ישר m)
פתרון בעיית מטרה 2
פתרון בדומה לבעיית מטרה 1.
-
ביטוי אלגברי של פרבולה שיעורי נקודה \(B\) על הפרבולה שיעורי המוקד \((F)\) \(p(x)=0.25x^2\) \((1,0.25)\) \((0,1)\) \(p(x)=x^2\) \((1,1)\) \((0,1/4)\) \(p(x)=2x^2\) \((1,2)\) \((0,1/8)\) \(p(x)=4x^2\) \((1,4)\) \((0,1/16)\) \(p(x)=ax^2\) \((1,a)\) \((0,1/4a)\)
\(\space\) - ככל שהמכנה בשבר חיובי קטן יותר, ערכו של השבר גדול יותר.
לכן, אם הפרבולה רחבה יותר, אז a קטן יותר ואז 1/4a גדול יותר.
לכן, המוקד של מראה פרבולית רחבה, יהיה רחוק מקודקוד הפרבולה.
ניתן לראות זאת בתמונה הבאה:
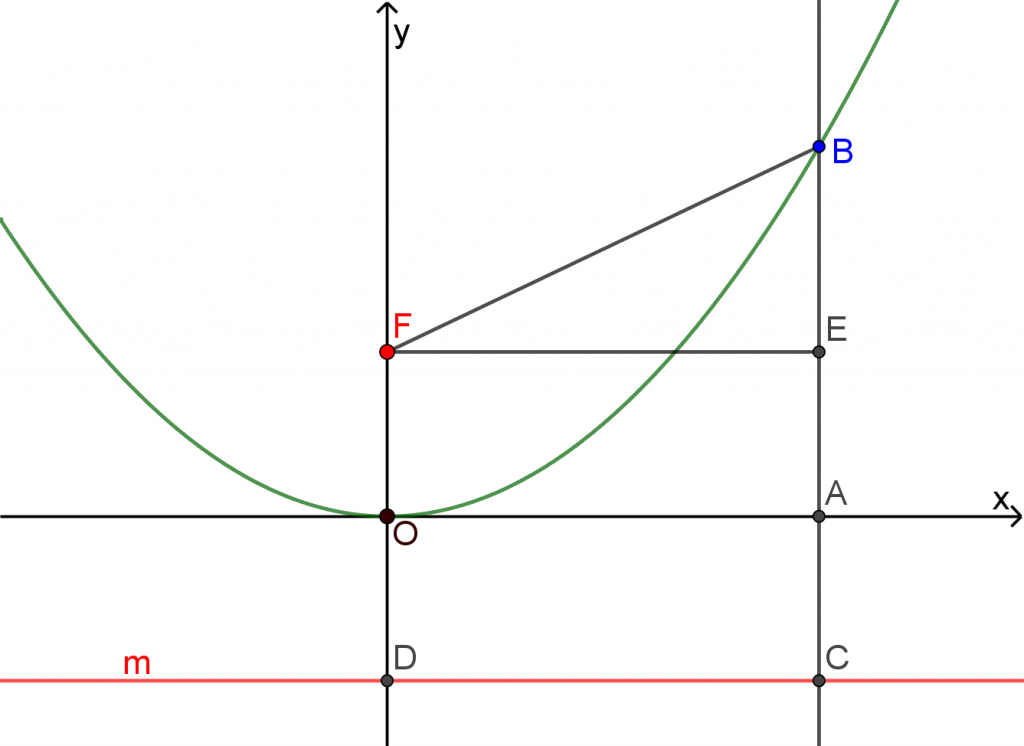
- בחרו את שיעור ה- x של נקודה B:
בעזרת גרירה של B על הפרבולה, או בעזרת הזזת סרגל הגרירה \(x(B)\) - שנו את ערכי סרגל הגרירה a, ובדקו את השפעת הערך של a על מיקום המוקד (F) ועל מיקום המדריך (ישר m)
מקורות מידע
מתוך ויקיפדיה: מראה
"מראה קעורה יכולה לשמש כקולימטור, כלומר לרכז קרני אור מקבילות לנקודה אחת, או להפך, להפוך אור המגיע מנקודה אחת לקרניים מקבילות. בפרבולה קרן אור המגיעה מנקודה מרוחקת, במקביל לציר ופוגעת בה, מוחזרת אל המוקד. גם לפרבולואיד, גוף הסיבוב של הפרבולה, יש אותה תכונה, לכן כל קרני האור המגיעות מעצם מרוחק ופוגעות במראה שצורתה פרבולואידית, מתרכזות במוקד. תכונה זו משמשת בקולט שמש ליצירת אנרגיה סולארית. בכיוון ההפוך, מקור אור, הממוקם במוקד, מפזר את אורו, דרך מראה פרבולואידית, בקווים מקבילים. לשימוש יומיומי מייצרים מראות שצורתן כיפה. אם הזווית קטנה, הכיפה מהווה קירוב לפרבולואיד, ויש לה (בקירוב) אותה תכונה של החזרת הקרניים.
מקור אור אשר יוצב בנקודת המוקד יפוזר ל"אין-סוף" על ידי המראה, עובדה בה נעשה שימוש בפנסי מכונית."