אשכול האנומליה של המים - חלק ב - צפיפות המים ופרבולה - למורה
הנחיות למורה
אשכול ב מתוך 3 אשכולות.
יחידה:
מדעים
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
מסה וצפיפות של חומרים, יחידות של מסה וצפיפות. קשר הקיים בין טמפרטורה לצפיפות. האנומליה של המים וביטוייה בתופעות שונות בטבע.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| גרפים ופונקציות | – תחום של הפונקציה – השתנות של פונקציה בקצב אחיד ובקצב לא אחיד – קנה מידה של מערכת צירים – נקודת מקסימום – תחום עליה – תחום ירידה | – הדגמה באמצעות טבלאות וגרפים כיצד פונקציה מתארת תופעה. – מהכרת הפונקציה הסקת מסקנות ותיאור של השתנות של תופעה. – קריאת גרף המדגים את תופעת האנומליה של המים. |
| פונקציה ריבועית | – קודקוד פרבולה – ציר סימטריה של פרבולה – תחום עליה – תחום ירידה | – מציאת ייצוג אלגברי לפונקציה ריבועית: ייצוג קודקודי, או ייצוג סטנדרטי. – פתרון משוואה ריבועית. |
| אומדן | – רמת דיוק של מספרים רציונליים בייצוג עשרוני | – אוריינות כמותית: חישוב, אומדן ועיגול מספרים לצורך פתרון בעיות. |
| בעיות אורייניות מתוך מציאות קרובה לתלמידים | – צפיפות, – מסה – נפח – יחידות של: מסה, נפח, צפיפות – גרף המתאר את השתנות צפיפות המים, בהתאם לטמפרטורה | – פתרון בעיות המשלבות בין הבנת טקסט מילולי והצגת נתונים הלקוחים מתוך המציאות, לביצוע החישובים המתאימים לפתרון הבעיות. – מתן הסברים לתופעות טבע. |
מטרות האשכול:
פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך. הפתרון מוביל להעמקת ההבנה כיצד להיעזר במידע המוצג בטקסט ובמידע המוצג בגרף המתאר את השפעת הטמפרטורה על השינוי בצפיפות המים ובצפיפות הקרח, כדי להכיר ולהבין את תופעת האנומליה של המים.
פתרון הבעיות באשכול מאפשר להעמיק את הידע המתמטי בנושא הפונקציה הריבועית.
מערך דידקטי מומלץ:
- בפתיחת השיעור רצוי לשאול את התלמידים שאלות לגבי צפיפות חומרים והאנומליה של המים – כתזכורת למה שלמדו באשכול "האנומליה של המים-גרף צפיפות המים-חלק א".
- ארגון הכיתה: למידה בזוגות או בקבוצות.
- ציוד נדרש: מחשבון, מחשב כדי שניתן יהיה להפעיל את היישומון (לא הכרחי).
- ניהול השיעור: המורה יאפשר לתלמידים לפתור את הבעיות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות וביישומונים. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות.
- המורה יבקש, מתלמידים שסיימו לפתור את הבעיות שבאשכול, להציע שאלה נוספת הקשורה לאשכול ולענות עליה.
- דיון בכיתה:
- התלמידים יציגו ויסבירו את תשובותיהם בדיון. רצוי לאפשר להם להציג דרכים שונות לפתרון.
- רצוי לדון בנקודות הבאות:
- כדי למצוא ביטוי אלגברי לפונקציה ריבועית – שיעורי כמה נקודות הנמצאות על הפרבולה צריכים להיות נתונים (להתייחס למקרים שונים)? זאת, לעומת קו ישר.
- אילו ייצוגים אלגבריים קיימים לפונקציה ריבועית?
- באיזה ייצוג רצוי לבחור לפתרון שאלה זו ומדוע?
- בהקשר לפתרון סעיף ג, לדון בשאלה באיזה ייצוג כדאי לנו להיעזר בפתרון המשוואה.
- יש לאפשר לתלמידים להציג את השאלות הנוספות שחשבו עליהן ולדון בפתרונות שהציעו.
- רצוי שהמורה יבחר, מבין שאלות התלמידים, את השאלות שלדעתו ראוי לדון בהן.
- אפשרות נוספת היא להציע לתלמידים להגיש את השאלות הנוספות ואת פתרונן כעבודת הגשה.
אשכול האנומליה של המים – חלק ב – צפיפות המים ופרבולה
תיאור סיטואציה
מסה – היא כמות החומר המצויה בגוף כלשהו. *
היחידה למדידת מסה היא קילוגרם (ק"ג) או גרם, מיליגרם, טון ועוד.
צפיפות החומר – היא המסה של יחידת נפח של החומר, לדוגמא המסה של סמ"ק או המסה של מ"ק .
הצפיפות נמדדת ביחידות של מסה לנפח,
כלומר, בגרם לסמ“ק (\(\large\frac{gr}{cm^3}\)) או ב- ק“ג למ"ק (\(\large\frac{kg}{m^3}\)).
* הערה: המסה של גוף אינה משתנה ממקום למקום, והיא תהיה זהה בכדור-הארץ, על פני הירח או בכל מקום אחר. לעומת זאת, משקל הגוף תלוי בכוח המשיכה הפועל עליו, ולכן יהיה משקלנו על פני הירח קטן יותר!
חומר שצפיפותו קטנה יותר, צף על גבי נוזל שצפיפותו גדולה יותר.
בתמונה משמאל משורה המכילה מספר נוזלים השונים בצפיפות שלהם. הצפוף ביותר למטה, והכי פחות צפוף למעלה.
שמן צף על מים
כאשר מחממים חומר מסתו אינה משתנה, אבל צפיפותו משתנה. כמעט בכל החומרים הצפיפות קטנה כאשר הטמפרטורה עולה.
כאשר מקררים חומר בדרך כלל צפיפותו גדלה.
למשל, כשמקפיאים שמן צפיפותו גדלה. שמן קפוא צפיפותו גדולה יותר מצפיפות שמן נוזלי. ולכן אם נכניס קוביית שמן קפוא לתוך שמן נוזלי, הקובייה תשקע.
יוצאי דופן מבחינה זו הם מים.
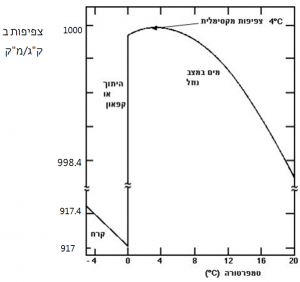
הערה: שימו לב לסימון \(\approx\) המציין "קפיצה" בערכי הצפיפות, בין 917.4 לבין 998.4, שפירושה שקנה המידה אינו אחיד.
(ניתן ללחוץ על התמונה ולהגדיל אותה)
התבוננו בגרף וענו על השאלות הבאות.
בתשובות מספריות לשאלות הבאות עליכם לתת תשובות עם דיוק של 6 ספרות אחרי הנקודה העשרונית.
צפיפות מים מתוקים ב- \(0^{\circ}C\) היא \(\large\frac{ג"ק}{ק"מ}\space\normalsize 999.87\).
פרבולה היא קירוב טוב לגרף של צפיפות המים כתלות בטמפרטורה בתחום: \(0^{\circ}C\le t \le 14^{\circ}C\).
- מצאו ביטוי אלגברי לפרבולה זו. פרטו חישוביכם. תוכלו להיעזר ביישומון המצורף.
- חשבו מהי (בקירוב) צפיפות של מים מתוקים בטמפרטורה של \(2^{\circ}C\) ובטמפרטורה של \(10^{\circ}C\)? הציגו את פתרונותיכם. תוכלו להיעזר ביישומון המצורף.
- חשבו מהי (בקירוב) הטמפרטורה של מים מתוקים שהצפיפות שלהם היא \(\large\frac{ג"ק}{ק"מ}\space\normalsize 999.48\)? הציגו את פתרונותיכם. תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- רישמו ביטוי אלגברי לפונקציה וליחצו על בדיקה.
- הפונקציה אותה רשמתם תופיע בכחול. שימו לב ליחידות המידה.
במידה וטעיתם בביטוי המבוקש, תוצג הודעה באדום. נסו שוב.
הפונקציה הנכונה תוצג בצבע ירוק.
(יש לרשום ערכים, תוך דיוק של שש ספרות אחרי הנקודה העשרונית). - ניתן להציג סרגל אנכי וסרגל אופקי, כדי לראות נקודות חיתוך על הגרף.
- במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
פתרון של בעיית מטרה 1
יש לשים לב להוראה "בתשובות מספריות לבעיות הבאות עליכם לתת תשובות עם דיוק של 6 ספרות אחרי הנקודה העשרונית". – זאת, גם כדי שניתן יהיה לבדוק את הפתרון בעזרת היישומון המצורף.
סעיף א
מציאת ביטוי אלגברי לפונקציה הריבועית \(f(t)\).
הדרך העדיפה והפשוטה ביותר היא בעזרת הייצוג הקודקודי.
דרך א
באמצעות ייצוג קודקודי:
\(f(t)=a(t-4)^2+1000\)
\(999.87=a(0-4)^2+1000\)
\(a=-0.008125\)
\(f(t)=-0.008125(t-4)^2+1000\)
ישנן דרכים נוספות למציאת ביטוי אלגברי לפונקציה הריבועית, כפי שמפורט בהמשך:
דרך ב
באמצעות ייצוג פולינומי:
\(f(t)=at^2+bt+c\)
\(c=999.87\)
\(t_{דוקדוק}=4=\large\frac{-b}{2a}\)
\(b=-8a\)
\(1000=16a-8a\cdot4+999.87\)
\(a=-0.008125\approx-0.008\)
\(b=0.065\)
\(f(t)=-0.008125t^2+0.065t+999.87\)
דרך ג
\(f(t)=at^2+bt+c\)
\(c=999.87\)
הצבת הקודקוד: \((4,1000)\) ונקודה סימטרית לנקודה \((0,999.87)\) שהיא: \((8,999.87)\)
\(1000=16a+4b+999.87\)
\(999.87=64a+8b+999.87\)
\(a=\large\frac{-b}{8}\)
\(1000=2b+999.87\)
\(b=0.065\)
\(a=-0.008125\)
\(f(t)=-0.008125t^2+0.065t+999.87\)
סעיף ב
\(f(2)=\large\frac{ג"ק}{ק"מ}\space\normalsize 999.9675\)
\(f(10)=\large\frac{ג"ק}{ק"מ}\space\normalsize 999.7075\)
סעיף ג
\(-0.008125(t-4)^2+1000=999.48\)
\((t-4)^2=\large\frac{999.48-1000}{-0.008125}\normalsize=64\)
\(t-4=8\) או \(t-4=-8\)
\(t=12\) או \(t=-4\)
\(t=-4\) אינו נמצא בתחום הנתון, ולכן אינו מתקבל
ב- \(12^{\circ}C\) צפיפות המים היא בקירוב \(\large\frac{ג"ק}{ק"מ}\space\normalsize 999.48\)
פתרון לבעיית מטרה 1
האנומליה של המים באה לידי ביטוי בתחום שבין \(0^{\circ}C\) ל- \(4^{\circ}C\). בתחום זה ככל שהטמפרטורה של המים גדלה, צפיפות המים גדלה, ואילו בחומרים אחרים ככל שהטמפרטורה של החומר גדלה, צפיפות החומר קטנה.
ב- \(0^{\circ}C\), כאשר הקרח מפשיר למים, חלה עליה ניכרת בצפיפות המים.
1.1 מדרגה 1 לבעיית מטרה 1
נתון הגרף משמאל.
בעיה 1.1.1
- מהי הצפיפות המקסימלית של המים?
- פרבולה היא קירוב טוב לגרף של צפיפות המים כפונקציה של טמפרטורה בתחום: \(0^{\circ}C\le t \le 14^{\circ}C\) (ראו גרף נתון).
ידוע כי ב- \(0^{\circ}C\) צפיפות המים היא 999.87 ק"ג/מ"ק, מהי צפיפות המים (בקירוב) ב- \(8^{\circ}C\)? נמקו.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- במידת הצורך, פתרו את השאלות במדרגה 2.
הערה: שימו לב לסימון \(\approx\) המציין "קפיצה" בערכי הצפיפות,
בין 917.4 לבין 998.4, שפירושה שקנה המידה אינו אחיד.
(ניתן ללחוץ על התמונה ולהגדיל אותה)
פתרון של מדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
- הצפיפות המקסימלית של המים היא 1000 ק"ג/מ"ק.
- כיוון שקודקוד הפרבולה הוא ב- \(t=4\), אז \(f(8)=f(0)=\large\frac{ג"ק}{ק"מ}\space\normalsize 999.87\).
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
סעיף א' של הבעיה במדרגה, ממפנה את תשומת לב התלמיד לגרף. ממנו ניתן לדעת מהי הצפיפות המקסימלית של המים.
סעיף ב' של הבעיה במדרגה, מטרתו להדגיש את הסימטריות של הפרבולה סביב הקדקוד. (כך שניתן להסיק שנתונות לנו 3 נקודות על הפרבולה: קדקוד הפרבולה, נקודת החיתוך שלה עם ציר ה- y, והנקודה ששיעור ה- x שלה הוא 8).
1.2 מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
בסרטוט שלפניכם נתונה פרבולה.
נקודה \(A(2,-4)\) היא קדקוד הפרבולה,
נקודה \(B(0,12)\) היא נקודת החיתוך של הפרבולה עם ציר ה- y.
אילו ביטויים אלגבריים מבין הביטויים הבאים מתאימים לפרבולה הנתונה בסרטוט. נמקו תשובתכם:
- \(y=(x-1)(x-3)\)
\(\space\) - \(y=4(x+2)^2-4\)
\(\space\) - \(y=4x^2-16x+12\)
\(\space\) - \(y=2(x-1)(x-6)\)
\(\space\) - \(y=4(x-2)^2-4\)
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
פתרון למדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
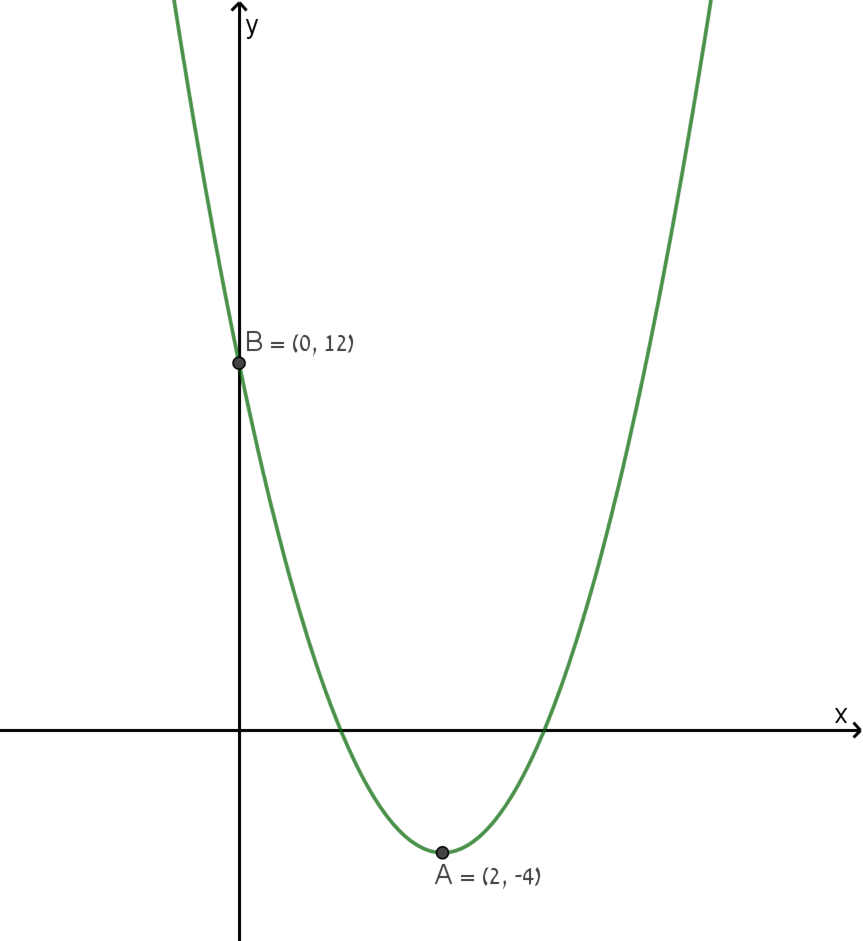
הביטויים המתאימים הם ג' ו- ה':
\(y=4x^2-16x+12\)
\(y=4(x-2)^2-4\)
רצוי לבקש מהתלמיד להסביר לגבי כל אחד מהביטויים האחרים – מה מתאים לפרבולה הנתונה ומה לא מתאים.
לדוגמה בביטוי \((x-1)(x-3)\), שיעור ה- x של הקדקוד הוא 2, כמו בפרבולה הנתונה, אך שיעור y של הקדקוד לא מתאים וכן נקודת החיתוך עם ציר ה- y אינה מתאימה.
הביטוי \(4(x-1)(x-3)\) מתאים לפרבולה הנתונה.
מטרת מדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
מטרת מדרגה זו להזכיר לתלמיד מהם שלושת הייצוגים האלגבריים האפשריים לפרבולה, כדי שיבחר בייצוג המתאים ביותר כדי לחשב את הביטוי האלגברי של הפרבולה בבעיית מטרה 1.
- סדרת התמונות הבאות מסבירה מדוע דגים יכולים להתקיים באגמים עמוקים הקופאים בחורף.
הסבירו את התופעות המתוארות בתמונות.
הערה: שימו לב לסימון \(\approx\) המציין "קפיצה" בערכי הצפיפות, בין 917.4 לבין 998.4, שפירושה שקנה המידה אינו אחיד.
(ניתן ללחוץ על תמונת הגרף ולהגדיל אותה)
- אילו תופעות נוספות אתם מכירים, הקשורות לאנומליה של המים?
- אחרי שפתרתם את בעיית מטרה 2, המשיכו למה עוד אפשר לשאול.
פתרון של בעיית מטרה 2 (סיכום)
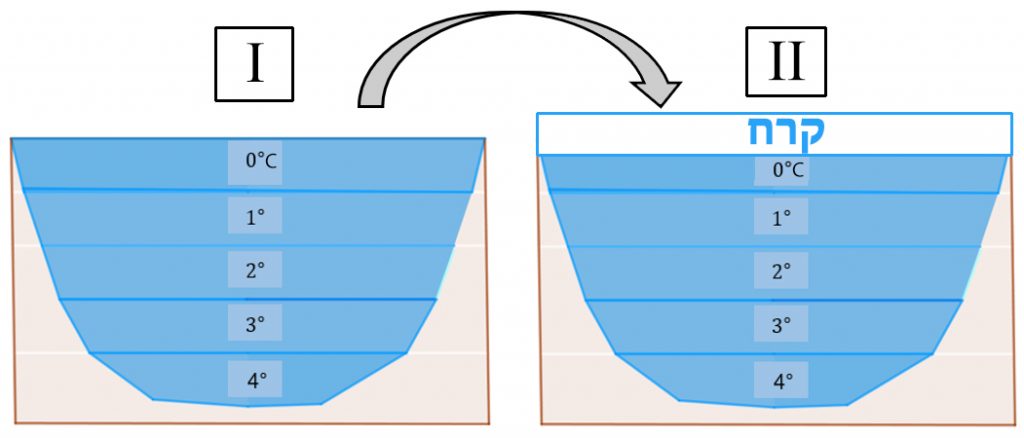
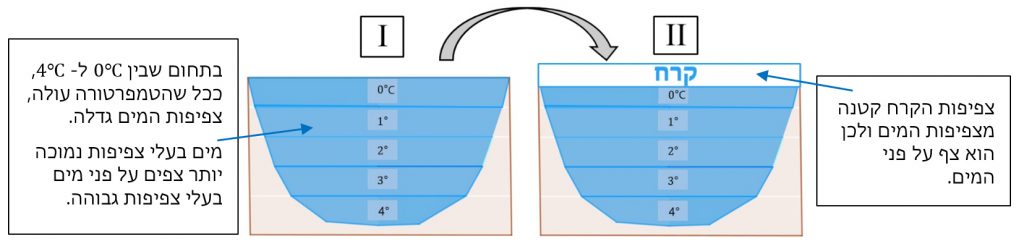
- עקב האנומליה של המים בטמפרטורות שבין \(0^{\circ}C\) ל- \(4^{\circ}C\) ככל שהטמפרטורה גבוהה יותר צפיפות המים גדולה יותר. בתמונה \(I\) רואים ששכבת המים בטמפרטורה של \(4^{\circ}C\) היא בתחתית האגם כיוון שצפיפות המים בשכבה זו היא הגבוהה ביותר, שכבת המים בטמפרטורה של \(3^{\circ}C\) היא מעליה כיוון שצפיפות המים בטמפרטורה של \(3^{\circ}C\) קטנה מצפיפות המים בטמפרטורה של \(4^{\circ}C\) וכך הלאה. צפיפות המים בטמפרטורה של \(0^{\circ}C\) היא הקטנה ביותר ולכן הם מהווים את השכבה העליונה במימי האגם.
\(\space\)
בתמונה \(II\) שכבת המים העליונה באגם קפאה והפכה לקרח. עקב האנומליה של המים צפיפות הקרח קטנה ביותר מ-8% מצפיפות המים ב- \(0^{\circ}C\) ולכן שכבת הקרח היא עליונה ומכסה את האגם.
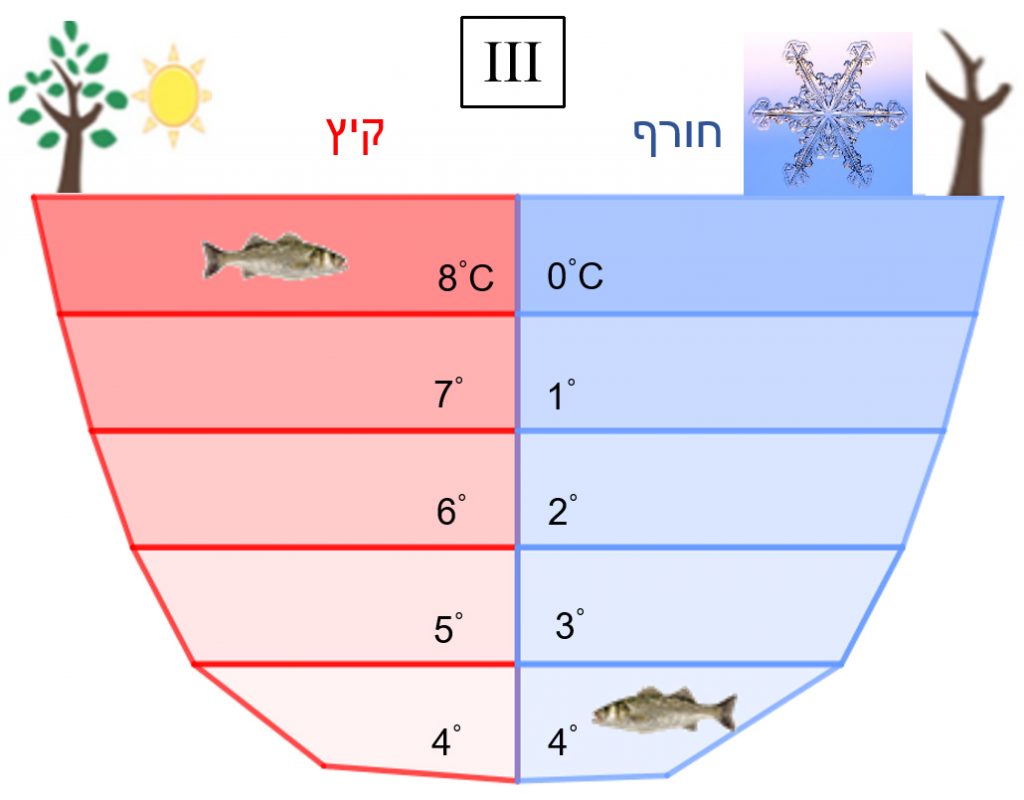
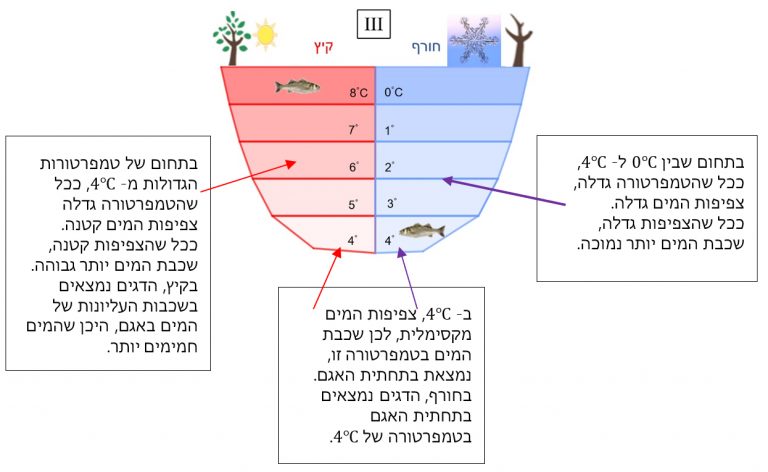
הדגים בחורף יכולים לחיות בתחתית האגם היכן שהטמפרטורה של המים היא \(4^{\circ}C\) (תמונה \(III\))
בקיץ המים מתחממים מעבר ל- \(4^{\circ}C\). בטמפרטורות אלה ככל שהטמפרטורה גבוהה יותר צפיפות המים קטנה. השכבה העליונה באגם היא בטמפרטורה הגבוהה ביותר- כיוון שצפיפות המים בשכבה זו היא הקטנה ביותר. ובתחתית האגם שכבת המים בטמפרטורה של \(4^{\circ}C\) שצפיפות המים בה היא מקסימלית.
הצעה לשאלה נוספת
מהי צפיפות הקרח (בקירוב) ב- \(-3^{\circ}C\)? (כחזרה וביסוס הידע על קו ישר).
מידע נוסף:
כאשר הקרחון צף מעל פני המים, הוא משמש כמבודד בין הסביבה החיצונית לסביבה המימית ומונע שינויים דרסטיים בטמפרטורה כגון התחממות יתר או קפיאה. בקוטבי כדור הארץ ניתן לראות זאת באופן משכנע – לולא היו הקרחונים צפים מעל פני המים ומהווים שכבה מבודדת, היו כל המים קופאים כאשר מחוץ להם הייתה ירידה דרסטית בטמפרטורה, ובעלי חיים לא היו יכולים להתקיים בתוך המים.
צפיפות המים
צפיפות המים מוגדרת כמשקל של יחידת-נפח של מים.
כידוע, עולה צפיפותם של נוזלים עם ירידת הטמפרטורה עד נקודת הקיפאון. למים אנומאליה במקרה זה: צפיפות המים המקסימאלית היא ב- 4°C וערכה אז הוא 1g לסמ"ק מים, ובטמפרטורות נמוכות יותר הצפיפות יורדת עוד.
לשון אחרת – כאשר הטמפרטורה יורדת מתחת ל- 4°C נפח המים עולה עד אשר ב- 0° הם קופאים לקרח – שצפיפותו קטנה ב- 10% בקירוב מצפיפות המים. חשיבותה של עובדה זו היא עצומה אם נזכור שבגלל זה יצוף הקרח, הקל יותר, על פני המים. הדבר מאפשר המשך קיום החיים במים מתחת לפני הקרח.
מקור: צפיפות המים
מקורות:
גרף – מאפיינים פיזיקליים של המים