אשכול האנומליה של המים - חלק ג - נפח המים - למורה
יישומונים
- – – – – –
- – – – – –
- יישומון למדרגה 2
- – – – – –
- – – – – –
- – – – – –
הנחיות למורה
אשכול ג מתוך 3 אשכולות.
יחידה:
מדעים
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
קשר בין צפיפות חומר לנפחו, השפעת טמפרטורה על נפח של חומר, האנומליה של המים בהקשר לנפח המים ונפח הקרח, תופעות טבע הקשורות לאנומליה של המים.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| גרפים ופונקציות | – תחום של הפונקציה – השתנות של פונקציה בקצב אחיד ובקצב לא אחיד – קנה מידה של מערכת צירים – נקודת מקסימום – נקודת מינימום – תחום עליה – תחום ירידה | – הדגמה באמצעות טבלאות וגרפים כיצד פונקציה מתארת תופעה. הסקת מסקנות ותיאור של השתנות של תופעה. – קריאת גרף המדגים את השתנות צפיפות המים והקרח בהתאם להשתנות הטמפרטורה. – בניית טבלת ערכים המדגימה את השתנות נפח המים והקרח בהתאם להשתנות הטמפרטורה |
| ארגון נתונים בדרכים שונות | – גרף של נקודות במערכת צירים – טבלת ערכים | – סימון נקודות במערכת צירים (המתארות את השתנות נפח של חומר בהתאם לטמפרטורה) – הבנה של מגמת שינוי של נתונים. |
| יחס | – יחס בין גדלים שאינם מאותו סוג: – נוסחת צפיפות (יחס בין מסה לנפח) | – הבנה כי: כאשר היחס הוא בין גדלים מסוגים שונים, אז ליחס יש יחידות מידה. (יחס בין מסה לנפח) |
| יחס הפוך | – יחס הפוך (הקשר בין צפיפות חומר לנפח החומר כאשר המסה קבועה) | – הבנה כי: שני גדלים חיוביים (צפיפות ונפח) משתנים, כאשר המכפלה שלהם קבועה (מסה), מקיימים יחס הפוך. כלומר: כאשר נתונים שני גדלים חיוביים, (צפיפות חומר ונפח חומר), כך שכשגודל אחד (צפיפות) קטן (או גדל) פי מספר מסוים – הגודל השני (נפח) גדל (או קטן) פי אותו המספר, אז בין שני הגדלים יש יחס הפוך. – חישוב המתבסס על היחס ההפוך בין צפיפות לנפח. |
| יחידות מידה | – יחידות מידה של נפח – מ"ק, סמ"ק | – מעבר בין יחידות מידה של נפח |
| אומדן | – רמת דיוק של מספרים רציונליים בייצוג עשרוני | – אוריינות כמותית: חישוב, אומדן ועיגול מספרים לצורך פתרון בעיות |
| בעיות אורייניות מתוך מציאות קרובה לתלמידים | – צפיפות, – מסה – נפח – יחידות של: מסה, נפח, צפיפות – גרף המתאר את השתנות צפיפות המים בהתאם לטמפרטורה | – פתרון בעיות המשלבות בין הבנת טקסט מילולי והצגת נתונים הלקוחים מתוך המציאות לביצוע החישובים המתאימים לפתרון הבעיות – מתן הסברים לתופעות טבע |
מטרות האשכול:
פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות במתמטיקה בהתאם לתוכנית הלימודים של משרד החינוך. הפתרון מוביל להעמקת ההבנה כיצד להיעזר בקריאה ובהבנת גרף מפוצל המתאר את השפעת הטמפרטורה על צפיפות המים וצפיפות הקרח, בשילוב ההבנה של משמעות הנוסחה המקשרת בין צפיפות חומר לנפחו, זאת כדי לתאר את תופעת האנומליה של המים מבחינת השפעת השתנות הטמפרטורה על השתנות נפח המים ונפח הקרח.
פתרון הבעיות שבאשכול דורש יישום ידע ומיומנויות מתמטיים בהתאם לתוכנית הלימודים של משרד החינוך ומוביל להעמקת ההבנה של: קריאה והבנת משמעותו של גרף מפוצל, שימוש בנוסחה לביצוע חישובים, יחס הפוך וייצוגו הגרפי, מעבר בין יחידות של נפח, עיגול מספרים עשרוניים.
ידע מתמטי ומיומנויות מתמטיים נלמדים (חדשים):
- קריאה והבנה של גרף מפוצל.
- הבנת משמעות קנה מידה בגרף.
- הצבה בנוסחה וביצוע חישובים בעזרת הנוסחה.
- יחס הפוך, והבנת השפעת המכנה על גודל השבר.
- הקשרים הקיימים בין מאפיינים של גרף נתון של פונקציה לבין מאפיינים של הפונקציה ההופכית לה.
- מעבר בין יחידות של נפח.
- הבנה לעומק של טקסט מילולי.
מערך דידקטי מומלץ:
- רצוי להקדים ולשאול את התלמידים שאלות הקשורות למה שלמדו על האנומליה של המים באשכולות הקודמים: האנומליה של המים – גרף צפיפות המים – חלק א והאנומליה של המים – צפיפות המים ופרבולה – חלק ב.
- את הפתיח, הסבר לגבי נפח של חומרים ותלותו בטמפרטורה, ניתן לקרוא ביחד בכיתה.
- רצוי להציג בפני כל הכיתה את קטע הווידאו המוצג בפתיח, הממחיש את השפעת הטמפרטורה על הנפח של כדור מתכת.
- ארגון הכיתה: למידה בזוגות או בקבוצות.
- ציוד נדרש: מחשבון, מחשב.
- ניהול השיעור: המורה יאפשר לתלמידים לפתור את הבעיות שבאשכול באופן עצמאי, כשבאפשרותם להיעזר במדרגות וביישומונים. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות.
- המורה יבקש, מתלמידים שסיימו לפתור את הבעיות שבאשכול, להציע שאלה נוספת הקשורה לאשכול ולענות עליה.
- דיון בכיתה:
התלמידים יציגו ויסבירו את תשובותיהם בדיון. רצוי לאפשר להם להציג דרכים שונות לפתרון.
יש להדגיש בדיון שהגרף של השתנות נפח המים כתלות הטמפרטורה אמנם "דומה" לפרבולה, אך אינו פרבולה.
והגרף של השתנות נפח הקרח כתלות בטמפרטורה, אינו קו ישר. - יש לאפשר לתלמידים להציג את השאלות הנוספות שחשבו עליהן ולדון בפתרונות שהציעו.
רצוי שהמורה יבחר, מבין שאלות התלמידים, את השאלות שלדעתו ראוי לדון בהן.
אפשרות נוספת היא להציע לתלמידים להגיש את השאלות הנוספות ואת פתרונן כעבודת הגשה.
אשכול האנומליה של המים – חלק ג – נפח המים
תזכורת
באשכולות הקודמים, האנומליה של המים – גרף צפיפות המים – חלק א והאנומליה של המים – צפיפות המים ופרבולה – חלק ב, למדנו כי:
מסה – היא כמות החומר המצויה בגוף כלשהו.
היחידה למדידת מסה היא קילוגרם (ק"ג) או גרם, מיליגרם, טון ועוד.
צפיפות החומר – היא המסה של יחידת נפח של החומר, לדוגמא המסה של סמ"ק או המסה של מ"ק .
הצפיפות נמדדת ביחידות של מסה לנפח,
כלומר, בגרם לסמ“ק (grcm3grcm3) או ב- ק“ג למ"ק (kgm3).
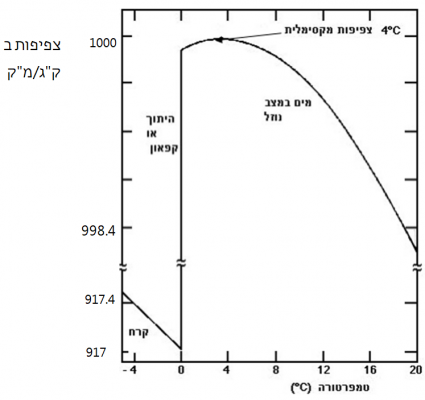
בדקנו כיצד משתנה צפיפות המים והקרח (מים במצב מוצק) בהתאם לשינוי בטמפרטורה שלהם.
ראינו שבעוד שבדרך כלל, כאשר מחממים חומר צפיפותו יורדת ולכן גם צפיפותו של מוצק גדולה מצפיפותו של נוזל של אותו חומר, במים קיימת אנומליה:
צפיפות הקרח ב- 0∘C קטנה מצפיפות המים ב- 0∘C.
כאשר מחממים את המים מ- 0∘C עד 4∘C צפיפותם תעלה.
כאשר נמשיך לחמם אותם מעבר לטמפרטורה של 4∘C צפיפותם תרד.
תיאור סיטואציה
באשכול זה נעסוק בקשר בין צפיפות החומר לנפחו ונתמקד בהשתנות נפח חומר כתלות בטמפרטורה.
כאשר מחממים חומר מסתו אינה משתנה, אבל נפחו משתנה. כמעט בכל החומרים הנפח גדל, וכאשר מקררים חומר בדר"כ ניפחו קטן.
לדוגמה:
כדור מתכת עובר בתחילה בקלות דרך דסקית. חימום כדור המתכת יגרום לכך שהוא לא יעבור דרך הדסקית, כיוון שנפח כדור המתכת גדל.
צפו בסרטון הווידאו: https://www.youtube.com/watch?v=QNoE5IoRheQ
לפני חימום של הכדור, הוא עובר בקלות דרך הדסקית

אחרי חימום הכדור, הוא אינו עובר דרך הדסקית

התמונות נלקחו מסרטון הווידאו: https://www.youtube.com/watch?v=QNoE5IoRheQ
כאשר נחמם אוויר בתוך כדור פורח, נפח האוויר גדל ומנפח את הכדור.
חימום האוויר בתוך הבלון


במדחום כספית, נפח הכספית יגדל כאשר החום יעלה, ולכן גובה הכספית יעלה, ככל שהחום יהיה גבוה יותר.
יוצאי דופן מבחינה זו הם המים.
במשימה הנוכחית, נרצה לבחון את הקשר בין נפח המים והטמפרטורה שלהם.
תופיפצ=הסמחפנ
בתשובות מספריות לבעיות הבאות עליכם לתת תשובות סופיות בדיוק של 3 ספרות אחרי הנקודה העשרונית.
- צפיפות 1 ק"ג מים מתוקים ב- 0∘C היא 999.87 ק"ג/מ"ק. ב- 0∘C המים קופאים והופכים לקרח.
א1. מי גדול יותר: נפח המים ב- 0∘C, או נפח הקרח ב- 0∘C? נמקו.
א2. כאשר המים קופאים, בכמה סמ"ק משתנה הנפח של 1 ק"ג מים? - היעזרו בגרף הנתון ובנוסחת הצפיפות,
ב1. תארו במילים את השתנות הנפח של 1 ק"ג מים מתוקים כאשר מחממים אותם מ- 0∘C עד ל- 14∘C.
ב2. הסבירו מדוע המים יוצאי דופן מבחינת השתנות נפח המים, כתלות בטמפרטורה. פרטו ונמקו תשובתכם. - תארו במילים את השתנות הנפח של 1 ק"ג קרח, כאשר מחממים אותו מ- −4∘C עד ל- 0∘C.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון לבעיית מטרה 1
א1. נפח של 1 ק"ג מים מתוקים ב- 0∘C הוא 1999.87⋅106=ק"מס 1000.13.
א2. 1000.13−106917=ק"מס (−90.383)
כאשר 1 ק"ג מים קופאים נפחם קטן ב- 90.383 סמ"ק.
ב1. חפנ=הסמתופיפצ
- מסה של חומר אינה משתנה. מהנוסחה ניתן להבין שנפח של חומר נמצא ביחס הפוך לצפיפותו. כלומר, ככל שהצפיפות גדלה הנפח קטן, וככל שהצפיפות קטנה הנפח גדל.
- בתחום 4∘C<t≤14∘C, הגרף מראה שצפיפות המים קטנה ככל שהטמפרטורה גדלה. כלומר, בתחום זה, ככל שהטמפרטורה גדלה, נפח המים גדל.
 בתחום 0∘C<t<4∘C, הגרף מראה שצפיפות המים גדלה ככל שהטמפרטורה גדלה. כלומר, בתחום זה, ככל שהטמפרטורה גדלה, נפח המים קטן.
בתחום 0∘C<t<4∘C, הגרף מראה שצפיפות המים גדלה ככל שהטמפרטורה גדלה. כלומר, בתחום זה, ככל שהטמפרטורה גדלה, נפח המים קטן.- מסקנה: ב- 4∘C נפח המים הוא מינימלי.
ב2. האנומליה של המים מבחינת נפחם באה לידי ביטוי בתחום הטמפרטורות 0∘C<t≤4∘C. בתחום זה, ככל שהטמפרטורה גדלה, נפח המים קטן, ואילו כמעט בכל החומרים האחרים, ככל שהטמפרטורה גדלה, נפח החומר גדל.
נוסף לכך ב- 0∘C כאשר הקרח מפשיר והופך למים, בטמפרטורה של 0∘C, נפח המים קטן במידה ניכרת מנפח הקרח, בעוד שבחומרים אחרים, כאשר הם עוברים ממוצק לנוזל, נפחם גדל.
ג. בתחום −4∘C<t≤0∘C, ככל שהטמפרטורה גדלה, צפיפות הקרח קטנה. לכן, בתחום זה, ככל שהטמפרטורה גדלה, נפח הקרח גדל.
תופיפצ=הסמחפנ
- מי גדול יותר: הנפח של 1 ק"ג מים בטמפרטורה של 2∘C, או הנפח של 1 ק"ג מים בטמפרטורה של 0∘C?
- מי גדול יותר: הנפח של 1 ק"ג מים בטמפרטורה של 10∘C, או הנפח של 1 ק"ג מים בטמפרטורה של 4∘C?
נמקו תשובותיכם.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
פתרון למדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
- נפח של 1 ק"ג מים בטמפרטורה של 0∘C, גדול מנפח של 1 ק"ג מים בטמפרטורה של 2∘C.
- נפח של 1 ק"ג מים בטמפרטורה של 10∘C, גדול מנפח של 1 ק"ג מים בטמפרטורה של 4∘C.
מטרת מדרגה 1 של בעיית מטרה 1
בעיה 1.1.1
- הפניית תשומת לב התלמיד לכך שניתן להסיק מסקנות לגבי סדר הגודל של נפח המים בטמפרטורות שונות (באיזו טמפרטורה הנפח גדול יותר), מתוך גרף צפיפות המים, ללא צורך בחישובים מדויקים.
- הפניית תשומת לב התלמיד לכך שיש להתייחס לתחומי טמפרטורה שונים, כשמתארים את השתנות נפח המים, כתלות בטמפרטורה.
השלימו את הטבלה הבאה:
(בתשובה הסופית דייקו דיוק של שלוש ספרות אחרי הנקודה העשרונית ופרטו חישוביכם).
תזכורת: 106=1,000,000
| נקודה | טמפרטורה | צפיפות של ק"ג מים מתוקים ב- ג"קק"מ (בקירוב) | נפח של ק"ג מים מתוקים בסמ"ק (בקירוב) |
|---|---|---|---|
| A | 0∘C | 999.87 | |
| B | 2∘C | 999.9675 | |
| C | 4∘C | 1000 | 11000⋅106= =ק"מס 1000 |
| D | 6∘C | 999.9675 | |
| E | 8∘C | 999.87 | |
| F | 10∘C | 999.7075 | 106999.7075= =1000.292586≈ ≈ק"מס 1000.293 |
| G | 12∘C | 999.48 |
הערה: הנתונים של צפיפות המים שמופיעים בטבלה חושבו בקירוב, על פי הביטוי האלגברי לפונקציה הריבועית, שהיא פונקציית הקירוב לצפיפות המים, כפי שחושבה באשכול "האנומליה של המים – צפיפות המים ופרבולה – חלק ב".
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 3.
- שנו את הערכים בסרגל הגרירה שבחלק העליון, כדי לקבוע שיעורי x של נקודות.
- צפו בשיעורי ה-y המתאימים, והשלימו את הנקודות בחלק התחתון, ואת הערכים החסרים בטבלה.
- אם הנקודה נכונה צבעה כחול, אם אינה נכונה צבעה אדום.
(יש לעגל את הערכים, תוך דיוק של שלוש ספרות אחרי הנקודה העשרונית). - להגדלה/להקטנה של הגרף, יש ללחוץ בעכבר על כל אחד מ-2 החלקים שביישומון, ואז לגלגל את גלגלת העכבר.
- לאיתחול מחדש של היישומון, יש ללחוץ על חיצי האתחול
 שבפינה הימנית העליונה.
שבפינה הימנית העליונה.
פתרון למדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
| נקודה | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| טמפרטורה | 0∘C | 2∘C | 4∘C | 6∘C | 8∘C | 10∘C | 12∘C |
| צפיפות של ק"ג מים מתוקים ב- ג"קק"מ (בקירוב) | 999.87 | 999.9675 | 1000 | 999.9675 | 999.87 | 999.7075 | 999.48 |
| נפח של ק"ג מים מתוקים בסמ"ק (בקירוב) | 1000.13 | 1000.033 | 11000⋅106= =ק"מס 1000 | 1000.033 | 1000.13 | 106999.7075= =1000.292586≈ ≈ק"מס 1000.293 | 1000.52 |
הערה: הנתונים של צפיפות המים שמופיעים בטבלה, חושבו בקירוב על פי הביטוי האלגברי לפונקציה הריבועית, שהיא פונקציית הקירוב לצפיפות המים, כפי שחושבה באשכול "האנומליה של המים – צפיפות המים ופרבולה – חלק ב".
מטרת מדרגה 2 של בעיית מטרה 1
בעיה 1.2.1
בבעיה שבמדרגה, מוצגת שוב הנוסחה המקשרת בין צפיפות חומר לנפחו, ומוצגת טבלה המקשרת בין טמפרטורה לצפיפות המים ונפח המים. חלק מהחישובים מוצגים. בכך המדרגה עוזרת לתלמיד בכמה היבטים:
- להבין כיצר להיעזר בנוסחה כדי לחשב נפח כאשר הצפיפות נתונה.
- להבין כיצד לחשב את הנפח ביחידות של סמ"ק.
- להבין את ההוראה: בתשובה הסופית דייקו דיוק של שלוש ספרות אחרי הנקודה העשרונית.
- לעקוב אחר השתנות הנפח של מים, בהתאם לטמפרטורה.
- להבין שבין נפח לצפיפות קיים יחס הפוך, כאשר המסה היא קבועה.
למדרגה זו מצורף יישומון העוזר לתלמיד לבדוק את תשובותיו. כמו כן היישומון מאפשר להציג בצורה חזותית את השתנות נפח המים בהתאם לטמפרטורה בתחום הנתון.
הערה: פונקציית הנפח בהתאם לטמפרטורה היא פונקציה הופכית לפונקציית הצפיפות בהתאם לטמפרטורה.
תלמיד לא מתבקש לשרטט את גרף הנפח של המים בהתאם לטמפרטורה, ולמצוא לו ביטוי אלגברי, אלא רק לחשב (ולסמן ביישומון) נקודות בודדות. זאת כדי למנוע היווצרות אפשרית של תפיסה מוטעית שגרף של הפונקציה ההופכית לפרבולה הוא גם פרבולה, גם אם במקרים מסוימים ובתחום מסוים גרף הפונקציה ההופכית של פונקציה ריבועית יכול להיות "דומה" לפרבולה.
כמו כן, פונקציה הופכית לקו ישר (נפח הקרח), אינה קו ישר.
תופיפצ=הסמחפנ
בחרו את התשובות הנכונות (יש יותר מתשובה אחת נכונה) ונמקו:
נפח 1 ק"ג קרח ב- −4∘C הוא:
- 1.09004 סמ"ק
- 1090.037 סמ"ק
- 1090.5 סמ"ק
- 1,000,000917.4 סמ"ק
- אחרי שפתרתם את השאלות במדרגה 3, חזרו לבעיית מטרה 1.
פתרון למדרגה 3 של בעיית מטרה 1
בעיה 1.3.1
נפח 1 ק"ג קרח ב- −4∘C הוא:
ב. 1090.037 סמ"ק
ד. 1,000,000917.4 סמ"ק
מטרת מדרגה 3 של בעיית מטרה 1
בעיה 1.3.1
הבעיה במדרגה מתמקדת בנפח הקרח ב- −4∘C, ומציגה כמה תשובות אפשריות ביחידות של סמ"ק, כולל תשובה המציגה את דרך החישוב.
בכך מאפשרת המדרגה לתלמיד לשים לב לתחום בגרף המתייחס לקרח, להבין כיצד להיעזר בגרף ובנוסחה לחישוב נפח, ולהבין כיצד לחשב את הנפח ביחידות של סמ"ק.
תצורות סלע מדהימות נוצרות לאורך אלפי שנים והופכות מדבריות לבעלי נוף חייזרי קסום: תצורות סלע הנקראות לרוב, הוּדוּס (Hoodoos), שגובהן מ-1.5 מטרים ועד לגובה של בניין בן 10 קומות, ולרוב נוצרות בעקבות שני תהליכים הקשורים למזג האוויר: קיפאון וגשם, שעובדים ביחד וגורמים לשחיקת צורת הסלעים.

הפארק הלאומי ברייס קניון, יוטה: בארה"ב ההודוס נמצאים בשפע באזור הצפוני של הפארק הלאומי ברייס קניון, זאת הודות למעל 200 מחזורים של קיפאון והפשרה בשנה וממטרים קצרים אך רבים. בפארק ניתן למצוא את הכמות הגדולה ביותר של הודוס בעולם.
- האנומליה של המים תורמת להתפוררות של סלעים ולתופעת ההודוס. כיצד?
- בתמונה משמאלכם, רואים מים שקפאו בתוך מזרק שהיה מלא עד קצהו במים.
ניתן להבחין בתמונה בטיפת קרח שגלשה מהמזרק. הסבירו תופעה זו.
- אילו תופעות נוספות אתם מכירים, הקשורות לאנומליה של המים ולנִפְחָם?
- אחרי שפתרתם את בעיית מטרה 2, המשיכו למה עוד אפשר לשאול.
פתרון של בעיית מטרה 2 (סיכום)
- התפוררות סלעים ותופעת ההודוס הם תוצאה מתהליך קפיאה-הפשרה. תהליך זה מתרחש כאשר מים שמחלחלים לחריצים בסלע קופאים ומתרחבים בשל האנומליה של המים. בתהליך ההתרחבות, הקרח יכול להפעיל לחץ רב על הסלעים. לחץ זה בדרך כלל חזק יותר מכוח העמידה של הסלע, והלה נשבר ומתפרק.
- המזרק היה מלא במים, בשל האנומליה של המים, כאשר המים קפאו נפחם גדל ולכן הקרח פרץ דרך הפתח של המזרק ונוצרה טיפת הקרח.
- תופעות נוספות:
- ידוע כי אין להכניס למקפיא בקבוק זכוכית מלא במים. זאת בשל האנומליה של המים. כאשר המים בבקבוק קופאים נפחם גדל, נוצר לחץ על בקבוק הזכוכית והוא עלול להתפוצץ.
- בארצות בהן הטמפרטורות יורדות מתחת ל- 0∘C, המים בצינורות המים לבתים עלולים לקפוא, נפח הקרח גדל והצינורות עלולים להתפוצץ. כדי למנוע זאת ממליצים להשאיר בברזים זרם דק של מים וכך המים בצינורות לא קופאים.