אשכול כדורסל ג - פרבולה בשירות הכדורסלנים - למורה
יישומונים
- – – – – –
- – – – – –
مبنى العنقود
הנחיות למורה
אשכול ג מתוך 3 אשכולות. ניתן לפתור כל אשכול בנפרד.
אשכול זה עוסק במתמטיקה שימושית. באשכול מודגמות סיטואציות מעולם הכדורסל ומועלות שאלות אודות הכניסה של הכדור לסל, הגובה המקסימלי אליו יכול הכדור להגיע ומצבים שונים של מסלול הכדור בדרכו אל הסל.
יחידה:
ספורט
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
ספורט וחברה.
היכרות עם ייצוגים שונים של פונקציה ריבועית ומעבר ביניהם (אלגברי, גרפי).
היכרות עם ייצוגים אלגבריים שונים של פונקציה ריבועית (סטנדרטי, קודקודי, כמכפלה).
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| הפונקציה הריבועית וייצוגיה האלגבריים השונים (ייצוג סטנדרטי וייצוג קודקודי) | – פונקציה ריבועית – נקודת מקסימום – ציר סימטריה | – מציאת היתרונות של כל אחד מהייצוגים – מעבר בין הייצוגים |
| פתרון משוואה ריבועית ופתרון שאלות מילוליות | – נעלם – משוואה – פתרון של משוואה – שקילות של משוואות | יצירת משוואות שקולות |
| משמעות אלגברית ומשמעות גרפית של נקודה הנמצאת על הגרף | – שיעורי נקודה – נקודה שנמצאת על גרף הפונקציה – נקודה שמקיימת את משוואת הפונקציה | זיהוי נקודות שנמצאות על גרף הפונקציה הריבועית |
| משפחות של פונקציות ריבועיות (מתיחה, כיווץ, שיקוף) | – מתיחה – כיווץ – שיקוף | מציאת תכונות משותפות למשפחות של פונקציות ריבועיות |
מטרות האשכול
- להראות שימושיות המתמטיקה במצבים מעולם הכדורסל.
- להיעזר בייצוגים שונים של הפונקציה הריבועית כדי לתאר מסלול של כדורסל.
- למצוא פרבולות ומשוואות שלהן שמתארות מקרים בהם הכדור ייכנס/ לא ייכנס לסל.
- למצוא גובה מקסימלי אליו יכול הכדור להגיע (נקודת המקסימום של הפונקציה).
ארגון כיתה מומלץ
פתרון בעיות המטרה יתבצע בקבוצות. אחרי העבודה בקבוצות ייערך דיון במליאה.
ניהול השיעור: המורה יאפשר לתלמידים לקרוא ולהבין את המידע הנתון, להתמודד עם בעיות המטרה בקבוצות, כשבאפשרותם להיעזר במדרגות.
המדרגות מיועדות לשני הסעיפים של בעיית המטרה. המורה יעודד תלמידים שמתקשים להיעזר במדרגות, וידריך את התלמידים במקרה שישנן אי הבנות.
יש לאפשר שימוש במחשבון.
שאלות מומלצות לדיון כיתתי
- מה הקשר בין כדורסל לבין פונקציה ריבועית?
- תנו דוגמאות נוספות מחיי היום-יום למצבים בהם יש שימוש לפרבולה, למשל: גופים שנעים במסלול פרבולי.
- כמה פונקציות ריבועיות שונות עוברות דרך שתי נקודות נתונות (שאינן על ישר אחד)?
- כיצד משפיע סימנו של a (המקדם של x2x2) על צורת הפרבולה?
- כיצד משפיע b (המקדם של xx) על צורת הפרבולה?
- כיצד משפיע c (האיבר החופשי) על צורת הפרבולה?
סרטונים ופעילויות לשילוב בפתיחה או בהמשך
אשכול כדורסל ג – פרבולה בשירות הכדורסלנים
תיאור סיטואציה
במשחק כדורסל שחקן זורק כדור במטרה לקלוע לסל.
האיורים מתארים את מסלול הכדור בדרכו אל הסל (או מחוץ לסל), את מיקומו של השחקן ואת מיקומו של הסל.
המסלול שעובר הכדור הוא גרף של פרבולה.
באשכול זה ניעזר בייצוגים האלגבריים השונים של הפונקציה הריבועית כדי לתאר את המסלול של הכדור וכך נוכל לגלות באילו מקרים הכדור יכנס לסל ובאילו לא.
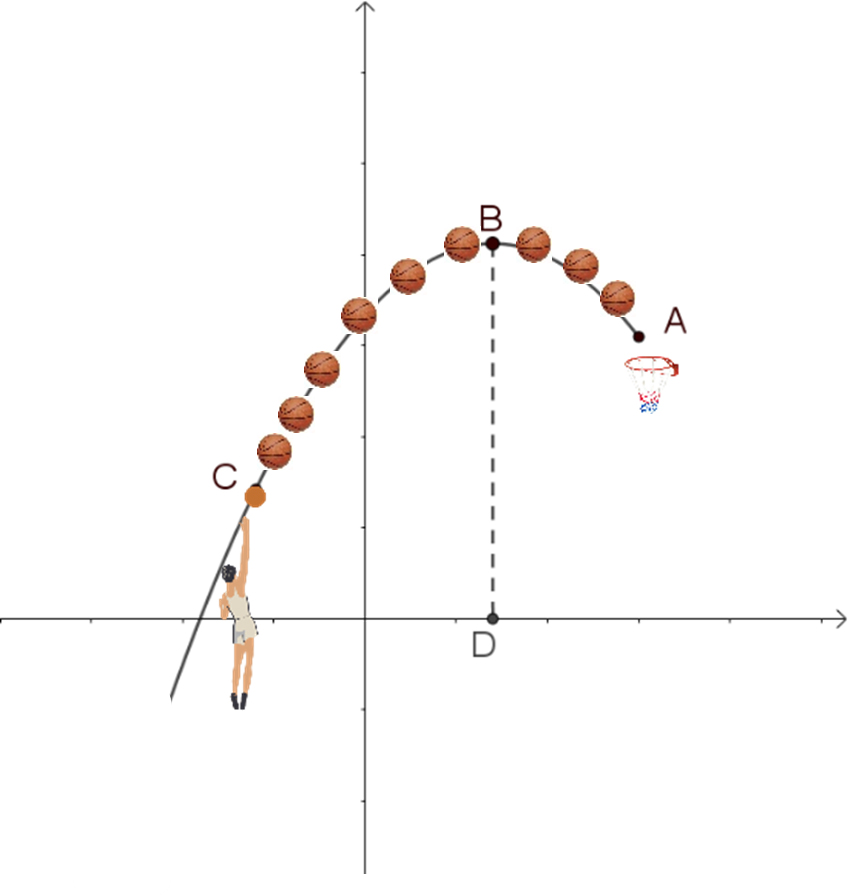
במערכת הצירים שבאיור א' מרכז הסל נמצא בנקודה A(6,32)A(6,32).
הנקודה B מייצגת את הנקודה הגבוהה ביותר אליה מגיע הכדור.
BD מאונך לציר ה- x ואורכו 41 יחידות אורך*.
בנוסף, מרחק הנקודה D מראשית הצירים הוא 3 יחידות אורך.
השחקן משחרר את הכדור בנקודה C.
מה יכולים להיות שיעורי הנקודה C על מנת שהכדור יכנס לסל?
* יחידות האורך אינן יחידות מידה סטנדרטיות (כמו למשל מטר, ס"מ).
איור א'
- אחרי שפתרתם את בעיית מטרה 1, המשיכו לבעיית מטרה 2.
- במידת הצורך, פתרו את השאלות במדרגה 1.
הצעת פתרון לבעיית מטרה 1
נשתמש בייצוג קודקודי של פרבולה: y=a(x−p)2+ky=a(x−p)2+k.
מהנתון נובע כי נקודת הקודקוד הינה מקסימום, לכן: a<0a<0 ושיעוריה: B(3,41)B(3,41).
לכן, משוואת הפרבולה היא מהצורה: y=a(x−3)2+41y=a(x−3)2+41.
נציב את הנקודה A(6,32)A(6,32) המייצגת את מיקום מרכז הסל ונקבל a=−1a=−1.
לכן, משוואת הפרבולה המתאימה היא: y=−(x−3)2+41y=−(x−3)2+41.
כל נקודה על הפרבולה עונה על הדרישה.
חשוב לשים לב כי האפשרויות המתאימות לנקודה C כך שהכדור יכנס לסל הן אלו ששיעורי ה- x שלהן קטנים מ- 3, אחרת זה לא הגיוני.
דוגמאות לנקודות שמהן ישחרר השחקן את הכדור והכדור ייכנס לסל:
C(−2,16)C(−2,16) ; C(−1,25)C(−1,25) ; C(0,32)C(0,32) ; C(1,37)C(1,37).
אפשר להציע לתלמידים להשתמש בתוכנה לסרטוט גרפים למשל Desmos ולהיעזר בה למציאת שיעורי הנקודות המתאימות.
מטרות בעיית מטרה 1
המטרות של בעיית המטרה הן:
- לקשר בין מתמטיקה לכדורסל.
- למצוא ייצוג אלגברי של פונקציה ריבועית על פי נקודות נתונות.
- למצוא הצגה פרמטרית של פונקציה ריבועית.
- להבין משמעות נקודת מקסימום.
- לחקור תפקיד של כל אחד מהפרמטרים בייצוגים שונים של פונקציה ריבועית.
בבעיית המטרה מתואר מצב בו נתון מיקום הסל וכן הנקודה הגבוהה ביותר אליה הוא מגיע (נקודת המקסימום של הפונקציה הריבועית). התלמידים מתבקשים למצוא אפשרויות שונות לשיעורי הנקודה שאם השחקן ישחרר ממנה את הכדור אז הכדור ייכנס לסל. התשובה יכולה להיות על ידי מתן דוגמאות או על ידי הכללה.

איור ג'
בעיה 1.1.1
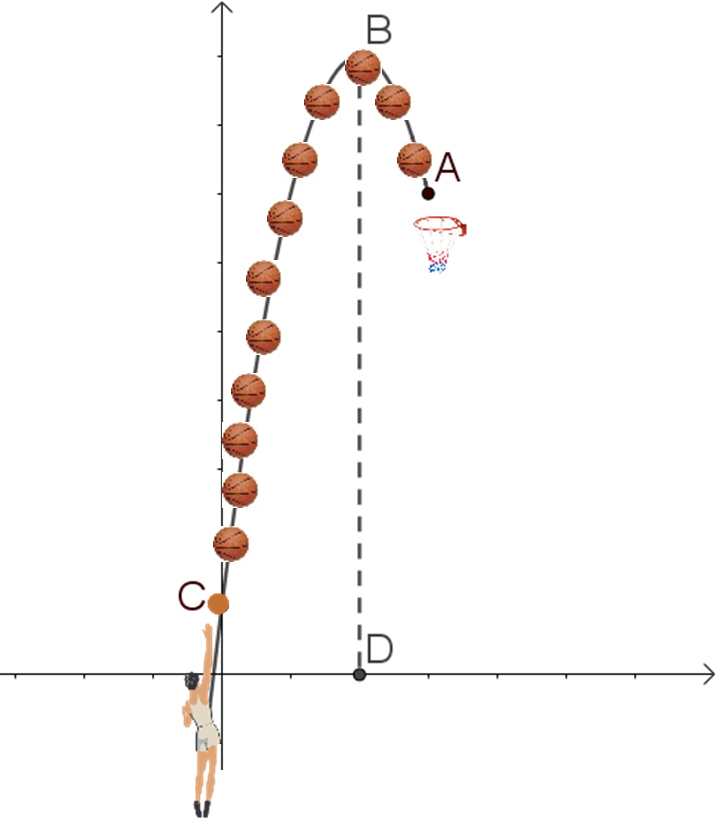
במערכת הצירים שבאיור ג' מרכז הסל נמצא בנקודה A(6,29)A(6,29).
הנקודה B מייצגת את הנקודה הגבוהה ביותר אליה מגיע הכדור.
BD מאונך לציר ה- x ואורכו 38 יחידות אורך.
בנוסף, מרחק הנקודה D מראשית הצירים הוא 3 יחידות אורך.
ידוע שהכדור נכנס לסל.
מהו הביטוי האלגברי שמייצג את הפרבולה המתאימה?
(ייצוג קודקודי של פרבולה הוא: y=a(x−p)2+ky=a(x−p)2+k)
ניתן להיעזר ביישומון.
- בחרו מתוך ערכי aa את הפונקציה הריבועית המייצגת את הפרבולה שעוברת דרך מיקום הסל.
- במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
הצעה לפתרון מדרגה 1 של בעיית מטרה 1
פתרון בעיה 1.1.1
בעיה זו דומה לבעיה המוצגת בבעיית מטרה 1. יש שינוי בשיעורי הנקודות, כך שאחרי שפותרים בעיה זו כדאי לחזור לבעיית המטרה ולפתור אותה.
היישומון המוצע הוא למעשה "המדרגה" ובעזרתו ניתן למצוא את הייצוג האלגברי המתאים.
ביישומון מסומנות הנקודות A(6,29)A(6,29) ו- B(3,38)B(3,38) ונתונה פרבולה מהצורה y=a(x−3)2+38y=a(x−3)2+38 עם סרגל הזזה עבור a.
התלמידים יכולים להזיז את סרגל ההזזה עד שיגיעו לביטוי של פרבולה שעוברת דרך הנקודה A. במקביל מוצג הביטוי האלגברי של הפרבולה.
משוואת הפרבולה המתאימה היא: y=−(x−3)2+38y=−(x−3)2+38.
כל נקודה על הפרבולה עונה על הדרישה.
חשוב לשים לב כי האפשרויות המתאימות לנקודה C כך שהכדור יכנס לסל הן אלו ששיעורי ה- x שלהן קטנים מ- 3, אחרת זה לא הגיוני.
נתון כי השחקן משחרר את הכדור בנקודה C(0,2)C(0,2) והסל נמצא בנקודה A(6,14)A(6,14).
מהו הגובה המקסימלי שאליו יכול להגיע הכדור?
תנו הצעות אפשריות נוספות לגובה שאליו הכדור יכול להגיע.
- במידת הצורך, פתרו את השאלות במדרגה 1.
איור ב'
הצעת פתרון לבעיית מטרה 2
בפתרון בעיה זו התלמידים יכולים לתת דוגמאות ולא חייבים לתת את הייצוג הפרמטרי של משפחת הפונקציות המתאימה. להלן נציג פתרון פרמטרי ודוגמאות.
נשתמש בייצוג סטנדרטי של פרבולה: y=ax2+bx+cy=ax2+bx+c.
מהנתון נובע כי נקודת הקודקוד הינה מקסימום, לכן: a<0a<0.
כמו כן, הנקודה C(0,2)C(0,2) נמצאת על גרף הפונקציה. לכן, הפונקציה היא מהצורה: f(x)=ax2+bx+2f(x)=ax2+bx+2.
נציב את הנקודה A(6,14)A(6,14) המייצגת את מיקום מרכז הסל ונקבל: f(x)=ax2+(2−6a)x+2f(x)=ax2+(2−6a)x+2.
זוהי משפחה של פונקציות שעוברות דרך שתי הנקודות הנתונות.
למציאת הגובה המקסימלי שאליו יכול להגיע הכדור נשתמש בנוסחה: yדוקדוק=4ac−b24ayדוקדוק=4ac−b24a
ונקבל: yדוקדוק=−9a−1a+8yדוקדוק=−9a−1a+8.
דוגמאות:
- עבור a=−1a=−1 נקבל כי הפונקציה המתאימה היא: y=−x2+8x+2 והגובה המקסימלי שאליו יגיע הכדור הוא 18 יחידות אורך.
- עבור a=−0.6 נקבל את הפונקציה: y=−0.6x2+5.6x+2 והגובה המקסימלי שאליו יגיע הכדור הוא 15.07 יחידות אורך.
חשוב לשים לב כי הערכים המתאימים עבור a הם: a<−13.
בנוסף, ערכי x האפשריים הם: 0<x<6 על מנת להבטיח שנקודה B תימצא בין הנקודות A ו- C.
כאשר a=−13 הסל נמצא בגובה המקסימלי, כלומר נקודות A ו- B מתלכדות.
כאשר −13<a<0 , הסל נמצא לפני הגובה המקסימלי. כלומר, נקודה A נמצאת בין הנקודות C ו- B וזה אינו מתאים לתיאור הסיטואציה.
הערה: אפשר לפתור גם על ידי שימוש בהצגה הקודקודית של הפונקציה הריבועית ואז מתקבלת משפחת הפונקציות:
f(x)=a(x−3+1a)2+2−a(3−1a)2
מטרות בעיית מטרה 2
המטרות של בעיית המטרה הן:
- לקשר בין מתמטיקה לכדורסל.
- למצוא ייצוג אלגברי של פונקציה ריבועית על פי נקודות נתונות.
- למצוא הצגה פרמטרית של פונקציה ריבועית.
- להבין משמעות נקודת מקסימום.
- לחקור תפקיד של כל אחד מהפרמטרים בייצוגים שונים של פונקציה ריבועית.
בבעיית המטרה נתונים שיעורי הנקודה שממנה משחרר השחקן את הכדור וכן שיעורי הנקודה שבה נמצא הסל. התלמידים מתבקשים למצוא אפשרויות שונות לגובה המקסימלי שאליו יכול להגיע הכדור. התשובה יכולה להיות על ידי מתן דוגמאות או על ידי הכללה.
איור ד'
בעיה 2.1.1
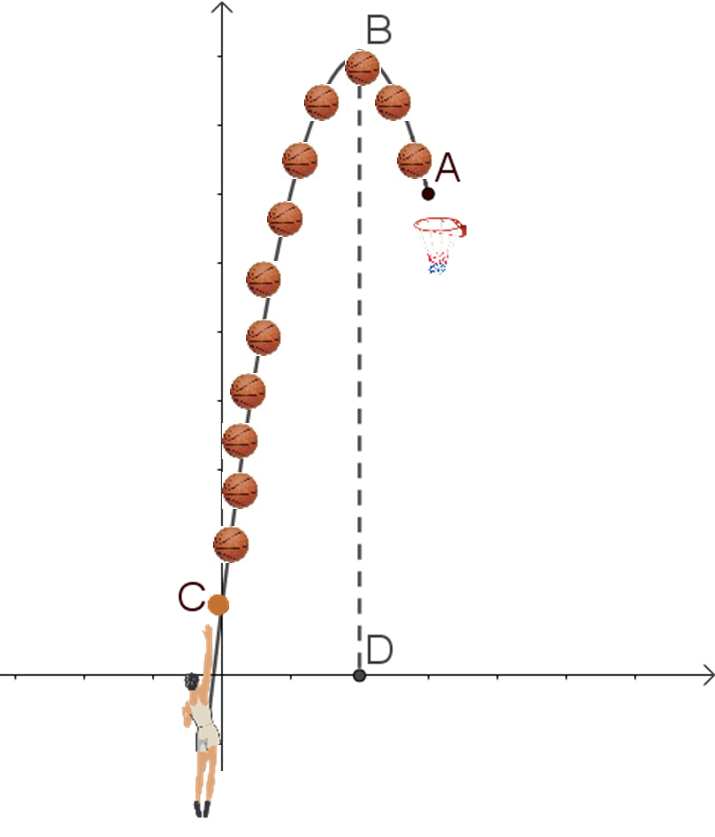
באיור מתואר מיקום כדור בזמנים שונים במהלך זריקה לסל.
נתון כי השחקן משחרר את הכדור בנקודה C(0,2) והסל נמצא בנקודה A(6,14).
הגובה המקסימלי שאליו מגיע הכדור הוא 18 יחידות אורך.
לפניכם ביטויים אלגבריים.
בחרו את הביטויים המתאימים לתיאור מסלול הכדור.
- y=−x2+8x+18
- y=−(x−6)(x−14)
- y=−(x−4)2+18
- y=−(x−6)2+14
- y=−x2+8x+2
ניתן להיעזר ביישומון.
- התאימו לכל אחד מהביטויים המוצעים, את התיאור הגרפי שמתאים לתיאור מסלול הכדור.
סמנו V בתיבת הבחירה ובדקו אם הנקודות הנתונות נמצאות על המסלול שבחרתם. - במידת הצורך, היעזרו בהנחיות כלליות נוספות לשימוש ביישומונים.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 2.
הצעה לפתרון מדרגה 1 של בעיית מטרה 2
פתרון בעיה 2.1.1
בעיה זו דומה לבעיה המוצגת בבעיית מטרה 2. אחרי שפותרים בעיה זו כדאי לחזור לבעיית המטרה ולפתור אותה.
היישומון המוצע הוא למעשה "המדרגה" ובעזרתו ניתן למצוא את הייצוג האלגברי המתאים.
כאן נתונות נקודות A(6,14) ו- C(0,2) ובשונה מאשר בבעיית המטרה נתון גם כי הגובה המקסימלי שאליו מגיע הכדור הוא 18 יחידות אורך.
ביישומון מסומנות הנקודות וגם מצוירת הפונקציה f(x)=18.
כמו כן מצויירות 5 פונקציות כאשר יש תיבת בחירה להראות את הגרף או להסתיר.
התלמידים יכולים לבחור כל אחד מהביטויים האלגבריים המוצגים ולבדוק האם מקיים את תנאי הבעיה. התשובות הנכונות נתונות בייצוגים שונים.
חשוב לבקש מהתלמידים לנמק את בחירתם הן במקרים הנכונים והן במקרים השגויים.
| מושגים | תשובה | דוגמה לנימוק | |
|---|---|---|---|
| א. | y=−x2+8x+18 | לא נכון | הנקודה C(0,2) לא מקיימת את הביטוי האלגברי. |
| ב. | y=−(x−6)(x−14) | לא נכון | הביטוי הנתון חותך את ציר ה-x בנקודות (6,0) , (14,0). |
| ג. | y=−(x−4)2+18 | נכון | הנקודות A ו- C מקיימות את הביטוי האלגברי ושיעור ה-y של נקודת המקסימום הוא 18. |
| ד. | y=−(x−6)2+14 | לא נכון | הנקודה C(0,2) לא מקיימת את הביטוי האלגברי. |
| ה. | y=−x2+8x+2 | נכון | הנקודות A ו- C מקיימות את הביטוי האלגברי ושיעור ה-y של נקודת המקסימום הוא 18. |










