אשכול כמה רחוק קו האופק?
בתאריך 24 באוקטובר 2014 אלן יוסטס (Robert Alan Eustace) סגן נשיא בכיר בחברת גוגל, קבע את שיא העולם לנפילה חופשית מגובה של כ-41 ק"מ.
אלן שבר את השיא הקודם שנקבע בתאריך 14 באוקטובר בשנת 2012 על ידי פליקס באומגרטנר האוסטרי, שצנח מגובה של כ- 38 ק"מ.
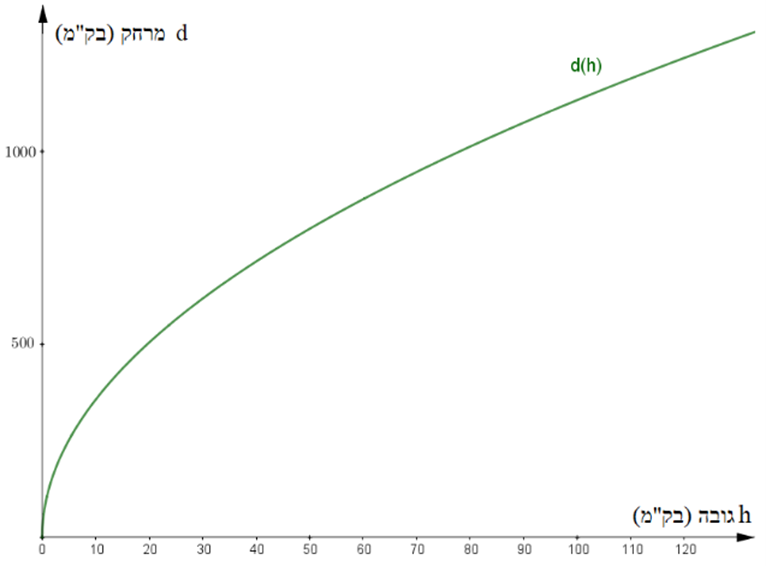
נתון גרף הפונקציה d(h) המתארת מרחקו של צופה אל קו האופק d (בק"מ), כפונקציה של גובה עין של הצופה h (בק"מ) מעל פני כדור הארץ.
- תארו לפחות שתי תכונות שונות של הפונקציה d(h) בהסתמך על הגרף.
כיצד תכונות אלה באות לידי ביטוי בחיי היומיום?
- סמנו על גרף הפונקציה שתי נקודות המתארות את שני השיאים של צניחה לעבר הקרקע.
שערו בכמה רחוק יותר (בערך) המרחק שראה אלן יוסטס את קו האופק, מאשר המרחק שראה פליקס באומגרטנר את קו האופק.
בדקו את תשובתכם ביישומון.
- באיזה גובה צריך להיות צופה, כדי לראות את קו האופק במרחק של כ-1,000 ק"מ?
בדקו את החישובים שלכם ביישומון.
- אילו שאלות נוספות אפשר לשאול ?
תוכלו לקרוא את הכתבה "נגע בשמיים: שיא חדש לקפיצה מקצה החלל", שפורסמה באתר ynet בתאריך 25.10.14.
בחלון הימני:
- לחיצה על הכפתורים "מגדל" או "תחנת חלל" מדגימה את הגובה של הצופה, ומשנה בהתאם, בחלון השמאלי, את:
- הערכים בסרגל הגרירה
- הנקודה שעל הפונקציה
- לחיצה על "הגדלה/הקטנה" מציגה את פני הכדור בהתאם.
בחלון השמאלי:
- סמנו את d(h) כדי להציג את פונקציית המרחק.
- גררו את הנקודה בסרגל הגרירה, כדי לראות ערכים שונים של h ו-d.
- בתמונה המוגדלת בפינה העליונה, תוכלו לראות בהגדלה את ההצגה של פני הכדור שבחלון הימני.
- ניתן לנקות עקבות שנוצרו עקב גרירת הנקודה על הפונקציה.
- במידת הצורך, פתרו את השאלות במדרגה 1.