אשכול מראות פרבוליות - מוקד, מדריך ומה שביניהם - חלק ב - הקדמה - למורה
מבנה האשכול
יישומונים
مبنى العنقود
הנחיות למורה
אשכול 2 מתוך 3 אשכולות.
הערה: אם בכיתה פתרו את בעיית מטרה 2 – סיכום (בעיית רשות) שבאשכול א, אז ניתן לדלג על אשכול זה ולעבור לאשכול: "מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק ג"
יחידה:
מדע – מתמטיקה
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
30-45 דקות
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| פרבולה | – מוקד – מדריך – מרחק בין שתי נקודות – מרחק בין נקודה לישר | – יישום תכונה של פרבולה: כל נקודה על הפרבולה נמצאת במרחק שווה ממוקד הפרבולה ומהמדריך. |
| פרבולה | – ביטוי אלגברי של פרבולה. | – מציאת ביטוי אלגברי של פרבולה, על פי נקודה על הפרבולה וגרף הפרבולה. |
| משפט פיתגורס | – משולש ישר זווית – ניצב – יתר | – יישום המשפט במערכת צירים לצורך פתירת בעיה. |
מטרת האשכול:
יישום וביסוס תכונה של הפרבולה: כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה. יישום תכונה זו הוא לצורך פתרון בעיה במציאות, הקשורה למראות פרבוליות – אליה נתייחס באשכול השלישי.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
- מוקד של פרבולה
- מדריך של פרבולה
- כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה.
שלב הלמידה המומלץ:
לאחר הכרת הפרבולה ותכונותיה.
מערך דידקטי מומלץ:
ארגון הכיתה:
- חזרה במליאה על המושגים מוקד ומדריך ועל התכונה של פרבולה בהקשר זה, שנלמדו באשכול – חלק א.
- ארגון הכיתה בקבוצות של 2-4 תלמידים.
- תלמידים פותרים את בעיית מטרה 1, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול וביישומונים.
- דיון כיתתי בו תלמידים מציגים את תשובותיהם ומסבירים אותן.
- תלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
שאלות מומלצות לדיון כיתתי:
- באילו קשיים נתקלתם בפתרון בעיית המטרה?
- כיצד עזרו המדרגות בהתמודדות עם הקשיים בהם נתקלתם?
- כיצד עזרו היישומונים בהתמודדות עם הקשיים בהם נתקלתם?
אשכול מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק ב – הקדמה
למדנו כי:
הגרף המתקבל מאוסף כל הנקודות, שמרחקן מנקודה F, שווה למרחקן מישר m, הוא פרבולה.
נקודה F נקראת מוקד הפרבולה. ישר m נקרא מדריך הפרבולה.
לפרבולה המוכרת לנו, תכונה נוספת:
מרחקה של כל נקודה על הפרבולה, ממוקד הפרבולה, שווה למרחקה ממדריך הפרבולה.
ראו יישומון מצורף.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
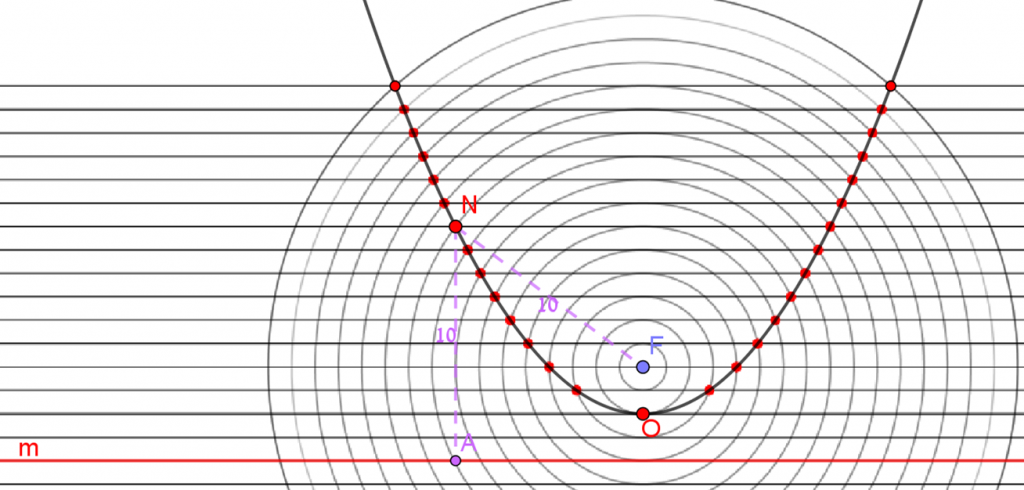
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.
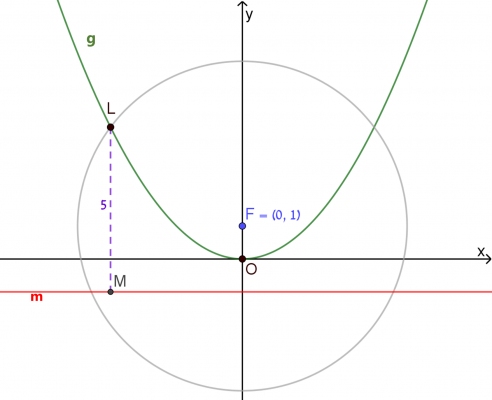
מצאו את:
- שיעורי נקודה L.
- הביטוי האלגברי של הפרבולה.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
פתרון בעיית מטרה 1
א. מציאת שיעורי נקודה L:
המדריך, הישר m, מקביל לציר ה- x.
בניית עזר קטע AF כך ש:
\(MC||BO||AF\)
נקודה L על הפרבולה, לכן מרחקה מהמוקד F, שווה למרחקה מהמדריך, הישר m.
\(LF=LM=5\)
נקודה O על הפרבולה, לכן מרחקה מהמוקד F, שווה למרחקה מהמדריך, הישר m.
\(FO=CO=1\)
\(LM \perp MC\) מרחק נקודה מישר הוא אורך האנך מהנקודה לישר.
\(BM=CO=1\) מרחקים שווים בין ישרים מקבילים
\(BA=FO=1\)
\(LA=5-2=3\)
\(LA \perp AF\)
\(AF^2=LF^2-LA^2\) משפט פיתגורס
\(AF=\sqrt{25-9}=4\)
שיעורי נקודה \(L(-4,4)\)
\(\space\)
ב. מציאת ביטוי אלגברי לפרבולה:
\(y=a\cdot x^2\)
\(4=a\cdot 16\)
\(y=0.25\cdot x^2\)
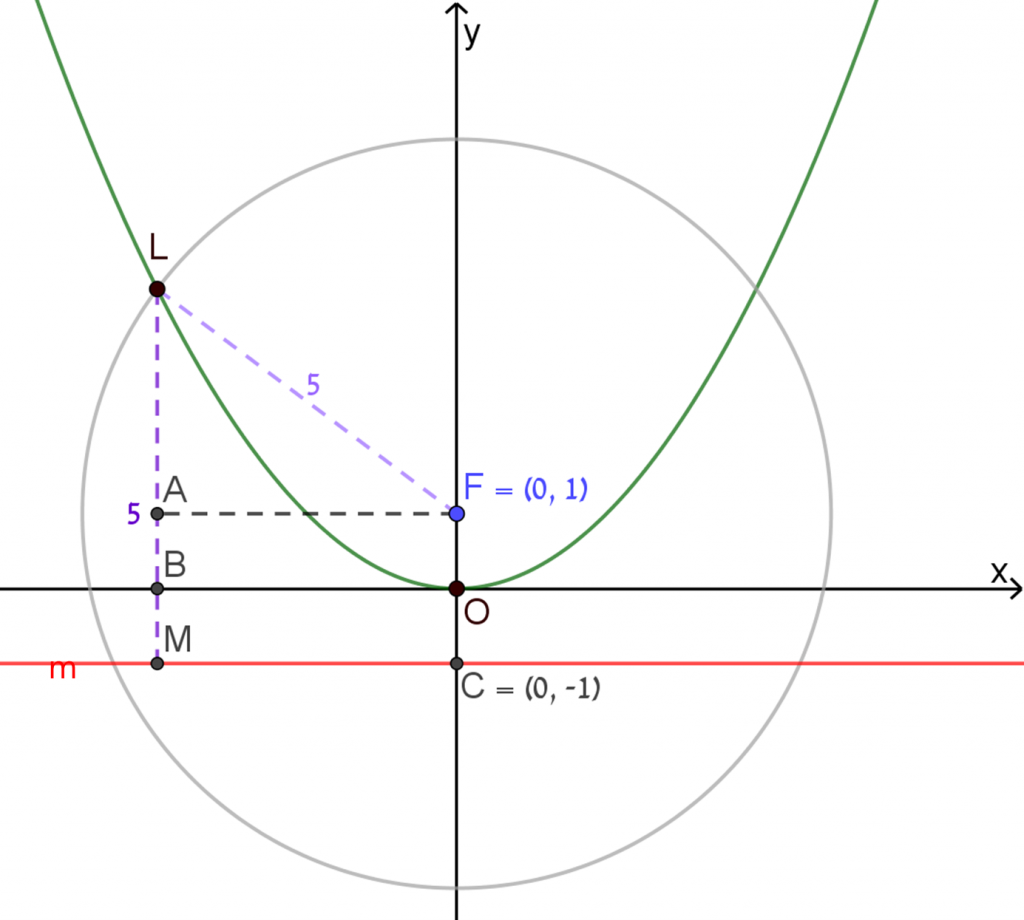
מצאו את:
- הביטוי האלגברי למדריך הפרבולה.
- אורך הקטע FC.
- שטח משולש FCR.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
א. ביטוי אלגברי של המדריך לפרבולה:
\(y=-2\)
\(\space\)
ב. אורך הקטע FC
\(CA\perp m\)
\(FC=CA=4.5+2=6.5\)
\(\space\)
ג. שטח משולש FCR
\(RF=4.5-2=2.5\)
\(RC=\sqrt{6.5^2-2.5^2}=6\)
שטח משולש FCR הוא:
\(\Large\frac{2.5\cdot 6}{2}\normalsize=7.5\)
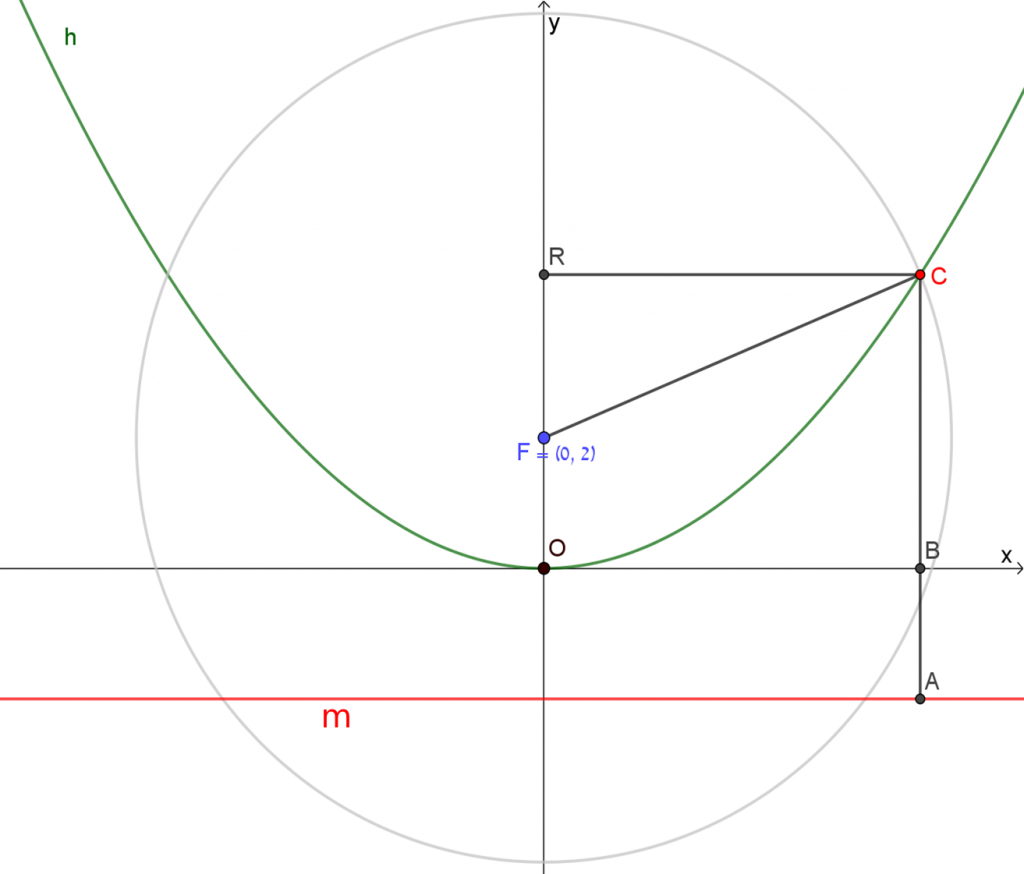
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
בסרטוט המצורף לבעיית המדרגה, מופיע משולש ישר זווית.
מכך ניתן להבין כי בבעיית המטרה יש להוסיף לסרטוט קטעים, כך שייווצר משולש ישר זווית, בדומה לבעיית המדרגה.
בבעיית המדרגה מתבקשים למצוא את הביטוי האלגברי למדריך הפרבולה.
לצורך פתרון בעיית המטרה יש למצוא את הביטוי האלגברי למדריך, למרות שלא מתבקשים למצוא זאת במפורש.
בבעיית המדרגה מתבקשים למצוא את שטח המשולש.
לשם כך יש להיעזר במשפט פיתגורס.
וזו תזכורת לכך שגם בבעיית המטרה יש להיעזר במשפט פיתגורס.
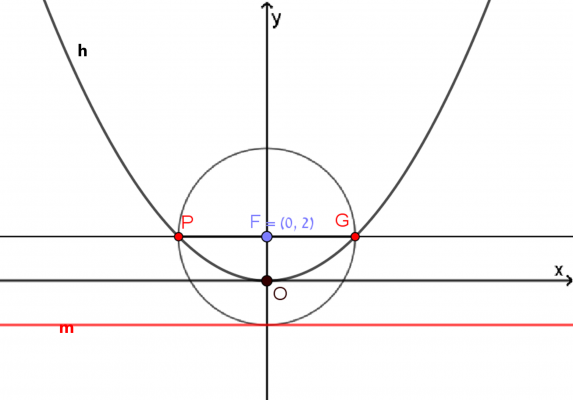
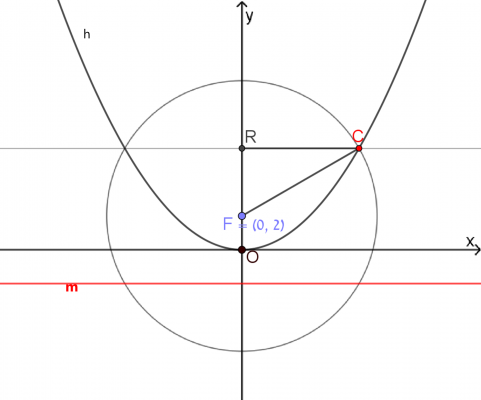
מצאו את:
- הביטוי האלגברי של מדריך הפרבולה.
- שיעורי נקודה P.
- הביטוי האלגברי של הפרבולה.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
א. ביטוי אלגברי של המדריך m:
\(Y=-2\)
\(\space\)
ב. שיעורי נקודה P:
\(PE\perp m\)
\(PE=PS+SE=2+2=4\)
\(PF=PE=4\)
שיעורי נקודה P הם: \((-4,2)\)
\(\space\)
ג. מציאת ביטוי אלגברי לפרבולה:
\(y=a⋅x^2\)
\(2=a\cdot 16\)
\(y=0.125\cdot x^2\)
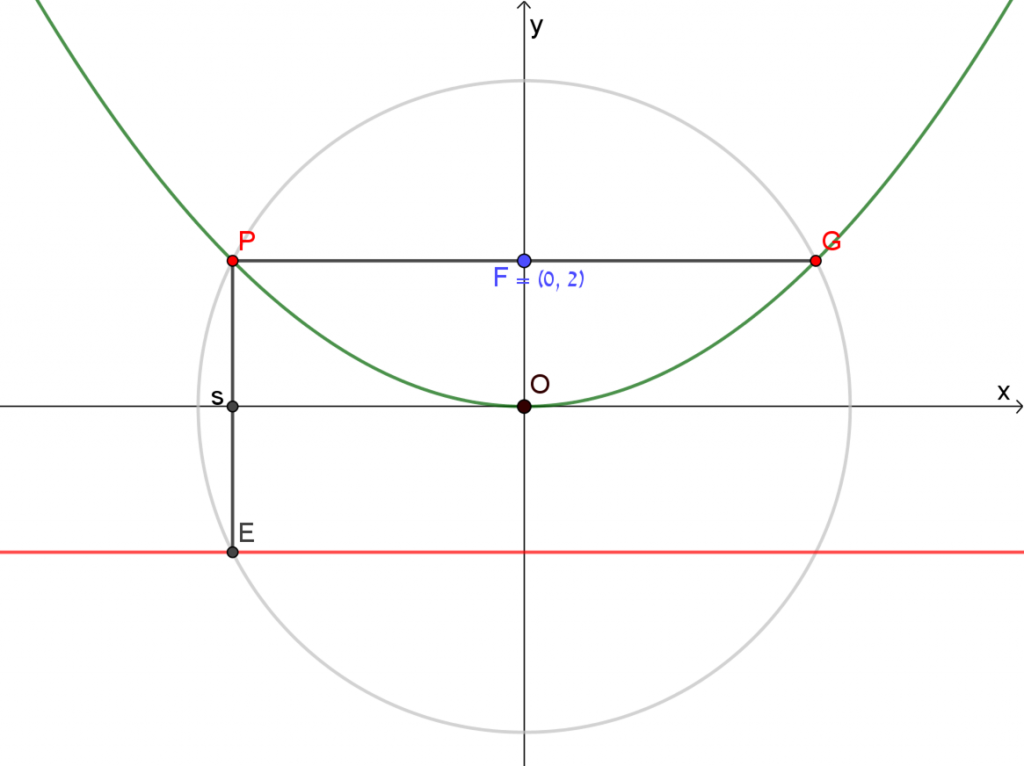
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
הבעיה במדרגה 2 פשוטה יותר מהבעיה במדרגה 1.
בבעיה זו מתבקשים למצוא את הביטוי למדריך הפרבולה ויש להיעזר בתכונה של הפרבולה:
כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה ומהמדריך.
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.