אשכול דמיון בעדשות חלק ב - הכללה - למורה
יישומונים
הנחיות למורה
אשכול 2 מתוך 3 אשכולות.
יחידה:
מדע – אופטיקה
כיתה מומלצת:
כיתה ח / כיתה ט / כיתה י
משך הזמן המומלץ:
45-90 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
עדשה מרכזת, מוקד עדשה, מהלך קרני אור העוברים דרך עדשה מרכזת, דמות אופטית וסרטוטה, דמות ממשית.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| דמיון משולשים | – משולשים דומים – יחס בין צלעות משולשים – פרופורציה | – זיהוי משולשים דומים שבהם לכל זווית במשולש אחד, יש זווית ששווה לה במשולש אחר. – מציאת יחס בין צלעות מתאימות במשולשים דומים. – מציאת נתונים חסרים מתוך תכונות הדמיון ותוך שימוש בפרופורציה. |
| הכללה של ביטויים מספריים | – הכללה – חוקיות – סדר גודל | – מציאת חוקיות בשילוב שברים ותכנים גאומטריים. |
| חפיפת משולשים | – משפטי חפיפה | – זיהוי משולשים חופפים. – הוכחת חפיפת משולשים. – הסקת מסקנות לגבי זוויות שוות במשולשים חופפים. |
| ישרים מקבילים | – זוויות מתאימות | – זיהוי זוויות מתאימות. – הוכחה שישרים מקבילים. |
| בעיות אורייניות מתוך מציאות קרובה לתלמידים | – עדשה מרכזת – מוקד – דמות אופטית | – פתרון בעיות המשלבות בין הבנת טקסט מילולי, המסביר את מהלך קרני האור העובר דרך עדשה מרכזת, לבין הידע המתמטי של תלמידים, בנושא דמיון משולשים. |
מטרת האשכול:
ידע מתמטי של דמיון משולשים, מאפשר להבין במה תלוי היחס בין גודל העצם לגודל הדמות של העצם, המשתקפת דרך עדשה מרכזת, ולחשב יחס זה.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
העמקה בנושא דמיון משולשים.
שלב הלמידה המומלץ:
בכיתה ח – סיכום של נושא דמיון משולשים.
בכיתה ט – לקראת סוף השנה, כחזרה וכהכנה לכיתה י'.
מערך דידקטי מומלץ:
ארגון הכיתה:
- ניתן לפתוח את השיעור בשאלות לגבי מה שנלמד באשכול "דמיון בעדשות – חלק א".
- ארגון הכיתה בקבוצות של 2-4 תלמידים.
- התלמידים יקראו את תיאור הסיטואציה.
- תלמידים פותרים את בעיות המטרה, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול.
- דיון כיתתי בו התלמידים מציגים את תשובותיהם ומסבירים אותן.
- התלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
שאלות מומלצות לדיון כיתתי:
- במה עוזרת לנו המתמטיקה כדי להבין את המציאות, בהקשר לאשכול זה?
אשכול דמיון בעדשות חלק ב – הכללה
באשכול הקודם "דמיון בעדשות – חלק א", למדנו:
- מה זו עדשה דו קמורה
- על המוקדים בעדשה קמורה (F,F1)(F,F1),
ועל מרחק המוקדים ממרכז העדשה: OF=OF1=fOF=OF1=f - על מהלך קרני האור העוברות דרך עדשה קמורה
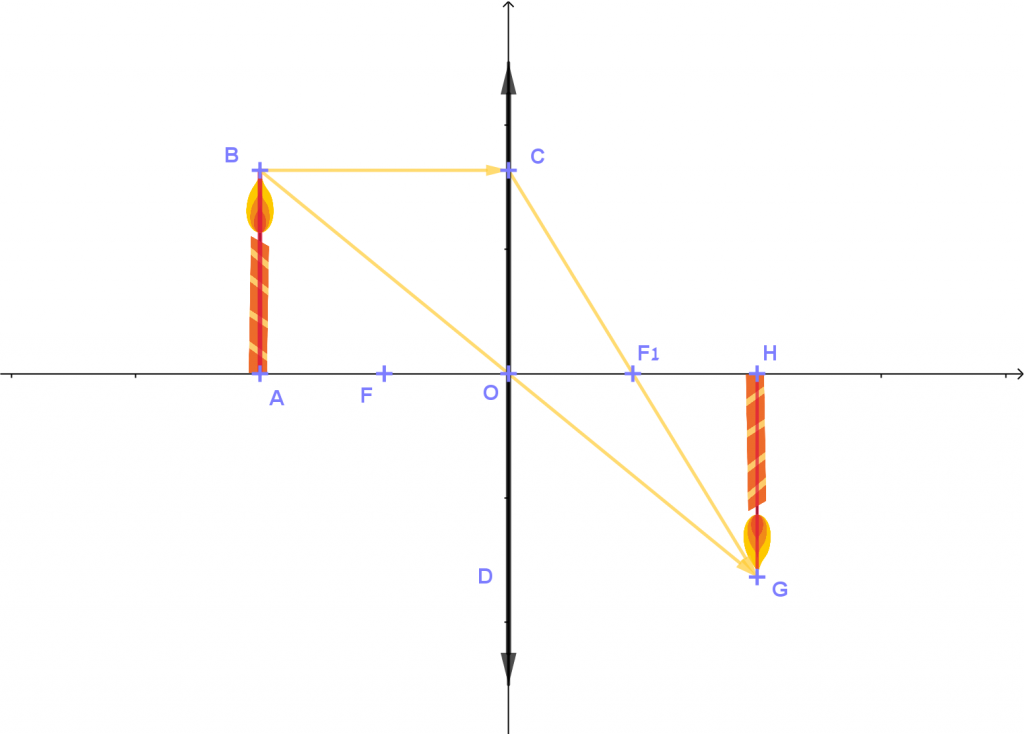
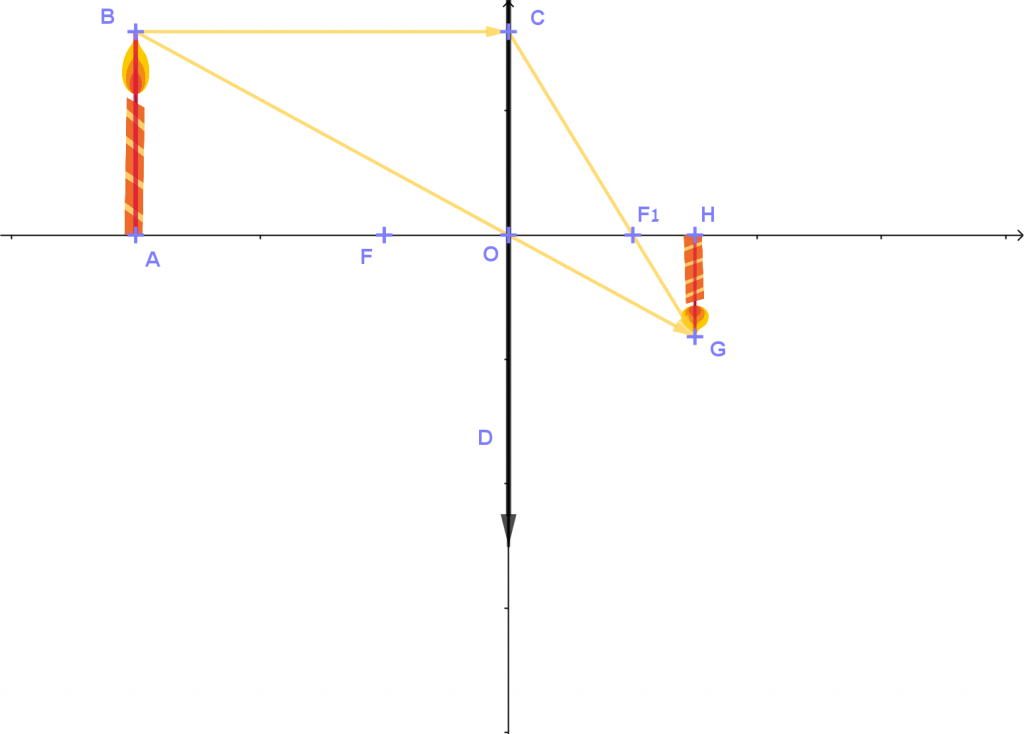
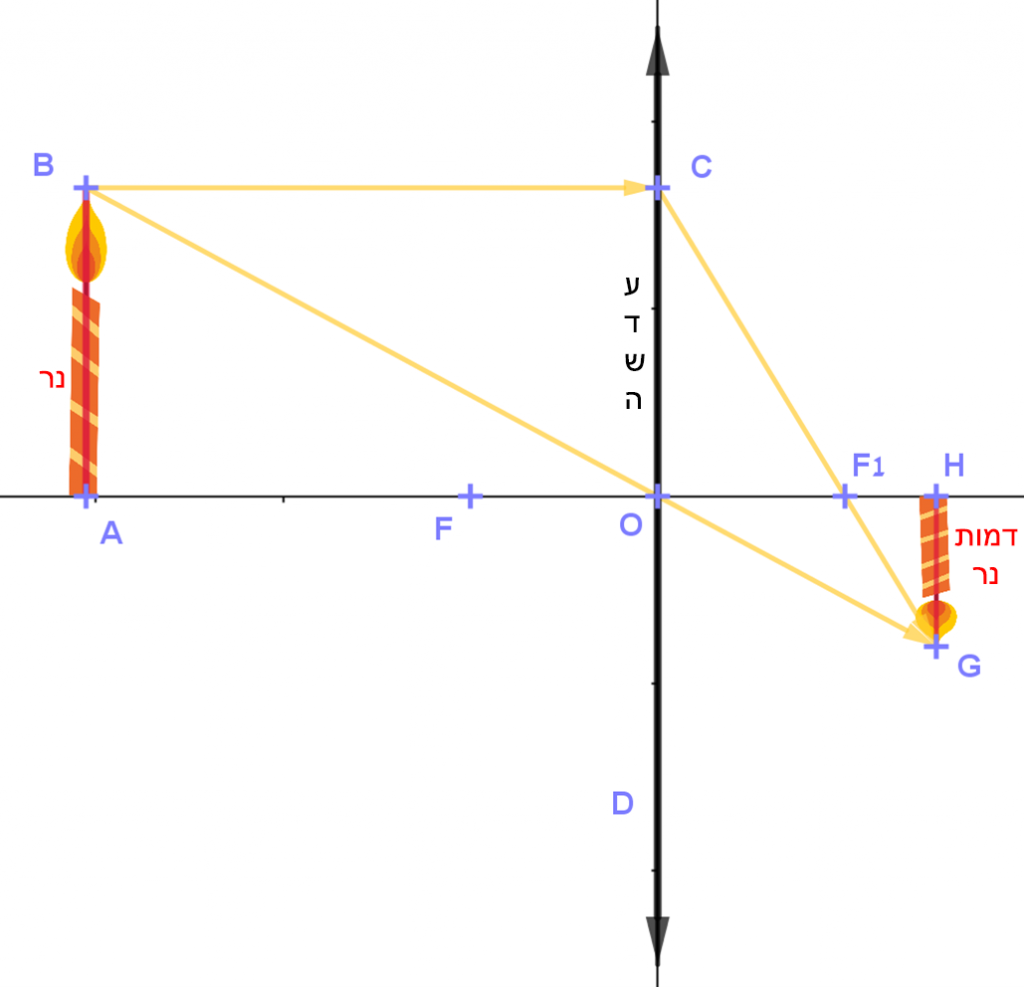
- על סרטוט הדמות האופטית של נר (HG) המשתקף דרך עדשה קמורה (ראו סרטוט מצורף)
- כאשר AO>fAO>f, הדמות האופטית היא ממשית והפוכה.
גודלה יכול להיות קטן מגודל מהנר, גדול מהנר או שווה לו.
באשכול זה נבדוק במה תלוי גודל הדמות האופטית, כאשר AO>fAO>f.
1. בעיית מטרה 1 – הכללה
באשכול "דמיון בעדשות – חלק א", הוכח כי כאשר AO>fAO>f, מתקיים ש:
ABHG=COHG=OF1HF1ABHG=COHG=OF1HF1
ABHG=AOOHABHG=AOOH
- היעזרו במה שהוכח והשלימו את הטבלה. נמקו תשובותיכם.
תוכלו להיעזר ביישומון המצורף.
מרחק המוקד ממרכז העדשה ff מרחק הנר ממרכז העדשה AOAO מרחק הדמות ממרכז העדשה HOHO AOf=kAOf=k היחס בין גודל הנר לגודל דמות הנר ABHGABHG 2 ס"מ 8 ס"מ 8/3 ס"מ 4 3 2 ס"מ 6 ס"מ חשבו חשבו חשבו 2 ס"מ 4 ס"מ 4 ס"מ 2 1 2 ס"מ 3 ס"מ 6 ס"מ 1.5 0.5 2 ס"מ 2.5 ס"מ חשבו חשבו חשבו הכללה ff AOAO ———— השלימו השלימו - הסיקו מסקנות מהטבלה, כאשר AO>fAO>f:
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר גדול יותר מאורך דמות הנר?
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר שווה בגודלו לאורך דמות הנר?
- עבור אילו ערכים של kk (AOf=k)(AOf=k), אורך הנר קטן יותר מאורך דמות הנר?
נמקו תשובותיכם.
תוכלו להיעזר ביישומון המצורף.
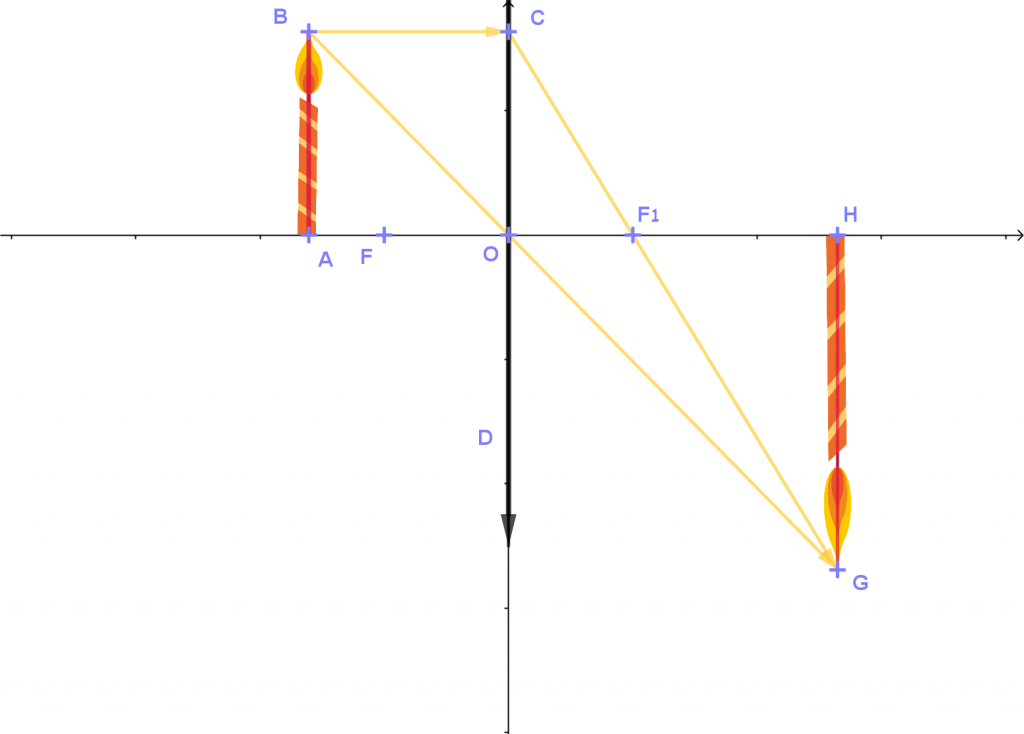
- מה ניתן להסיק לגבי הדמות כאשר k=1k=1?
סרטטו סרטוט מתאים והוכיחו תשובתכם בדרך גאומטרית.
תוכלו להיעזר ביישומון המצורף.
- אחרי שפתרתם את בעיית מטרה 1, המשיכו למה עוד אפשר לשאול.
- או, במידת הצורך, פתרו את השאלות במדרגה 1.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון בעיית מטרה 1
-
מרחק המוקד ממרכז העדשה ff מרחק הנר ממרכז העדשה AOAO מרחק הדמות ממרכז העדשה HOHO AOf=kAOf=k היחס בין גודל הנר לגודל דמות הנר ABHGABHG 2 ס"מ 8 ס"מ 8/3 ס"מ 4 3 2 ס"מ 6 ס"מ 3 ס"מ 3 2 2 ס"מ 4 ס"מ 4 ס"מ 2 1 2 ס"מ 3 ס"מ 6 ס"מ 1.5 0.5 2 ס"מ 2.5 ס"מ 10 ס"מ 1.25 0.25 הכללה ∗∗ ff AOAO ———— kk k−1k−1 - מצאנו כי ABHG=k−1ABHG=k−1
- אם k−1>1k−1>1, כלומר k>2k>2, אז ABHG>1ABHG>1.
עבור k>2k>2, אורך הנר גדול יותר מאורך דמות הנר.
- אם k−1=1k−1=1, כלומר k=2k=2, אז ABHG=1ABHG=1.
עבור k=2k=2, אורך הנר שווה לאורך דמות הנר.
- אם 0<k−1<10<k−1<1, כלומר 1<k<21<k<2, אז 0<ABHG<10<ABHG<1.
עבור 1<k<21<k<2, אורך הנר קטן יותר מאורך דמות הנר.

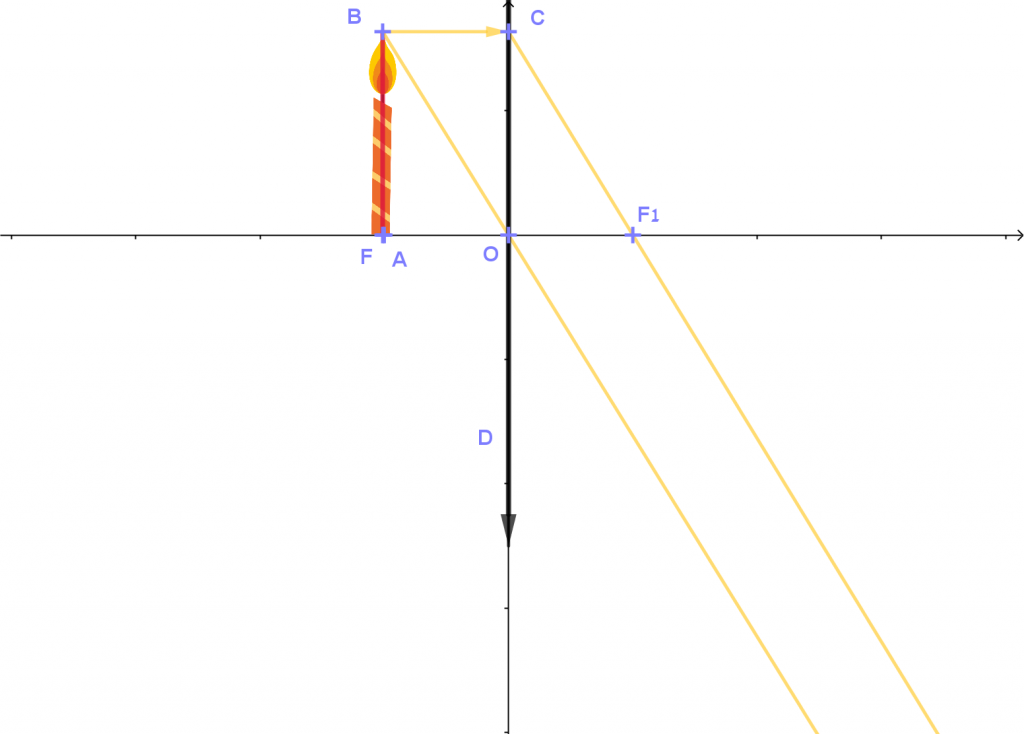
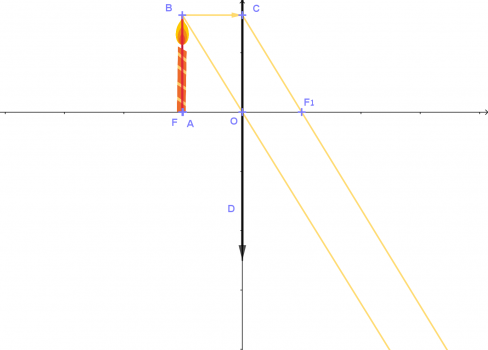
- כאשר k=1k=1, מרחק הנר ממרכז העדשה, שווה למרחק המוקד ממרכז העדשה.
מהלך הקרניים מתואר בסרטוט משמאל.
נתון כי: AO=OF1AO=OF1 (נקודות A ו- F מתלכדות)
יש להוכיח כי קרניים CF1CF1 ו- BOBO מקבילות ולכן לא נוצרת דמות.
הוכחה:
△BAO≅△COF1△BAO≅△COF1 משפט חפיפה צ.ז.צ
ניתן להסיק כי:
∡BOA=∡CF1O∡BOA=∡CF1O
ומכאן
CF1||OBCF1||OB
אפשרות נוספת היא להוכיח כי מרובע BCF1OBCF1O הוא מקבילית.
* הערה: יש לציין שההכללה אליה מגיעים על פי החוקיות המתגלה בטבלה, היא בגדר השערה, כיוון שהתלמיד לא נדרש להוכחה כללית.
תלמידים מתקדמים יכולים להגיע להוכחה כללית:
הוכחה כללית עם פרמטרים לסעיף א
נתון כי: AB⊥HAAB⊥HA
HG⊥AHHG⊥AH
BC∥AHBC∥AH
OF=OF1=fOF=OF1=f
AO=k⋅fAO=k⋅f
יש לבטא את: HO , ABHGHO , ABHG
פתרון:
△COF1∼△GHF1△COF1∼△GHF1 על פי משפט דמיון ז.ז.
⇓⇓
COHG=OF1HF1COHG=OF1HF1
מרובע ABCO הוא מלבן
(או חפיפת משולשים BCO ו- OAB)
⇓⇓
CO=ABCO=AB
⇓⇓
ABHG=OF1HF1=fHO−fABHG=OF1HF1=fHO−f
△BAO∼△GHO△BAO∼△GHO על פי משפט דמיון ז.ז.
⇓⇓
ABHG=OAOH=k⋅fOHABHG=OAOH=k⋅fOH
⇓⇓
ABHG=fHO−f=k⋅fOHABHG=fHO−f=k⋅fOH

(המשך פתרון)
⇓⇓
1HO−f=kOH1HO−f=kOH
⇓⇓
HO=k⋅HO−k⋅fHO=k⋅HO−k⋅f
⇓⇓
(k−1)HO=k⋅f(k−1)HO=k⋅f
⇓⇓
HO=k⋅fk−1HO=k⋅fk−1
⇓⇓
ABHG=OAOH=k⋅f(k⋅fk−1)=k−1ABHG=OAOH=k⋅f(k⋅fk−1)=k−1
1.1 מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
באשכול "דמיון בעדשות – חלק א", למדנו כי:
OF=OF1=fOF=OF1=f
וכאשר AO>fAO>f, מתקיים ש:
ABHG=COHG=OF1HF1ABHG=COHG=OF1HF1
ABHG=AOOHABHG=AOOH
אילו טענות מהטענות הבאות נכונות?
אם הטענה נכונה-נמקו, אם לא, תקנו את הטענה כך שתהיה נכונה.
תוכלו להיעזר ביישומון המצורף.
- AOOH=OF1HF1AOOH=OF1HF1
- אם ABHG>1ABHG>1, אז OH>AOOH>AO
- OH>OF
- f=OH−OF1
- אם AOf=k ו- k>1, אז אורך הנר גדול יותר מאורך דמות הנר.
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
| טענה | נכון/לא נכון | תיקון |
|---|---|---|
| א. AOOH=OF1HF1 | נכון, נובע מהפרופורציות שנלמדו באשכול חלק א | |
| ב. אם ABHG>1, אז OH>AO | לא נכון | אם ABHG>1, אז OH<AO |
| ג. OH>OF | נכון | |
| ד. f=OH−OF1 | לא נכון | f=OH−HF1 |
| ה. אם AOf=k ו- k>1, אז אורך הנר גדול יותר מאורך דמות הנר. | לא נכון | אם AOf=k ו- k>1, היחס בין אורך הנר לאורך דמות הנר משתנה. אורך הנר יכול להיות גדול מאורך דמות הנר, שווה לאורך דמות הנר, או קטן מאורך דמות הנר. |
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
הבעיה עוזרת לתלמיד להבחין בקשרים הקיימים בין קטעים שונים בסרטוט.
יש להיעזר בקשרים אלו כדי להגיע לחישובים המתאימים ולמלא את הטבלה וכן כדי להגיע להכללות ולענות על בעיה 1.2 בבעיית מטרה 1.
בעיה 1.2.2
הנר בסרטוט מאונך לציר העדשה AF1.
מרחק הנר ממרכז העדשה (AO) שווה למרחק המוקד ממרכז העדשה (f).
קרן האור BC מקבילה לציר העדשה.
מצאו בסרטוט צלעות שוות והוכיחו תשובתכם.
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
הבעיה עוזרת לתלמיד להבחין במצבים שונים המתייחסים ליחס בין גודל העצם, לגודל הדמות ולקשר בין יחס זה למרחק העצם ממרכז העדשה.
כמו כן, הבעיה גם עוזרת לתלמיד להבחין בקשרים הקיימים בין קטעים שונים בסרטוט, במצבים שונים של מרחק העצם ממרכז העדשה.
יש להיעזר בקשרים אלו כדי להגיע לחישובים המתאימים ולמלא את הטבלה וכן כדי להגיע להכללות ולענות על בעיה 1.2 בבעיית מטרה 1.
בעיה 1.2.2
הבעיה עוזרת לתלמיד להבין באיזה מצב לא נוצרת דמות.
וכן גם עוזרת לתלמיד להבין שכדי להוכיח שהקרניים מקבילות, עליו למצוא קטעים שווים בסרטוט ולשם כך יש להיעזר בחפיפת משולשים.
- ניתן לשנות את מיקום הנר, על-ידי גרירת נקודה A ימינה ושמאלה.
- ניתן לשנות את גובה הנר, על-ידי גרירת נקודה B למעלה ולמטה.
- ניתן לסמן משולשים שונים, על-ידי בחירת צבע המשולש בתפריט, ובחירת 3 קודקודים.