אשכול מראות פרבוליות - מוקד, מדריך ומה שביניהם - חלק א - הקדמה - למורה
הנחיות למורה
אשכול 1 מתוך 3 אשכולות.
יחידה:
מדע – מתמטיקה
כיתה מומלצת:
כיתה ט
משך הזמן המומלץ:
45 דקות
נושאים/מושגים חוץ מתמטיים הנלמדים באשכול (הֶקְשֶר):
נושאים חוץ מתמטיים הקשורים לאשכול זה, מופיעים בחלק ג.
ידע ומיומנויות מתמטיים נדרשים:
| נושא | מושגים | מיומנויות |
|---|---|---|
| מעגל | – מרכז מעגל. – רדיוס של מעגל. | – סימון נקודות על מעגל. |
| ישרים מקבילים | – מרחקים שווים בין ישרים. | – סימון נקודות על ישרים. |
| מרחק | – מרחק בין שתי נקודות. – מרחק בין נקודה וישר. | – סימון נקודות הנמצאות במרחק שווה מנקודה נתונה ומישר נתון. |
| פונקציה ריבועית ופרבולה | – ביטוי אלגברי של פונקציה ריבועית. – גרף של פרבולה. | – זיהוי גרף של פרבולה. – זיהוי ביטוי אלגברי של פונקציה ריבועית. |
| משפט פיתגורס (בעיית הרשות) | – משפט פיתגורס בשילוב שיעורי נקודות וקטעים במערכת צירים. |
מטרת האשכול:
הכרת תכונה של הפרבולה: כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה. יישום תכונה זו הינו לצורך פתרון בעיה במציאות, העוסקת במראות פרבוליות – אליה נתייחס באשכול השלישי.
ידע ומיומנויות מתמטיים נלמדים (חדשים):
- מוקד של פרבולה
- מדריך של פרבולה
- כל נקודה על הפרבולה נמצאת במרחקים שווים ממוקד הפרבולה וממדריך הפרבולה.
שלב הלמידה המומלץ:
לאחר הכרת הפרבולה ותכונותיה.
הערה:
בעיית הסיכום באשכול זה היא בעיית רשות. המורה יחליט אם תלמידים בכיתתו יפתרו בעיה זו.
תלמידים שפתרו את הבעיה יכולים לדלג על חלק ב' ולעבור לאשכול "מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק ג".
רצוי שתלמידים שלא פתרו בעיה זו, יעברו לאשכול "מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק ב".
מערך דידקטי מומלץ:
ארגון הכיתה:
- ארגון הכיתה בקבוצות של 2-4 תלמידים.
- תלמידים פותרים את בעיית מטרה 1, כאשר כל קבוצה, במידת הצורך, נעזרת במדרגות שבאשכול וביישומונים.
- דיון כיתתי בו תלמידים מציגים את תשובותיהם ומסבירים אותן.
- תלמידים פותרים את בעיית הסיכום. (זו בעיית רשות והמורה יחליט אם לבקש מהתלמידים לפתור אותה).
- המשך דיון כיתתי בבעיית הסיכום.
- תלמידים מעלים שאלות נוספות. המורה יכול לבחור שאלה אחת או יותר מתוך שאלות אלו ולפתח דיון עליהן.
- סיכום השיעור כפי שמובא באשכול. רצוי להציג ולהדגים את תכונת הפרבולה בעזרת היישומון המצורף.
שאלות מומלצות לדיון כיתתי:
- כיצד זיהיתם היכן לסמן את הנקודות המבוקשות?
- כיצד עזרו לכם המעגלים והקווים האופקיים למציאת הנקודות שיש לסמנן?
- מה ההגדרה של מרחק בין נקודה לישר?
- מהי ההגדרה של מעגל?
- האם נתקלתם בקשיים? אם כן, מה היו הקשיים?
- האם המדרגות ענו על הקשיים בהם נתקלתם?
- כיצד נעזרתם ביישומונים?
- מה לדעתכם יקרה אם המדריך יהיה מעל המוקד?
אשכול מראות פרבוליות – מוקד, מדריך ומה שביניהם – חלק א – הקדמה
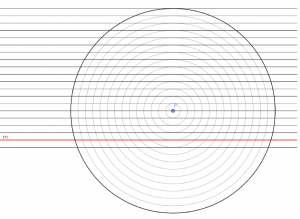
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
- סמנו בסרטוט לפחות 15 נקודות, שמרחקן מהנקודה F, שווה למרחקן מישר m.
- סמנו באות O את הנקודה הקרובה ביותר לישר m ושמרחקה מנקודה F, שווה למרחקה מישר m.
- שערו איזו צורה מתקבלת אם מחברים את כל הנקודות שסימנתם?
תוכלו להיעזר ביישומון המצורף.
- יש לגרור נקודות ממחסן הנקודות, אל המיקום המתאים.
- כדי למקם את הנקודות, ניתן להיעזר בסרגלי הגרירה:
- מספר המעגל.
- מספר הקו האופקי.
- לחצו על כפתור "בדיקה". נקודה שנמצאת במיקום המתאים תהפוך לירוקה, ונקודה שלא נמצאת במיקום המתאים תהפוך לאדומה.
- יש לבצע בדיקה מחודשת לאחר הזזת הנקודה למיקום אחר.
- ניתן להציג/להסתיר קווים אופקיים, מעגלים, ומשבצות.
פתרון בעיית מטרה 1
סעיף א
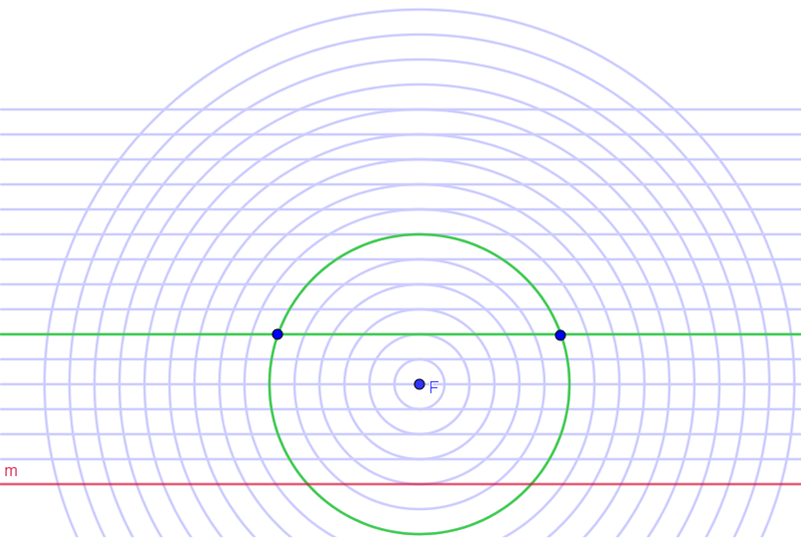
נקודות, הנמצאות במרחק שווה מנקודה F ומהישר m, נמצאות במפגש בין המעגל שמספרו n (רדיוסו n/2) לבין הקו האופקי שמספרו n (מרחקו מהמדריך n/2).
הנקודות, המסומנות בסרטוט, נמצאות על מעגל מספר 6.
במילים אחרות, הן במרחק 3 יחידות מ- F, ועל קו אופקי מספר 6.
כלומר, במרחק 3 יחידות מהישר m.
סעיף ב
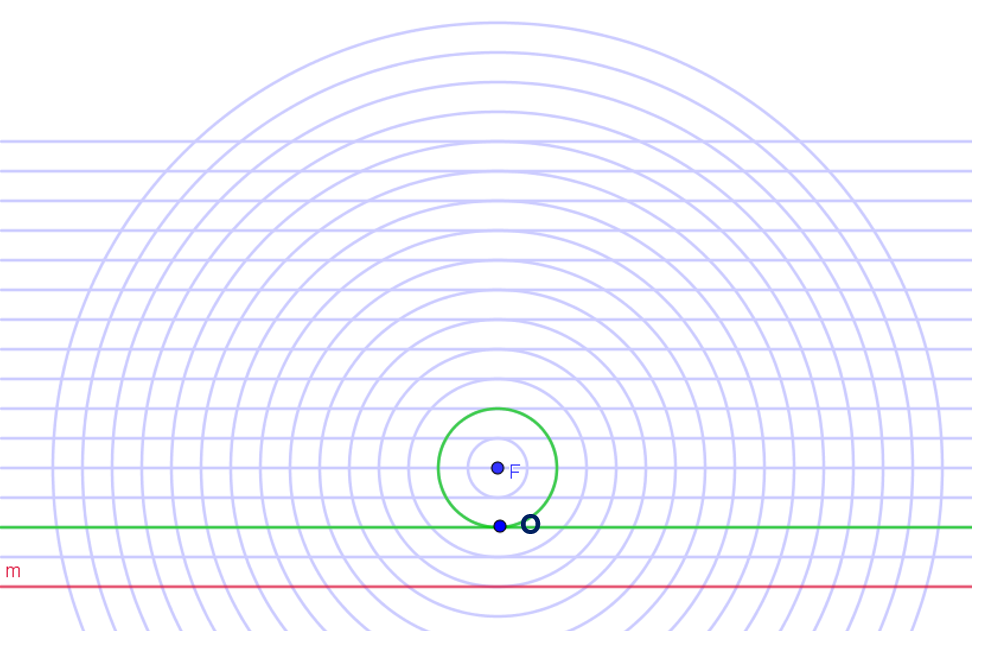
הנקודה הקרובה ביותר לישר m, שנמצאת במרחקים שווים מנקודה F ומישר m, נמצאת במפגש בין מעגל מספר 2 וקו אופקי מספר 2.
מרחקה מ- F ומהישר m שווה ליחידה אחת.
סעיף ג
הגרף המתקבל הוא פרבולה.
הערה:
הפעילות מובילה לתפיסה אינטואיטיבית בלבד של תכונת הפרבולה המובאת בסיכום.
בבעיית הסיכום (רשות) מגיעים התלמידים להוכחה כי הגרף המתקבל הוא פרבולה.
1.1 מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
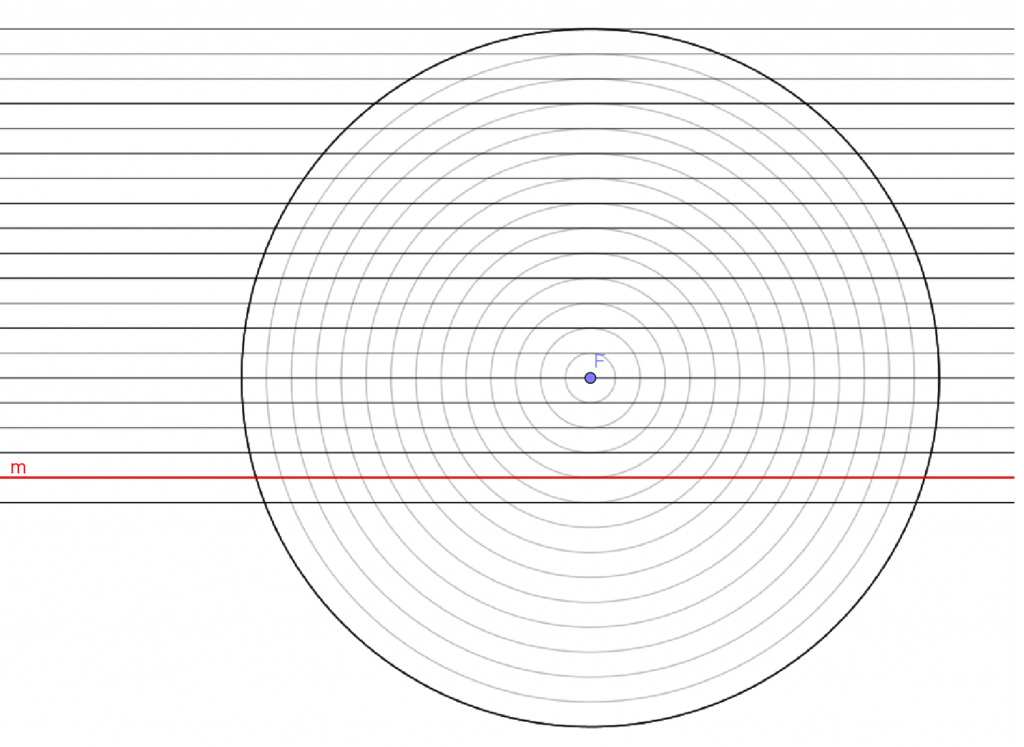
לכל המעגלים שבסרטוט מרכז משותף – נקודה F.
רדיוס המעגל הקטן 0.5 יחידה, רדיוס המעגל הבא אחריו 1 יחידה, וזה שאחריו 1.5 יחידות וכך הלאה.
המרחק בין הקווים האופקיים קבוע ושווה ל- 0.5 יחידה.
סמנו בסרטוט את שתי הנקודות שמרחקן מנקודה F ומרחקן מישר m הוא 4.5 יחידות.
תוכלו להיעזר ביישומון המצורף.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
- אחרי שפתרתם את השאלות במדרגה 1, חזרו לבעיית מטרה 1.
- או, במידת הצורך, פתרו את השאלות במדרגה 2.
- יש לגרור נקודות ממחסן הנקודות, אל המיקום המתאים.
- כדי למקם את הנקודות, ניתן להיעזר בסרגלי הגרירה:
- מספר המעגל.
- מספר הקו האופקי.
- לחצו על כפתור "בדיקה". נקודה שנמצאת במיקום המתאים תהפוך לירוקה, ונקודה שלא נמצאת במיקום המתאים תהפוך לאדומה.
- יש לבצע בדיקה מחודשת לאחר הזזת הנקודה למיקום אחר.
- ניתן להציג/להסתיר קווים אופקיים, מעגלים, ומשבצות.
פתרון מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
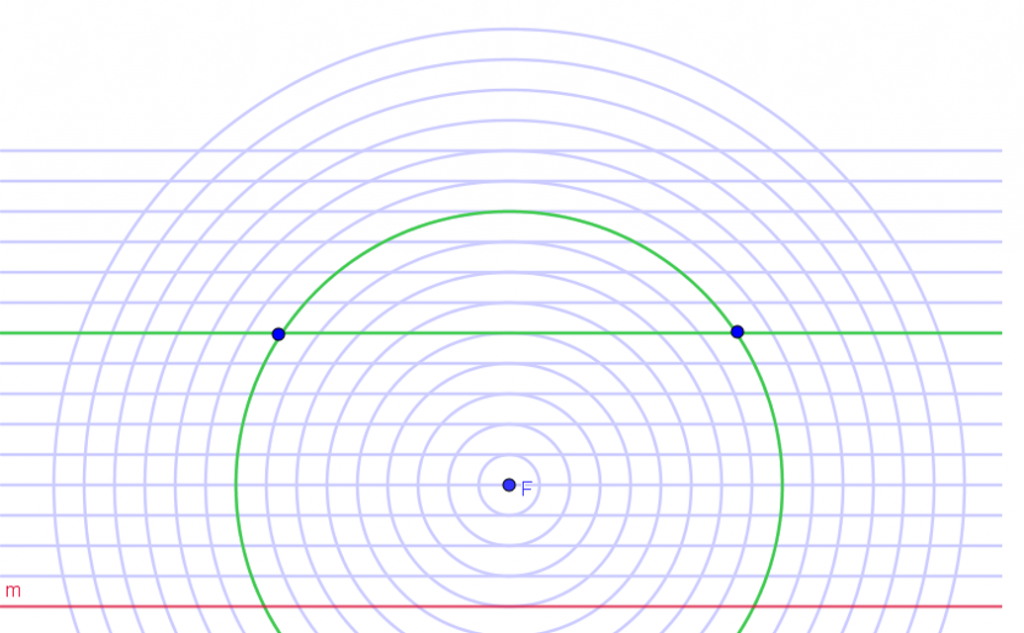
הנקודות, הנמצאות במרחק 4.5 יחידות מנקודה F ומישר m, נמצאות במפגש המעגל התשיעי והקו האופקי התשיעי.
ראו סרטוט מצורף.
מטרת מדרגה 1 לבעיית מטרה 1
בעיה 1.1.1
בבעיה יש לסמן רק שתי נקודות שמרחקן מנקודה F ומהישר m נתון.
הבעיה מאפשרת לתלמיד להתמקד במציאת נקודות מסוימות.
היא מאפשרת להבין שיש שתי נקודות הנמצאות במרחק מסוים מ-F ומהישר m, ומאפשרת להבין שאם המרחק המבוקש הוא 4.5, אזי הנקודות תמצאנה במפגש בין המעגל התשיעי והקו האופקי התשיעי.
1.2 מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
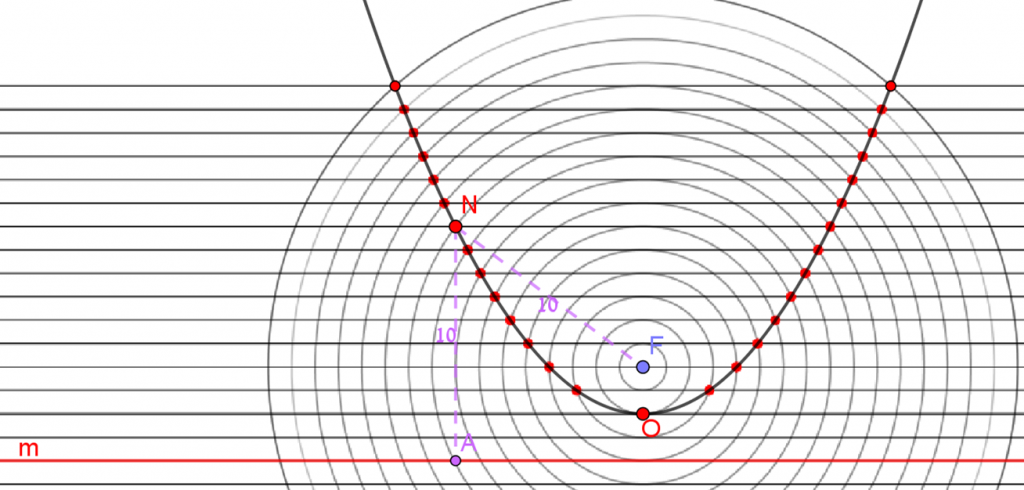
לכל המעגלים שבסרטוט מרכז משותף – נקודה F.
רדיוס המעגל הקטן הוא 0.5 יחידה, רדיוס המעגל הבא אחריו 1 יחידה, וזה שאחריו 1.5 יחידות וכך הלאה.
המרחק בין הקווים האופקיים קבוע ושווה ל- 0.5 יחידה.
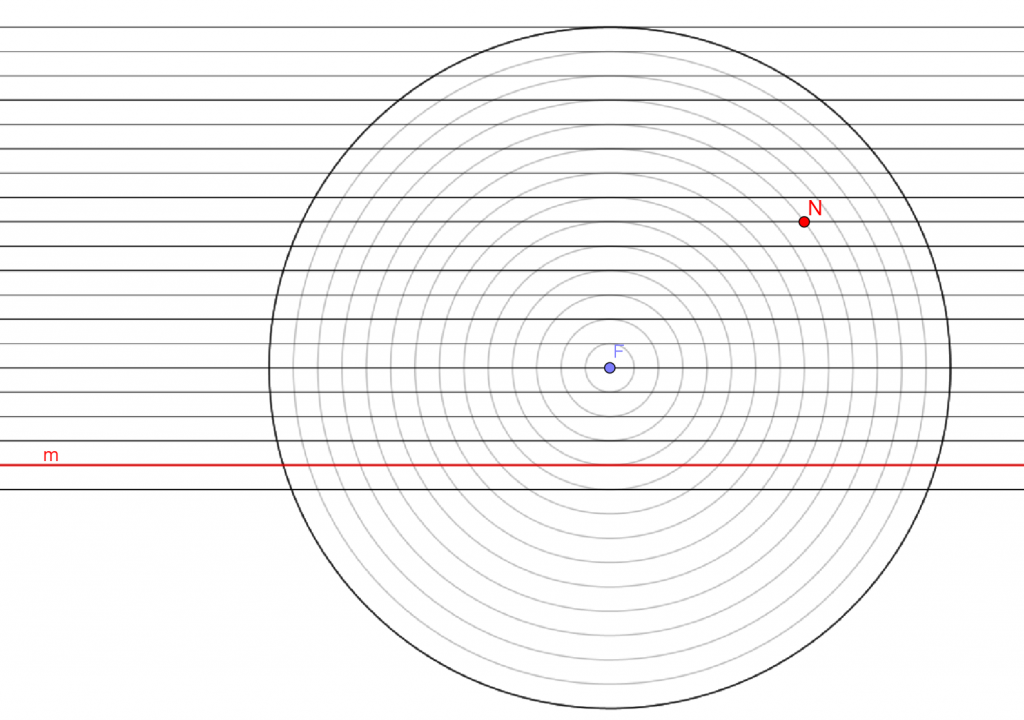
האם נכונה הטענה שהמרחק של נקודה N מנקודה F, שווה למרחק של נקודה N מישר m?
אם לא – נמקו, אם כן – מצאו למה שווה המרחק.
תוכלו להיעזר ביישומון המצורף.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
- אחרי שפתרתם את השאלות במדרגה 2, חזרו לבעיית מטרה 1.
- ניתן להיעזר בסרגלי הגרירה:
- מספר המעגל.
- מספר הקו האופקי.
- ניתן להציג/להסתיר קווים אופקיים, מעגלים, ומשבצות.
פתרון מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
נקודה N נמצאת במרחק שווה מנקודה F ומישר m.
היא נמצאת במפגש המעגל העשירי והקו האופקי העשירי,
ולכן המרחק הוא 5 יחידות.
מטרת מדרגה 2 לבעיית מטרה 1
בעיה 1.2.1
בבעיה נתונה נקודה מסוימת ויש לקבוע האם מרחקה מ- F שווה למרחקה מהישר m.
כדי לקבוע זאת, יש להבין כיצד להיעזר במעגלים ובקווים המקבילים לישר m.
הבנה זו מאפשרת למצוא נקודות נוספות, הנמצאות במרחק שווה מ- F ומ- m.
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
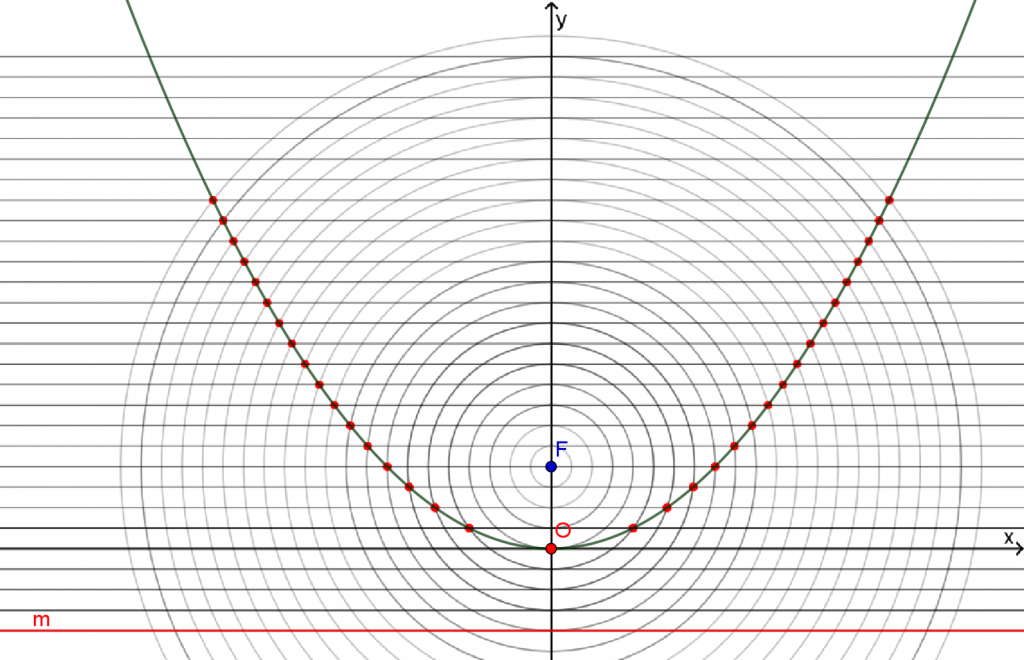
נוסיף מערכת צירים לסרטוט (לחצו על הכפתור "צירים" ביישומון),
כך שציר ה- x מקביל לישר m וראשית הצירים היא בנקודה O (הנקודה הקרובה ביותר לישר m ושמרחקה מנקודה F שווה למרחקה מישר m):
(ניתן ללחוץ על הסרטוט ולהגדיל אותו)
זוהי פרבולה (המוכרת לנו) שהביטוי האלגברי שלה הוא f(x)=ax2.
ראו יישומון מצורף.
- המשיכו לבעיית הסיכום (רשות).
- או, המשיכו להמשך הסיכום.
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.
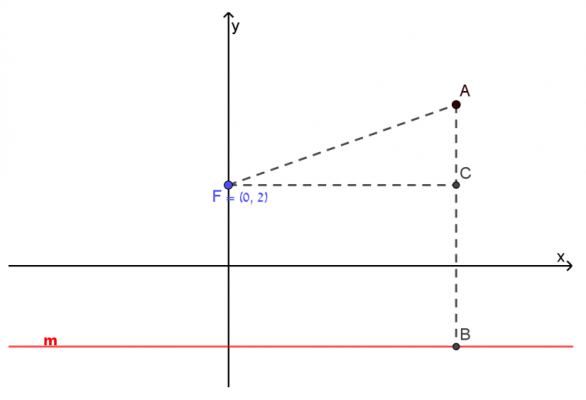
- בטאו את הקטעים AF ו- AC באמצעות yA. נמקו תשובתכם.
- הוכיחו כי: yA=18(xA)2
- מצאו את השיעורים של שלוש נקודות, שכל אחת מהן נמצאת במרחק שווה מנקודה F ומישר m.
- איזה גרף מתקבל מאוסף כל הנקודות שמרחקן מנקודה F שווה למרחקן מישר m?
נמקו תשובתכם.
- אחרי שפתרתם את בעיית הסיכום (רשות), המשיכו להמשך הסיכום.
פתרון בעיית הסיכום (רשות)
נתון כי:
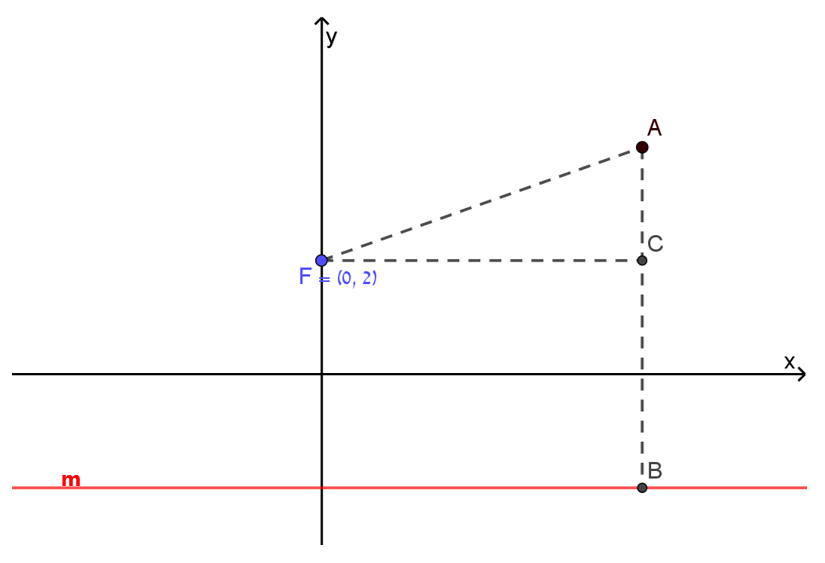
שיעורי נקודה F הם: (0,2), וישר m הוא הישר y=−2.
נקודה A היא נקודה כלשהי, שמרחקה מנקודה F, שווה למרחקה מישר m.
AB מרחק נקודה A מישר m.
נקודה C נמצאת על AB, כך שקטע FC מקביל לציר ה- x.
הוכחה
AC=yA−yC=yA−2
AB⊥m מרחק נקודה A מישר m
FA=AB=yA+2
FA2=AC2+FC2 משפט פיתגורס
(yA+2)2=(yA−2)2+(xA)2
(yA)2+4⋅yA+4=(yA)2−4⋅yA+4+(xA)2
yA=18(xA)2
- המשיכו למה עוד אפשר לשאול.
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.
- ניתן לגרור את הנקודה שעל הפרבולה, כדי לראות את המרחק מהמוקד (F) ומהמדריך (ישר m).
- לחצו על כפתור "צירים" כדי להציג/להסתיר את מערכת הצירים.
- ניתן להציג בעזרת סרגלי הגרירה את:
- מספר המעגל.
- מספר הקו האופקי.
- הערה: כשמוצגים גם מעגלים וגם קווים אופקיים, מוצגות גם נקודות החיתוך המתאימות שביניהם.